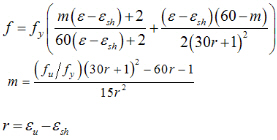This Kent and Park (1973) concrete model, which was modified by Scott, et al. (1982), can consider the Confinement Effect due to reinforcing and is rated highly because of its clear formation and accurate analysis.

	Concrete compressive cylinder strength
	Factor, which accounts for the strength increase due to confinement
	: Ratio of the volume of hoop reinforcement to the volume of concrete core measured to outside of stirrups      : Yield strength of stirrup steel
	Strain at compressive Crushing
	Strain at maximum compressive strength
	Strain softening slope - coefficient representing the stiffness in the concrete softening zone after compression yielding
	: Width of concrete core measured to outside of stirrups   Sh: Center to center spacing of stirrups or hoop sets

 

Note

can be obtained by the proposed equation of Scott et al, or another value may be used at user's discretion.

 In this model, the concrete tensile strength is ignored since it has little effect on the entire member.

Hysteresis characteristics of this model are as follows:

a. When a member is unloaded under compression, its behavior is represented by the line connecting   and ; where  is the strain at the beginning of unloading and  is a certain point on the strain axis. As the compression increases, the slope of this line becomes flatter. The relationship is defined as:

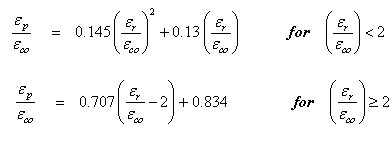
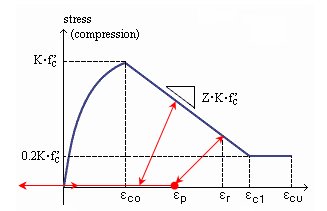
b. Tensile strength is ignored in this model. Therefore, under Complete Unloading or Open Crack, the stress becomes '0'(as shown in the above figure).

c. When reloaded, the stress values before attaining   shall be taken as '0'. Once the compressive strain exceeds, reloading is applied along the line where the unloading occurred. In reality, Unloading and Reloading cannot be applied linearly, since it is actually a nonlinear application. However since there is not much difference between linear and nonlinear behavior, the results will be accurate enough even if linear Unloading and Reloading is assumed

This model is presented in Seismic Performance Comparison Investigation, P23 of Japanese Concrete Standard Specification. Softening zone after the maximum stress, residual plastic deformation and stiffness reduction effect under the condition of reloading after unloading are reflected.

: Compressive strength of concrete cylinder

ε'peak: Strain at maximum compressive strength

This model is presented in Commentary V -Seismic Design (Concrete confined by reinforcing steel, p. 161) of Japanese Roadway Specification.

Earthquake Type I: Ultimate strain and the strain at maximum compressive strength are the same, and the zone of descending slope (Edes) does not exist.  

Earthquake Type II: Ultimate strain is calculated by the Specification, and the zone of descending slope (Edes) is retained.  

Ec: Young's Modulus of concrete

σck: Design strength of concrete

σsy: Yield point of confining reinforcing steel

α, β: Sectional modification coefficients

Note
For a circular section, α=1.0, β=1.0
For trapezoidal, hollow circular and hollow trapezoidal section, α=0.2, β=0.4

Ah: Cross-sectional area of a single confining rebar

s: Spacing of lateral confinement

d: Longer length of a concrete section dimension confined by main stirrups or local stirrups

σbt: Tensile strength of concrete

σcc: Strength of concrete confined by laterally restraining rebars

This model is presented in Seismic Performance Comparison Investigation p.7 -Structural steel pier partially filled with concrete of Nagoya Highway Corporation.  

σck: Compressive strength of concrete cylinder

εcc : Strain at maximum compressive strength

K: Coefficient to reflect the increase in compressive strength

εcu: Ultimate compressive strain of concrete

εt0: Strain at maximum tensile strength

εt1: Strain at tensile rupture of concrete

εtu: Ultimate tensile strain of concrete

Both tensile and compressive zones can be defined in this model. Trilinear hysteresis exists in the compression zone, which can be defined by the stress-strain relationship and the stress-stiffness reduction ratio relationship.  

σc1: First compression yielding of concrete

σc2: Second compression yielding of concrete

σc3: Stiffness of concrete after second compression yielding (required for K3 calculation)

ε: Strain at maximum tensile strength

εt1: Strain at tensile rupture of concrete

εtu: Ultimate tensile strain of concrete

εc1: Strain at first compression yielding of concrete

εc2: Strain at second compression yielding of concrete

εc3: Strain after second compression yielding (required for K3 calculation)

εcu: Strain at third compression yielding of concrete

K1: Initial stiffness of concrete

K2/K1: Ratio of stiffness after the first yielding to the initial stiffness

K3/K1: Ratio of stiffness after the second yielding to the initial stiffness

Note
When ε_c1~ε_c3 are entered in the 'σ - ε' input method, and the 'σ - α' input method is selected, K1, K2/K1, K3/K1 are automatically calculated. Also the reverse calculation is automatically done.

This is the concrete model confined by transverse rebar, which was suggested by Mander (1988). Transverse rebars are provided to confine core concrete, and to prevent buckling failure of main rebars and shear failure of the member. Compressive concrete confined by transverse rebar can increase strength and ductility of a member due to the confinement effect.

 Mander model provides the Stress-Strain relationship of the confined concrete, regardless of the section shape. Also the Effective Confined Stress can be obtained considering longitudinal rebar area, transverse rebar area, rebar strength, and rebar type. Mander model is based on the single-axis Stress-Strain curve, suggested by Popovic(1973). However, using Mander model, Effective Confined Stress of multi-axis can be transferred to that of a single-axis.

Concrete Type

 Unconfined Concrete : Select to define cover concrete. Confinement effect will not be considered and confinement   related options will be inactivated.

 Confined Concrete : Select to define core concrete confined by transverse rebar.

 

Unconfined Concrete Data

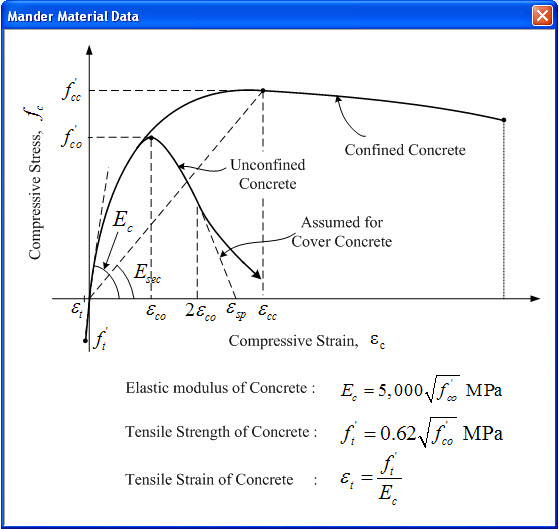
  Stress-Stiffness Reduction Ratio Definition

 

fco': Unconfined concrete strength. Select this optionto directly define the value of concrete strength.

εco: Unconfined concrete strain. Select this option to directly define the value of concrete strain.

Ec: Elastic modulus of concrete. When "Mander et al." is selected, it is automatically calculated. When "User Input" is selected, the user can directly enter the value.

ft': Tensile strength of concrete. When "Neglect Tensile Strength" is selected, tensile strength of concrete is ignored. When "Mander et al." is selected, it is automatically calculated. When "User Input" is selected, the user can directly enter the value.

εt: Tensile strain of concrete. It is automatically calculated based on the defined tensile strength.

 

 Section & Confinement Rebar Type

This option is activated when Concrete Type is defined as "Confined Concrete : Core Concrete". Define the section type and rebar type of the transverse rebar.  

  : Define the core concrete dimension and confinement rebar spacing, etc.

  : Define the longitudinal rebar and confinement rebar related data.

 

 Confinement Effective Coefficient, Ke

 Confinement effective coefficient of concrete that considers section size, rebar area, and rebar type.

 The Effective Lateral Confining Stress on the Concrete

 flx : Effective confining stress in the x-direction.

 fly : Effective confining stress in the y-direction.

 fl : Effective confining stress transferred from multi-axis to single-axis.

Confined Concrete Strength & Strain : Compressive concrete strength and strain considering confinement effect. Type your drop-down text here.

This is the steel model of Menegotto and Pinto, which was modified by Filippou et al.

fy: Yield strength of reinforcing steel

E: Modulus of elasticity

b: Stiffness reduction factor after yielding

Ro, a1, a2: Coefficients for shape index (R) for steel fiber constitutive model

This Stress-Strain hysteresis model is outlined as follows:

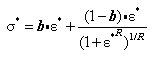
The above formula represents a curved transition from the elastic range to the yielding range.

and  are normalized values and are calculated as follows:

 

 

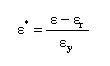
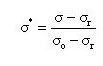
This model has two asymptotes as shown below. One asymptote has a slope of elastic stiffness and the other has a slope of yielding stiffness.  is a point intersected by two asymptotes.  is the point where the last unloading occurred. While unloading and reloading, these points are updated, so that the transition curve is affected.

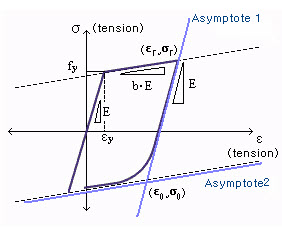
R is the value that can affect the shape of the transition curve and represents the Bauschinger effect. The value of R is determined as follows:

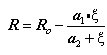
Coefficients  are determined from experimental hysteresis results. MIDAS uses 18.5, 0.15 and 20, respectively, as default values. These default values are suggested in the original reference (Menegotto and Pinto,1973).

is a shape coefficient and updated at every unloading.

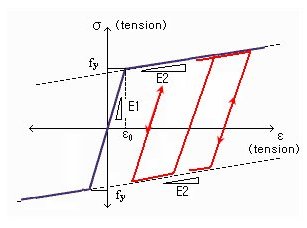
This model represents a general symmetric Bilinear model for reinforcing steel.

fy: Yield strength of reinforcing steel

E1: Initial stiffness of reinforcing steel

E2/E1: Ratio of stiffness after yielding to the initial stiffness

As shown in the figure below, the model behaves elastically when it is unloaded and reloaded after yielding.

 

This model has been derived from the general bilinear steel model. Stiffness after compressive and tensile yielding can be freely defined. Buckling and rupturing of reinforcing steel can be considered.

σy: Tensile yield strength

σcy: Compressive yield strength

ε1: Strain at compression buckling of reinforcing steel

ε2: Strain at rupturing of reinforcing steel after yielding

E1: Initial stiffness of reinforcing steel

E2: Stiffness of reinforcing steel after tensile yielding

E3: When tension becomes unloaded and reloaded in the compression zone, the E3 line limits the stiffness under compression loading.

E4: Stiffness of reinforcing steel after compressive yielding

 (A negative slope can be specified by entering a negative value.)

E5: Stiffness of buckled reinforcing steel after compressive yielding

This Model can describe compressive yielding, tensile yielding, tension rupture, compression buckling, etc of reinforcing steel. The figure below shows the possible hysteresis states.  

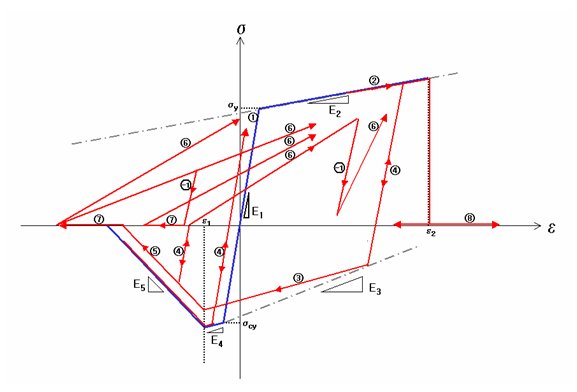
Each state is explained as follows:

Since tension behavior is the major cause of hysteresis in steel, the loading direction basically follows tension. During unloading, the loading direction changes from tension to compression, and vice-versa during reloading.

State 1: It represents the elastic behavior, and the slope is E1.

1 → 2 = Transition to yielding state. The slope is E2 under tensile yielding and E4 under compressive yielding.

State 2: It represents the state after the yielding starts, and the slope is E2.

2 → 4 = Unload and reload after yielding.

2 → 8 = Tension is sustained after yielding, and thereafter, tension rupture is caused. The stress is always '0' after the rupture.

State 3:  Unload continuously and as a result the compression zone yields. The slope is E2. E3 should be input such that the point intersecting the line E3 and strain axis is greater than .

3 → 4 = Reload. The slope is E1.

3 → 5 = As unloading continues, the compression strain exceeds  and compression buckling starts. The slope is E5.

State 4: Unloading and reloading with slope E1 (elastic stiffness)

4 → 2 = As reloading continues, the state changes to tensile yielding state. Or as unloading continues, the state changes to compressive yielding state.

4 → 3 = As unloading continues, compressive yielding occurs. It can be assumed that compressive yielding occurs at the intersection with line E3.

4 → 5 = As unloading continues, compression buckling starts.  

State 5: When compression strain exceeds buckling strain, buckling of reinforcing steel takes place. The slope is E5.

5 → 4 = Reloading continues during compression buckling.

5 → 7 = As compression is sustained, the reinforcing steel undergoes complete compression buckling. The stress becomes '0' at compression during and after State 7.

State 6: Reload after compression buckling. Reloading will progress towards before tensile yielding occurs. Reloading will progress towards the maximum point in the tension zone after tensile yielding occurs.    

6 → 2 = As reloading continues, tensile yielding takes place.

6 →-1 = Unload while reloading.

State 7: Once complete compression buckling occurs, further compressive stresses cannot be generated. Although compressive stress becomes '0' it can still resist tension.

7 → 6 = Reloading occurs and progresses towards the maximum tension point.

State 8: Once tension rupture occurs, further tensile stresses cannot be generated, and neither will compressive stresses be generated.

State ?: Unload while reloading after compression buckling (State 6). The slope is E1 (elastic stiffness).

 -1 → 6 = Reloading progresses towards the maximum tension point.

-1 → 7 = Unloading and the subsequent transition to complete compression buckling

As stated above, this model considers the various states and transitions. If the user is familiar with this model and applies the experimental parameters properly, it can be a very efficient tool. However, the user must use caution when using this model for limit states, such as tension rupture and compression buckling, as the resistance becomes '0'.   

This model represents a Trilinear model of three slopes.  The hysteresis can be defined by the stress-strain relationship and the stress-stiffness reduction ratio relationship.

When unloading and reloading, the model behaves elastically.                                            

σ1y: First yield strength in tension

σ2y: Second yield strength in tension

σ3y: Stiffness after second tensile yielding (required for K3 calculation)

σ'1y: First yield strength in compression

σ'2y: Second yield strength in compression

σ'3y: Stiffness after second compressive yielding (required for K5 calculation)

ε1y: Strain at first yielding in tension

ε2y: Strain at second yielding in tension

ε3y: Strain after second tensile yielding (required for K3 calculation)

ε'1y: Strain at first yielding in compression

ε'2y: Strain at second yielding in compression

ε'3y: Strain after second compressive yielding (required for K5 calculation)

K: Initial stiffness of reinforcing steel

K2/K1: Ratio of stiffness after first tensile yielding to the initial stiffness

K3/K1: Ratio of stiffness after second tensile yielding to the initial stiffness

K4/K1: Ratio of stiffness after first compressive yielding to the initial stiffness

K5/K1: Ratio of stiffness after second compressive yielding to the initial stiffness

Note
When ε1y~ε'3y are entered in the 'σ - ε' input method, and the 'σ - α' input method is selected, K1, K2/K1, K3/K1, etc. are automatically calculated. Also the reverse calculation is automatically done.

 

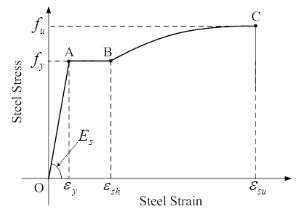
This model is proposed by Kent and Park (1973) followed by their experiments of cyclic loading on mild steel.  In this model,

elastic and plastic characteristics and strain hardening  can be manipulated. Bauschinger Effect is well described by the

Ramberg-Osgood equation and the results match relatively well with experimental results.                                           

fy: yield strength

fu: ultimate strength

Es: Elastic Modulus

εy: Elastic strain (at yield)

εsh: Strain at onset of hardening

εsu: Strain at failure

Case 1 : Behavior under loading

Behavior under loading is classified as follows. Thomson & Park's equation is applied in the relationship of stress and strain.

Stress-Strain curve for steel with loading of the same sign

Elastic Region (O-A): Plastic Region (A-B): Strain Hardening Region (B-C): ε : Steel strain f : Steel stress fy : Yield stress fu : Ultimate stress Es : Modulus of elasticity εy : Elastic strain at yielding εsh : Strain at the beginning of strain-hardening εsu : Ultimate strain at failure

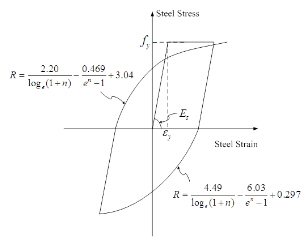
Case 2 : Behavior under unloading and re-loading

Behavior under cyclic loading is defined by the Ramberg-Osgood relationship and stress is computed with repetitive calculations of Newton's method.

Stress-Strain curve for steel with reversed loading

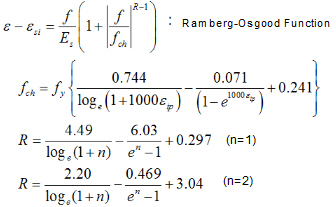
fch : Stress of Ramberg-Osgood function εip :Plastic strain of previous loading step (0 < εip < 0.7097) R : Ramberg-Osgood Parameter n : Loading Run Number     (Where, n=1 in compression, n=2 in tension) εsi : Strain of reinforcing steel when stress = 0 at loading