Integral Bridge Spring Supports

An integral bridge is one in which the bridge deck and its supporting abutments and piers are integrated without expansion joints to absorb the deformation of the bridge deck using the flexibility of the abutments and piers.

The prime concern in integral bridges is the effects of temperature variations on the deformation of bridge deck. Expansion and contraction of the bridge deck affects the backfill soil adjacent to the abutments. Backfill compaction due to a deck expansion and soil slide due to a deck contraction is repeated. Due to the repeated backfill compaction and soil slide, the modulus of subgrade reaction and the pressure distribution of backfill vary with depth.

A Cycle is the period from a deck expansion to a deck contraction. If cycles are repeated infinitely, the modulus of subgrade reaction of backfill becomes constant. Using the formulation proposed by B.M. Lehane, soil springs can be assigned.

To account for this characteristic of the soil, lateral springs are modeled as compression-only springs and vertical springs are modeled as linear elastic springs.

From the Main Menu select Boundary > Spring Supports > Integral Bridge.

Abutment Spring

Springs are automatically assigned to backfill and foundations. Backfill soil is defined as compression-only springs () and foundations are defined as linear elastic springs (). Entered data can be checked from Point Spring Supports Table.

Elements of Abutment

Direction: Select the direction in which Elastic Links are to be assigned.

Element List: Select the abutment elements to which backfill soil springs are to be assigned.

For beam elements to be assigned with springs, only Solid Rectangle ( ) and Box ( ) sections are applicable.
If Beta Angle is used for the abutment beam element, the width of the abutment is calculated based on the projection length ( ). This is identically applicable to the Footing.

Select Nodes for Footings

Select the nodes to which foundation springs are to be assigned.
Nodes for footings should be on a straight line.
If the nodes on a straight line are not continuous, select only the continuous nodes (at least two nodes) at a time.

When Solid elements are used, the nodes for footings should be located along the centerline of the abutment/footing width. As shown in the figure below, the blue nodes should be selected.

Geometry Data

Abutment Height (H)

Abutment Width (B)

Deck Length (L): Deck length along the longitudinal direction

Soil Parameter

Void Ratio (e): Ratio of void to backfill soil

Specific Gravity (Gs): The density of backfill soil. In general, 2.65.

Cycle factor (fcyc): This factor is assessed at about 2 based on the test conducted by [Cosgrove et al (2001)]. And this incorporates the reduction in void ratio brought about by cycling. Deck is expanded and contracted due to temperature variations. Integrated abutment is also deformed together. This is a factor used in the empirical formula which accounts for the state after infinite cycles.

Thermal Extension

Differential Deck Temp.: Temperature increment of deck

α: Thermal expansion coefficient of deck

Strip Footing Spring Data

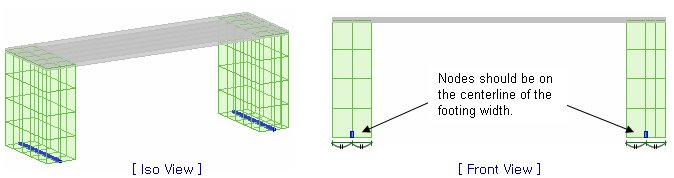
Found. Width (W): The width of foundation

Found. Bearing Pressure (p'): Foundation bearing pressure

Rot. Spring Dir.: Rotational direction of the foundation. If the longitudinal direction of the foundation is y, select Ry.

Computation of Stiffness of Compression-only Springs for Abutment Backfill

Stiffness per Unit Area
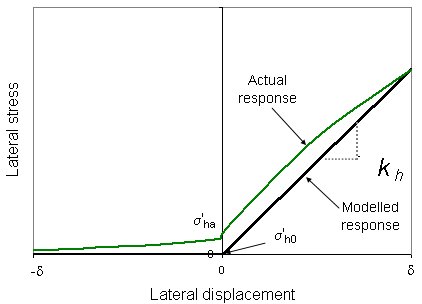
According to Broms (1971), the lateral stress-displacement relationship for abutment backfill of Integral Bridge is determined as shown in the figure above. The stiffness per unit area is calculated as follows:

Spring Stiffness
The final spring stiffness is determined by multiplying the stiffness per unit area by the area.

Computation of Stiffness of Linear Elastic Springs for Foundation

Stiffness per Unit Area

Spring Stiffness
The final spring stiffness is determined by multiplying the stiffness per unit area by the area.

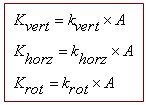
Pile Spring

Assign the springs for the soils adjacent to piles. Lateral springs for the soils adjacent to piles are modeled as symmetric nonlinear elastic springs () and vertical springs for the soils adjacent to piles are modeled as linear elastic springs ().

The stiffness of soil springs is automatically calculated and entered into Point Spring Supports. The entered data can be checked from Point Spring Supports Table.

Pile Spring Data

Select the frame element to which the pile springs have to be assigned.

Soil Type: Soil Types are classified into Sand / Soft Clay / Stiff Clay. Depending upon the selected Soil Type, stiffness calculation method will be different. Methods of calculating spring stiffness are explained at the bottom.

Ground Level: Z coordinate of ground

Pile Diameter (D)

Unit Weight of Soil (γ)

Earth Pressure Coeff. at rest (K0): Coefficient of earth pressure at rest

Coeff. of Subgrade Reaction (Kh): Modulus of subgrade reaction

Internal Friction Angle (Φ): Angle of internal friction of soil

Initial Soil Modulus (k1): Constant determined according to the relative density. Determines the stiffness of nonlinear elastic lateral springs for the soils adjacent to piles. Refer to Computation of Points k and m shown below.

Note

The elements to which the pile springs are assigned should have their local axis aligned in the same direction.

The Stiffness of Nonlinear Elastic (Lateral) Springs for the Soils adjacent to Piles

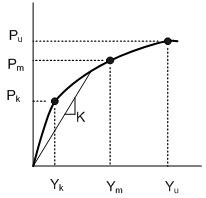
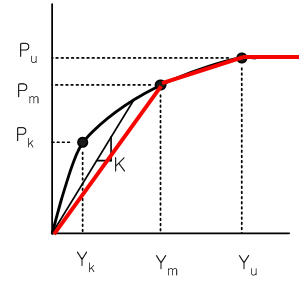
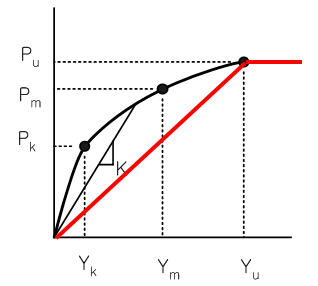
The relationship between the lateral soil resistance and the lateral displacement Y at a specific depth X is represented as shown in the left figure.

The values of Pk, Pm, Pu, Yk, Ym and Yu are defined at a specific depth (i.e., where pile springs are).

The method of calculating Pu varies with Soil Types. The values of Pk, Pm, Yk, Ym and Yu are calculated using Pu as explained below.

The calculation method is divided into two major cases - Sand and Clay. Different J values are used for Soft Clay and Stiff Clay, respectively.

Calculation of Pu in case of Sand Soil
The value of Xt denotes the depth when the following two Pu values are equal. Make the right terms of two equations equal, rearrange the equation in terms of X and solve the quadratic equation

Calculation of Pu in case of Clay Soil

Computation of Points k and m

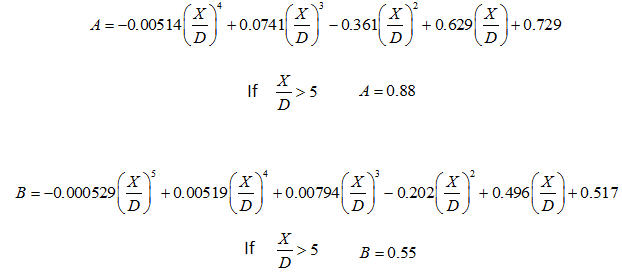
Note

If Yk is greater than Ym and less than Yu, the p-y curve will be tri-linear as shown below.

If Yk is greater than Yu, the p-y curve will be bi-linear as shown below.

Spring Stiffness
The final spring stiffness is determined by multiplying the stiffness per unit area calculated above by the area.

The Stiffness of Linear Elastic (Vertical) Springs for the Soils adjacent to Piles

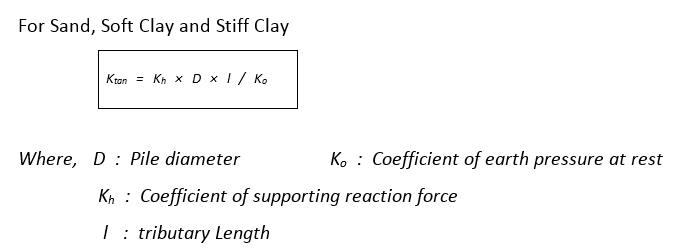
The direction of the linear elastic vertical springs for the soils adjacent to piles should be perpendicular to the ground (GCS '-'Z direction). Even though the piles are not perpendicular to the ground, the z-direction (Node Local Axis) of the nodes for Piles should coincide with the GCS Z-direction.