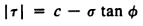Plastic Material

Specify a plastic material model for material nonlinear analysis.

 Plastic Material Models

1. 1. •  Tresca & Von Mises

Appropriate for ductile metals, which exhibit Plastic Incompressibility

• Mohr-Coulomb, Drucker-Prager

Appropriate for brittle materials such as concrete, rock and soils, which exhibit the behavior of volumetric plastic straining

• Masonry

Appropriate for the elastic analysis finding the crack positions using masonry walls (solid elements).

Note
Masonry material model is applicable to plate, 4-node solid, 6-node solid, and 8-node solid elements.

From the Main Menu select Properties > Plastic > Plastic Material.

For new or additional material properties

Click in the Plastic Material dialog box and enter the following data:

 Name: Name of plastic model

  Model: Type of plastic model

Tresca: This yield criterion is suitable for ductile materials such as metals, which exhibit Plastic Incompressibility.

Von Mises:This yield criterion is based on distortional strain energy and is the most widely used yield criterion for metallic materials.

Mohr-Coulomb:This yield criterion is a generalization of the Coulomb's friction rule and is suitable for materials such as concrete, rock and   soils, which exhibit volumetric plastic deformations.

Drucker-Prager:This criterion is a smooth approximation of the Mohr- Coulomb criterion and is an expansion of the von Mises criterion. This Drucker-Prager criterion is suitable for materials such as concrete, rock and soils, which exhibit volumetric plastic deformations.

Note

For additional details on the above 4 plastic models, refer to "Material Nonlinear Analysis" in the analysis manual.

Masonry: This model is suitable for the elastic analysis finding the crack positions using masonry materials such as bricks, mortar joints, etc.

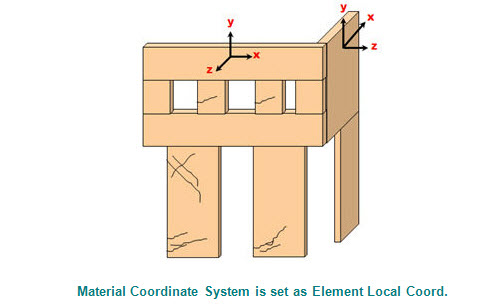
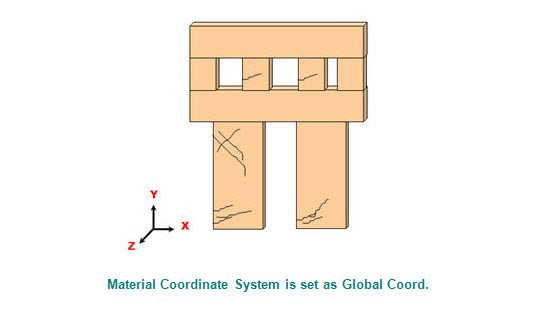
Note Material Coordinate System for Masonry models

Stress resultant beam model

• Stress resultant beam model is introduced to apply beam elements in the material nonlinear analysis. Thus, not only plate elements but also beam elements can be used for the analysis in which both geometric nonlinear effect and material nonlinear effect need to be taken into account. This feature would be useful for the nonlinear stability analysis of U-frame steel bridges which are often simulated using both beam elements and plate elements to represent cross beams and main girders, respectively

• The von-Mises yield criterion is used as the basis of the model.

• The stress-strain curve is linear elastic/perfectly plastic (i.e. zero hardening).

• Plastic axial force and plastic bending moment about major axis and minor axis are only calculated.

• The coupled effect between axial force and moment is not considered.

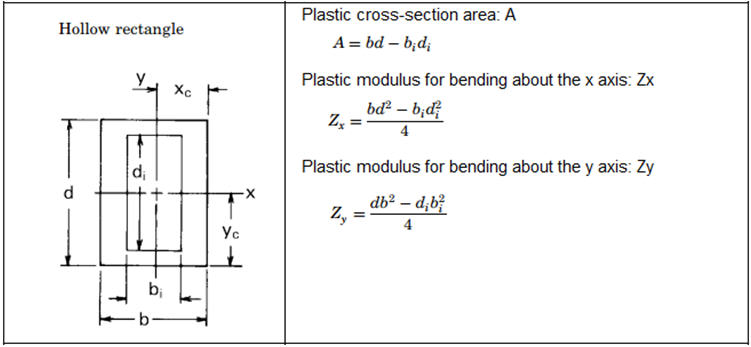
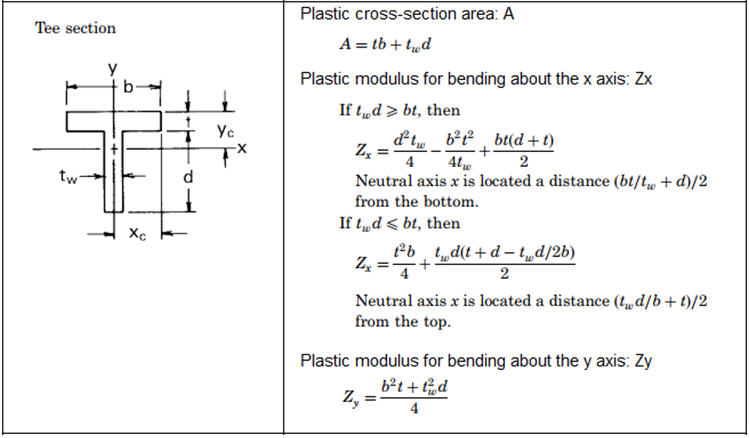
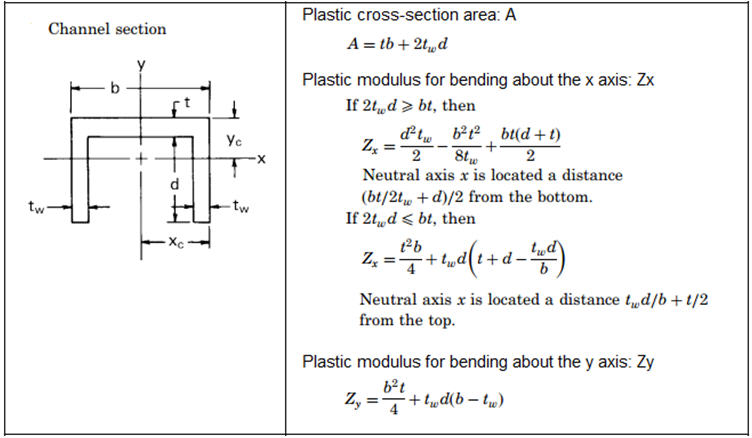
• Non-composite steel section is only supported. (Channel, I-Section, T-Section, Box, Pipe, Rectangle, Round section only.)

[Plastic Section Properties of Beam Model]     

Plastic Data

If Tresca or Von Mises is selected, specify Initial Uniaxial (tensile) Yield Stress.

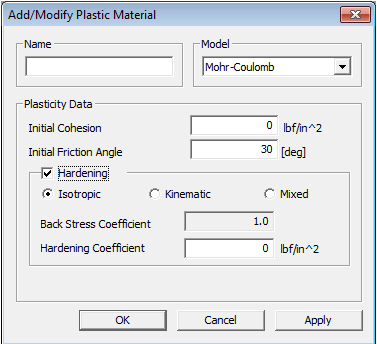
If Mohr-Coulomb or Drucker-Prager is selected, specify Initial Cohesion and Initial Friction Angle.

Initial Cohesion

Note

When normal stress is '0', Initial Cohesion is equal to the yield stress due to shear stress only.

Initial Friction Angle

Note

Initial Friction Angle, which is available only if Mohr-Coulomb or Drucker-Prager is selected as the Plastic Material Model, ranges from 0 to 90. Either use the default angle of 30 or specify the angle.

Hardening
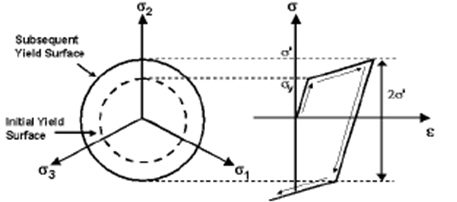
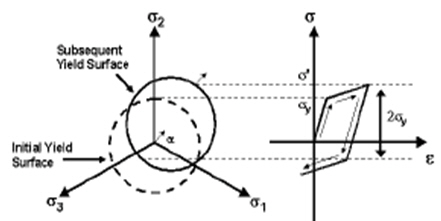
As a material yields, hardening defines the change of yield surface with plastic straining, which is classified into the following three types.

Isotropic: Isotropic hardening

Kinematic: Kinematic hardening

Mixed: Mixed type hardening

Note

For additional details on the above 3 hardening criteria, refer to "Material Nonlinear Analysis" in analysis manual.

Back Stress Coefficient
Represents the extent of Hardening

'1' for Isotropic Hardening
'0' for Kinematic Hardening
between '0~1' for Mixed Hardening

Note
Total increment of Plastic can be expressed by Isotropic Hardening and Kinemetic Hardening as follows:

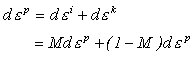
In this case, M here referred to as Back Stress Coefficient ranges between 0 and 1.

Hardening Coefficient
Tangent stiffness of material after yielding

Note

In case of von Mises model (Plastic Material), the Hardening Coefficient cannot exceed the Elastic Modulus defined in Model > Property > Material.

When Masonry is selected

Brick Material Properties

Bed Joint Material Properties

Head Joint Material Properties

Geometry of Masonry Panel

Revision of Civil 2015 (v1.1)

Q1. How can you simulate nonlinear behavior of concrete with plate / solid elements ?