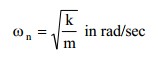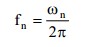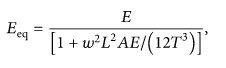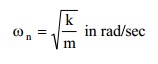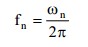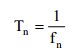Eigenvalue Analysis Control
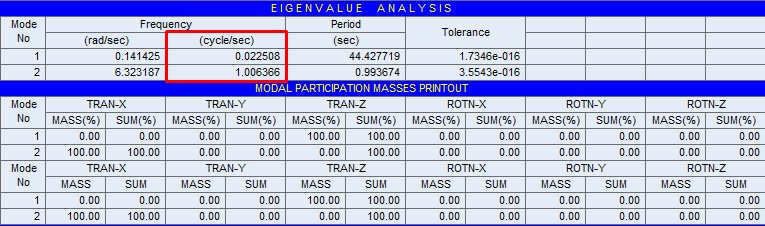
Eigenvalue analysis provides dynamic properties of a structure by solving the characteristic equation composed of mass matrix and stiffness matrix. The dynamic properties include natural modes (or mode shapes), natural periods (or frequencies) and modal participation factors.
1. Natural mode: A natural mode pertains to free vibration in an undamped system. 1st mode, 2nd mode and nth mode represent the order in which least energy is required to deform the structure.
2. Natural Period: A natural period is the time that it takes to freely vibrate the structure into the corresponding natural mode one full cycle.
3. Modal Participation Factor: The ratio of the influence of a specific mode to the total modes.
Enter the control data for the eigenvalue analysis.
midas Civil follows the procedure noted below for an eigenvalue analysis.
1. The self weight of the elements in the structure is converted into mass in Structure Type. Masses, which are not included in the model, can be entered by using the Loads to Masses conversion or by directly specifying Nodal Masses. Total mass can be checked in Mass Summary Table. Enter the mass data of the model using the various mass defining functions in the Load> Masses menu.
2. Invoke the Analysis > Eigenvalue Analysis Control menu and specify all the required data for performing eigenvalue analysis including the number of modes.
3. Select the Analysis > Perform Analysis menu or click 
Perform Analysis to carry out the analysis.
4. Once the structural analysis is successfully completed, use either the Results > Vibration Mode Shapes function or the Results > Result Tables > Vibration Mode Shape function to review various vibration mode shapes and eigenvalue mode frequencies or periods.
Note1
Tension-only/Compression-only element will be changed to Truss element in eigenvalue Analysis.
Note2
Eigenvalue analyses must precede dynamic analyses such as Time history analysis or Response spectrum analysis.
The response spectrum analysis uses the natural periods from the eigenvalue analysis. Thus, the entered spectral data must include the expected range of natural periods.
Note
Use the Load > Static Loads > Loads to Masses function to convert the desired static load data to nodal mass data. The conversion function may become quite useful when we try to apply the dead load already entered to the mass data required for a seismic analysis. In case DOF of the nodes to which nodal masses have been assigned are constrained, the corresponding masses are included in the total mass, but excluded from the effective mass. Therefore, the user must not constrain the DOF of the nodes assigned with masses when checking mass modal participation factors.
From the Main Menu select Analysis > Analysis Control > Eigenvalue.
Type of Analysis
Eigen Vectors
Subspace Iteration
pace Iteration matrix calculation is used to perform eigenvalue analysis. This method is effectively used when performing eigenvalue analysis for a finite element system of a large scale (large matrix system) and commonly used among engineers.
Lanczos
Tridiagonal Matrix is used to perform eigenvalue analysis. This method is effectively used when performing eigenvalue analysis for lower modes.
Ritz Vectors
Unlike the natural eigenvalue modes, load dependent Ritz vectors produce more reliable results in dynamic analyses with relatively fewer modes. The Ritz Vectors are generated reflecting the spatial distribution or the characteristics of the dynamic loading.
.jpg){kind=small}
If Eigen Vectors is selected
Subspace Iteration
Subspace Iteration matrix calculation is used to perform eigenvalue analysis. This method is effectively used when performing eigenvalue analysis for a finite element system of a large scale (large matrix system) and commonly used among engineers.
Lanczos
Tridiagonal Matrix is used to perform eigenvalue analysis. This method is effectively used when performing eigenvalue analysis for lower modes.
Eigen Vectors
Number of Frequencies
Enter the number of natural frequencies to be computed. If the Number of Frequencies entered exceeds the maximum number of vibration mode shapes that the structure can have, the program automatically performs analysis with the maximum number of vibration mode shapes.
Appropriate number of frequencies can be checked by the sum of modal participation factors (or accumulated mass participation ratios). The mass participation ratio represents the ratio of the sum of effective masses corresponding to a mode to the total mass. In general, most influential modes are considered to have been reflected if the sum of mass participation factors is above 90%. If the sum of mass participation factors is less than the required level, the user must increase the number of modes.
Frequency range of interest
Set the range of structure's frequencies to be computed from a minimum to a maximum.
The computation starts from the set Lower Frequency, and the Frequencies are computed within the set range. If the computed natural frequency turns out to be larger than the set Upper Frequency, no additional frequencies are calculated. Only the values smaller than the Upper Frequency are used in the ensuing analysis.
Search From: Minimum frequency in the range
Search To: Maximum frequency in the range
Eigenvalue Control Parameters
Enter the maximum number of iterations, the subspace size and the convergence tolerance. These parameters are necessary when the Subspace Iteration method is used for Eigenvalue analysis.
The Subspace Iteration Method is used for Eigenvalue analysis in MIDAS/Civil. The iteration continues until the relative frequency,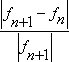 
, calculated does not exceed the convergence tolerance.
If the relative natural frequencies are not within the convergence tolerance after the maximum number of iterations is exhausted, no additional calculation is performed and the previously calculated natural frequencies are used for the subsequent tasks.
Eigenvalue analysis and Buckling Analysis may not be performed simultaneously. Eigenvalue analyses must precede dynamic analyses such as Time history analysis or Response spectrum analysis.
The response spectrum analysis uses the natural periods from the Eigenvalue analysis. Thus, the entered spectral data must include the expected range of natural periods.
Number of Iteration: Enter the maximum number of iterations.
Subspace Dimension: Enter the subspace size.
Convergence Tolerance: Enter the convergence tolerance. In general, 1e-10.
The Subspace Iteration Method is used for Eigenvalue analysis in MIDAS/Civil. The iteration continues until the relative frequency, |fn+1-fn| / |fn+1|, calculated does not exceed the convergence tolerance.
If the relative natural frequencies are not within the convergence tolerance after the maximum number of iterations is exhausted, no additional calculation is performed and the previously calculated natural frequencies are used for the subsequent tasks.
Sturm Sequence Check
Check to detect any missed eigenvalues. The Sturm sequence check can be used to obtain all the eigenvalues from the lower modes without any lost modes.
If Ritz Vectors is selected
Ritz Vectors
Unlike the natural eigenvalue modes, load dependent Ritz vectors produce more reliable results in dynamic analyses with relatively fewer modes. The Ritz Vectors are generated reflecting the spatial distribution or the characteristics of the dynamic loading.
Starting Load Vectors
Specify a desired load case, which will be used to generate the initial vectors, to calculate the Ritz Vectors. The load case may be a static load or inertia forces in each direction. Specify a desired number of load cases to generate Staring Load Vectors to calculate the Ritz Vectors. The load cases may be in the form of a static load and a ground acceleration load.
Number of Generations
Specify the number of Ritz Vectors to be generated for each starting load vector.
.jpg){kind=small}
: Enter the selected load case to calculate the starting load vector.
.jpg){kind=small}
: Modify the entered load condition.
.jpg){kind=small}
: Delete the previously entered load condition.
Note
For example, when the loading is considered in the X-direction, a 5-story building can have a maximum of 5 starting load vectors.
Include GL-Link Force Vectors
The loads that cause the deformations of general link elements are automatically included to calculate the starting load vectors. It is intended to reflect the modes related to the deformations of general link elements in an analysis using general link elements.
Number of GL-Link Force Vectors
The program examines and produces the number of starting load vectors created by the entered general link elements.
Number of Generations for Each GL-link Force
Enter the number of Ritz Vectors to be generated for each GL-link load.
Total Number of Starting Load Vectors
The number of total starting load vectors, which are used to calculate the Ritz Vectors, is indicated.
Total Number of Ritz Vectors
The total number of Ritz Vectors, which are created by individual starting load vectors, is indicated.
In the case where a number of Ritz vectors defined by the user for one load case cannot be calculated, the deficient modes are calculated based on other load cases selected in the sequential order. The order follows the sequence of the load cases entered by the user. When the number of Ritz Vectors calculated is still less than the number of modes specified by the user even after the adoption of other load cases, only the calculated modes are used to carry out the subsequent dynamic analyses.
To delete all the entered data, click .jpg){kind=small}
.
