Tendon Property
Define the tendon properties such as tendon area and instantaneous prestress losses.
From the Main Menu select Load > Temp/Prestress > Tendon Property.
![]() To define new or additional tendon properties
To define new or additional tendon properties
Click ![]() in the Tendon
Property dialog box and enter the following:
in the Tendon
Property dialog box and enter the following:
 Tendon Name:
tendon name being defined
Tendon Name:
tendon name being defined
 Tendon Type
Tendon Type
Define the tendon type among Pre-Tension, Post-Tension and External.
Internal (Pre-Tension): Prestressing tendons prior to casting concrete, which transmits prestress through bonding between concrete and tendons
Internal (Post-Tension): Post-tensioning tendons through hardened concrete members - tendons are gradually stressed and anchored to the members.
External: Tendons are placed external to concrete members and stressed.
Note 1
Depending on the Tendon Type (Pre-Tension,
Post-Tension and External), the
entry fields for variables related to tension losses in tendons
and duct diameter are either activated or inactivated.
Note 2
If the tendon placement location is External, the tendon is displayed
as a straight line in .jpg) Display.
Display.
 Material
Material
Select the material
properties of the tendon. Click ![]() to the right
to add new or modify/delete previously defined tendon properties.
For pre-tension type tendon, consider the elastic deformation
loss due to axial force and moment acting on the tendon.
to the right
to add new or modify/delete previously defined tendon properties.
For pre-tension type tendon, consider the elastic deformation
loss due to axial force and moment acting on the tendon.
Note
Weight density of tendon is not taken into account in the calculation
of self weight because tendon is considered as equivalent loads
rather than elements. In practice, the self weight of reinforcement
including tendons is taken into account by increasing weight density
of concrete.
 Total Tendon Area
Total Tendon Area
Specify the total
area of the tendon. You may either directly specify the cross-sectional
area or click ![]() to enter
the standard cross-sectional area and the number of strands for
auto-calculation of the total area.
to enter
the standard cross-sectional area and the number of strands for
auto-calculation of the total area.
|
Tendon Type |
|||||
12. 4 |
12. 7B |
15. 2B |
G15. 2 |
28. 6 |
||
Number of Strands |
EA |
12 |
12 |
12 |
19 |
1 |
Tendon Area |
CM2 |
11.148 |
11.8452 |
16.644 |
26.353 |
5.324 |
Duct Diameter |
CM |
6.8 |
6.8 |
7.8 |
11.5 |
5 |
Wobble Friction Factor λ |
/m |
0.004 |
0.004 |
0.004 |
0 |
0.004 |
Curvature Friction Factor μ |
/rad |
0.3 |
0.3 |
0.3 |
0.3 |
0.3 |
Anchorage Slip |
mm |
11 |
12 |
11 |
5 |
5 |
Relaxation |
% |
5 |
5 |
5 |
1.5 |
2.5 |
Young's Modulus |
N/mm2 |
200000 |
200000 |
200000 |
200000 |
200000 |
Yield Strength σpy |
N/mm2 |
1450 |
1600 |
1600 |
1600 |
1500 |
Tensile Strength σpu |
N/mm2 |
1700 |
1850 |
1850 |
1860 |
1800 |
 Duct Diameter
Duct Diameter
When the Tendon Type is Post-Tension, input for the diameter of duct is required. Based on the tendon area, the duct diameter is automatically calculated, which is then referred to for duct diameter input.
 Strand Diameter
Strand Diameter
When the Tendon Type is Pre-Tension, the diameter of strand should be entered. The program automatically calculates the diameter of strand corresponding to the specified Total Tendon Area. The diameter of the strand is used to compute Transfer Length.
 Relaxation Coefficient
Relaxation Coefficient
When Magura is selected
Select 10 or 45 for Relaxation Coefficient (C), which relates to the product. Relaxation coefficients of 10 and 45 may be used for general steel and low-relaxation steel respectively. Losses due to steel relaxation are determined from the following equation:
|
where, |
where, |
: initial stress, |
|
: stress at time t after loading |
|
|
: yield stress (0.1% Offset Yield Stress) |
|||
|
C: Relaxation Coefficient (general steel: 10, low-relaxation steel: 45) |
|||
When European is selected
The following expressions are applied for Class 1 (Ordinary), Class 2 (Low) and Class 3 (Hot rolled) to calculate relaxation loss with time.
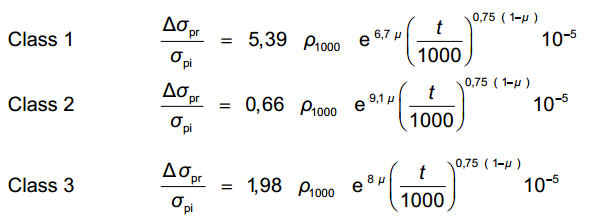
∆σpr: Absolute value of the relaxation losses
σpi: Absolute value of the initial prestress for post-tensioning and maximum tensile stress applied to the tendon minus the immediate losses occurred
t: Time after tensioning (in hours)
µ = σpi /fpk, where fpk is the characteristic value of the tensile strength of the prestressed steel.
ρ1000: Relaxation loss (in %), at 1000 hours after tensioning and at a mean temperature of 20°C
When CEB-FIP(2010) is selected
Enter the loss ratio after 1000 hours steel relaxation by the percentage of initial prestress. Prestress loss due to steel relaxation is determined from the following equation:
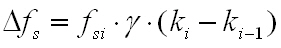
where, |
: initial stress |
|
|
: loss ratio after 1000 hours due to steel relaxation |
|
|
|
: progress of steel relaxation at the last time step |
|
|
||
The progress of steel relaxation with time is as follows:
Time in hour |
1 |
5 |
20 |
100 |
200 |
500 |
1000 |
Slow Development |
20 |
35 |
45 |
65 |
75 |
85 |
100 |
Mean Development |
30 |
45 |
55 |
70 |
80 |
90 |
100 |
Rapid Development |
40 |
55 |
65 |
75 |
85 |
95 |
100 |
Following formula is applied:
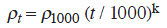
where ρt: the relaxation after t hours, ρ1000: the relaxation after 1000 hours, k =log(ρ1000/ρ100)
When CEB-FIP(1990) is selected
Enter the loss ratio after 1000 hours steel relaxation by the percentage of initial prestress. Prestress loss due to steel relaxation is determined from the following equation:
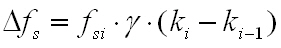
where, |
: initial stress |
|
|
: loss ratio after 1000 hours due to steel relaxation |
|
|
|
: progress of steel relaxation at the last time step |
|
|
||
The progress of steel relaxation with time is as follows:
Time in hour |
1 |
5 |
20 |
100 |
200 |
500 |
1000 |
Relaxation losses at percentage of losses in 1000 hours |
25 |
45 |
55 |
70 |
80 |
90 |
100 |
For an estimation of relaxation up to 30 years, the following formula is applied
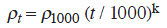
where ρt: the relaxation after t hours, ρ1000: the relaxation after 1000 hours, k to be 0.1549
Note
The relaxation loss after 50 years is taken as three times the 1000 hour loss. The relaxation loss between 30 years and 50 years is linearly interpolated.
When CEB-FIP(1978) is selected
Enter the final loss ratio due to steel relaxation. Prestress loss due to steel relaxation is determined from the following equation:
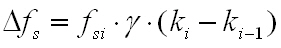
where, |
: initial stress |
|
|
: final loss ratio due to steel relaxation |
|
|
|
: progress of steel relaxation at the last time step |
|
|
||
The progress of steel relaxation with time is as follows:
Progress of relaxation (k) |
Lapse |
k=1/16 ln{ (t-to)/10+1 } |
0 ≤ (t-to) ≤ 1000 |
k={ (t-to)/(0.5x106) }0.2 |
1000 ≤ (t-to) ≤ 0.5x106 |
k=1. 00 |
(t-to) ≥ 0.5 x106 |
where to: the
timing of prestressing
t : the time when tendon loss due to relaxation is evaluated
When AS 5100.5-2017 is selected
The design relaxation of a tendon (R) is determined from the following equation:
k6: a coefficient, dependent on the duration of the prestressing force
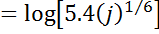
j: time after prestressing, in days
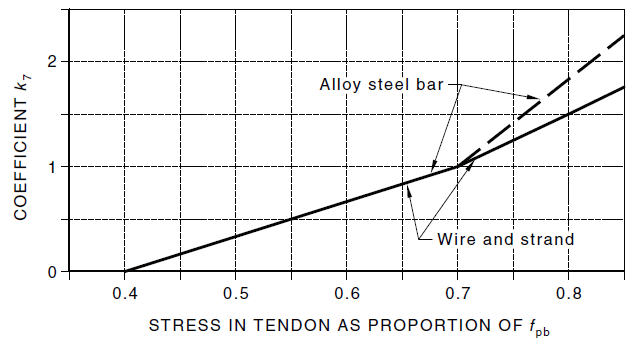
k7: a coefficient, dependent on the stress in the tendon as a proportion of fpb, determined from the figure below.
k8 a coefficient, dependent on the average annual temperature (T) in degrees Celsius, taken as T/20 but not less than 1.0
Rb: basic relaxation of a tendon after one thousand hours at 20°C
The design relaxation of a tendon (R) is determined from the following equation:
When INDIA (IRC:18-2000) is selected
Relaxation loss at 1000 days is as follows (at 20 °C ± 2 °C ):
Initial Stress |
Relaxation loss for Normal relaxation steel (%) |
Relaxation loss for Low relaxation steel (%) |
0.5fp |
0 |
0 |
0.6fp |
2.5 |
1.25 |
0.7fp |
5.0 |
2.5 |
0.8fp |
9.0 |
4.5 |
Relaxation loss, in relation to time, is as follows:
Time (hour) |
1 |
5 |
20 |
100 |
200 |
500 |
1000 |
Relaxation loss (%) |
15 |
25 |
35 |
55 |
65 |
85 |
100 |
When INDIA (IRC:112-2011) is selected
Relaxation loss at 1000 days is as follows (at 20 °C ± 2 °C ):
Initial Stress |
Relaxation loss for Normal relaxation steel (%) |
Relaxation loss for Low relaxation steel (%) |
0.5fp |
0 |
0 |
0.6fp |
2.5 |
1.25 |
0.7fp |
5.0 |
2.5 |
0.8fp |
9.0 |
4.5 |
Relaxation loss, in relation to time, is as follows:
Time (hour) |
1 |
5 |
20 |
100 |
200 |
500 |
1000 |
|
Relaxation loss (%) |
Normal |
34 | 44 | 55 | 70 | 78 | 90 | 100 |
Low |
37 |
47 |
57 |
72 |
79 |
90 |
100 |
|
When JTG04 is selected
if the selects JTG04 standard in the Material Data and selects JTG04 for Relaxation Coefficient in the Tendon Property, the Characteristic Value of Strength (fpk) is automatically entered as per the JTG04 code. If the user does not select JTG04 standard in the Material Data, the user can directly enter the Characteristic Value of Strength (fpk). In case Steelbar540, Steelbar785 or Steelbar930 is selected in the Material Data, the Application of Overstress Reduction Factor is ignored. |
When TB05 is selected
iIf the user selects TB05 standard in the Material Data and selects TB05 for Relaxation Coefficient in the Tendon Property, the Characteristic Value of Strength (fpk) and the Tendon Relaxation Coefficient (ξ) are automatically entered as per the TB05 code. If the user does not select TB05 standard in the Material Data, the user can directly enter the Characteristic Value of Strength (fpk) directly. |
Note
Calculation of Tendon Relaxation Coefficient (ξ) and loss due to Relaxation
When User Defined is selected
Select the user defined relaxation function in hour/day and loss ratio due to steel relaxation relation.
Click [...] button to add/modify User Defined Relaxation Function.
 Curvature Friction Factor
Curvature Friction Factor
To account for friction loss due to the curvature of tendons
 Wobble Friction Factor
Wobble Friction Factor
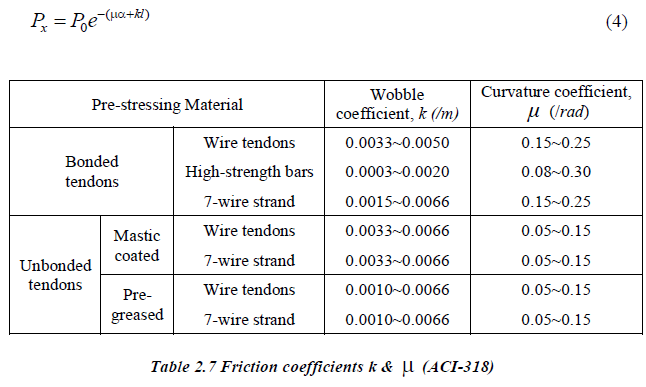
To account for straightness/ length effect (imperfection in alignment along the length of tendon, regardless of straight or draped alignment), if a prestressing force Po is applied at the jacking end, the tendon force Px can be expressed as follows:
Px = Po e-µθ
Where θ is the accumulation of changes in angle along the length being considered.
Θ is composed of two parts-
First is the intentional curvature i.e. due to the intentional curvilinear placement of tendons along the ”Design path”. It is denoted as α.
Second is the unintentional curvature. Since the tendons are secured at selected points only along a design path, in practice the actual path of a flexible tendon will have small deviations from the design path. Also, other construction factors cause added departure of tendon path from its intended profile. The deviations from the design path are referred to as ”wobble” of the tendon. The accumulation of angular change along the tendon length due to its wobble off the intended course is estimated and denoted as γ. Hence the accumulation of angular change becomes (α + γ).
Thus the corrected friction loss relationship becomes:
Px = Po e-µ(α + γ)
Px = Po e-µ{α + (γ/L)L}
(γ/L) is the unintentional angular displacement for internal tendons (per unit length)- specified as k in the Eurocode. Its units are radians/length. Eurocode gives the limit of unintentional angular displacement for internal tendons (per unit length).
The Wobble coefficient is defined as K = µ*γ/L.This is defined in terms of per unit length. For midas Civil we specify the value of wobble coefficient as Wobble Friction Factor. So to incorporate the values of k mentioned in Eurocode, we have to multiply the value with µ and then input in the program.
 Ultimate Strength
Ultimate Strength
 Yield Strength
Yield Strength
 External Cable Moment Magnifier
External Cable Moment Magnifier
Enter the increase of effective prestress of external cable to be used for calculating failure-resisting moment. Entered stress increase will be used for PC design.
 Anchorage Slip (Draw in)
Anchorage Slip (Draw in)
Tendon slippage at the anchor
Begin: slippage at the beginning of tendon if tensioned here
End: slippage at the end of tendon if tensioned here
![]() Bond Type
Bond Type
Bonded: Section properties reflect the duct area after grouting
Unbonded: Section properties exclude the duct area.
![]() To modify the previously entered tendon
data
To modify the previously entered tendon
data
Select the tendon
from the list in the Tendon Property dialog box and click ![]() to change any relevant data.
to change any relevant data.
![]() To delete the previously entered tendon
data
To delete the previously entered tendon
data
Select the tendon
from the list in the Tendon Property dialog box and click ![]() to eliminate any relevant data.
to eliminate any relevant data.
![]() Revision of Civil 2015 (v1.1)
Revision of Civil 2015 (v1.1)
Q1. What are the considerations in the program regarding external tendons?
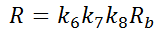
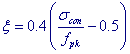
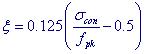 When
When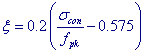 When
When