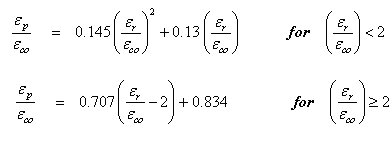Materials
| ||||||||||||||||
|
| ||||||||||||||||
|
| ||||||||||||||||
|
Enter the elastic and plastic material properties. | ||||||||||||||||
|
| ||||||||||||||||
|
| ||||||||||||||||
|
| ||||||||||||||||
|
From the Main Menu select Model > Materials. Click | ||||||||||||||||
|
| ||||||||||||||||
|
| ||||||||||||||||
|
Properties (Material) dialog box
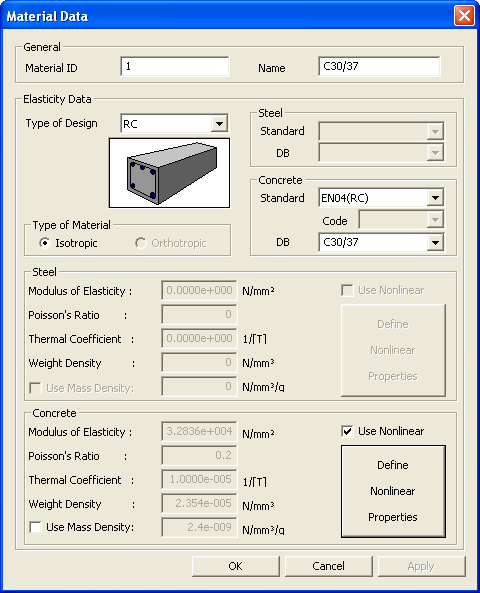
Material Data dialog box
Click
General Material ID: Material property number Name: Material property name
Elasticity Data Type of Design: Select a material property type, and enter the related data. Type of Material Steel Standard: Select the standards of a country in the field. None: The user defines the material properties directly. The user may modify the data obtained from the DB standards. ASTM(S): American Society for Testing Materials CSA(S): Canadian Standards Association BS(S): British Standard BS04(S): British Standards / BS EN 10025 (2004) DIN(S): Deutches Institut fur Normung e.v EN(S): European Standard JIS(S): Japanese Industrial Standards JIS-Civil(S): Japanese Civil Standards GB03(S): Chinese National Standard GB(S): Chinese National Standard JGJ(S): Chinese Industrial Standard JTJ(S): Chinese National Standard of Highway Engineering JTG04(S): Chinese Technical Standard of Highway Engineering. Wire and heat treated rebar materials can be selected from DB TB05(RC): TB 10002.3-2005 (Code for design on reinforced and prestressed concrete structure of railway bridge and culvert) KS(S): Korean Industrial Standard KS-Civil(S): Korean Civil Standards IS(S): Indian Standards CNS(S): Chinese National Standard DB: Select a steel type recognized in each of the standard codes. Steel Nonlinear Properties: Following nonlinear stress-strain curves can be assigned to structural steel.
This is the steel model of Menegotto and Pinto, which was modified by Filippou et al. fy: Yield strength of reinforcing steel E: Modulus of elasticity b: Stiffness reduction factor after yielding Ro, a1, a2: Coefficients for shape index (R) for steel fiber constitutive model This Stress-Strain hysteresis model is outlined as follows: The above formula represents a curved transition from the elastic range to the yielding range. and are normalized values and are calculated as follows: The above formula represents a curved transition from the elastic range to the yielding range.
This
model has two asymptotes as shown below. One asymptote has a slope of
elastic stiffness and the other has a slope of yielding stiffness.
R is the value that can affect the shape of the transition curve and represents the Bauschinger effect. The value of R is determined as follows:
Coefficients
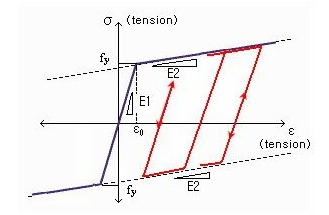
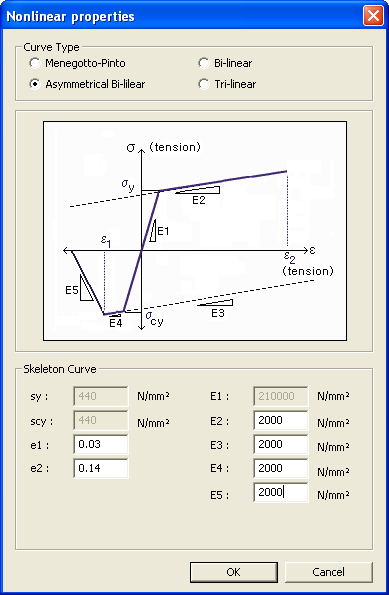
This model represents a general symmetric Bilinear model for reinforcing steel. fy: Yield strength of reinforcing steel E1: Initial stiffness of reinforcing steel E2/E1: Ratio of stiffness after yielding to the initial stiffness As shown in the figure below, the model behaves elastically when it is unloaded and reloaded after yielding. This model has been derived from the general bilinear steel model. Stiffness after compressive and tensile yielding can be freely defined. Buckling and rupturing of reinforcing steel can be considered. σy: Tensile yield strength σcy: Compressive yield strength ε1: Strain at compression buckling of reinforcing steel ε2: Strain at rupturing of reinforcing steel after yielding E1: Initial stiffness of reinforcing steel E2: Stiffness of reinforcing steel after tensile yielding E3: When tension becomes unloaded and reloaded in the compression zone, the E3 line limits the stiffness under compression loading. E4: Stiffness of reinforcing steel after compressive yielding (A negative slope can be specified by entering a negative value.) E5: Stiffness of buckled reinforcing steel after compressive yielding
This Model can describe compressive yielding, tensile yielding, tension rupture, compression buckling, etc of reinforcing steel. The figure below shows the possible hysteresis states. Each state is explained as follows: Since tension behavior is the major cause of hysteresis in steel, the loading direction basically follows tension. During unloading, the loading direction changes from tension to compression, and vice-versa during reloading. State 1: It represents the elastic behavior, and the slope is E1. 1 → 2 = Transition to yielding state. The slope is E2 under tensile yielding and E4 under compressive yielding. State 2: It represents the state after the yielding starts, and the slope is E2. 2 → 4 = Unload and reload after yielding. 2 → 8 = Tension is sustained after yielding, and thereafter, tension rupture is caused. The stress is always '0' after the rupture. State 3: Unload continuously and as a result the compression zone yields. The slope is E2. E3 should be input such that the point intersecting the line E3 and strain axis is greater than . 3 → 4 = Reload. The slope is E1. 3 → 5 = As unloading continues, the compression strain exceeds and compression buckling starts. The slope is E5. State 4: Unloading and reloading with slope E1 (elastic stiffness) 4 → 2 = As reloading continues, the state changes to tensile yielding state. Or as unloading continues, the state changes to compressive yielding state. 4 → 3 = As unloading continues, compressive yielding occurs. It can be assumed that compressive yielding occurs at the intersection with line E3. 4 → 5 = As unloading continues, compression buckling starts. State 5: When compression strain exceeds buckling strain, buckling of reinforcing steel takes place. The slope is E5. 5 → 4 = Reloading continues during compression buckling. 5 → 7 = As compression is sustained, the reinforcing steel undergoes complete compression buckling. The stress becomes '0' at compression during and after State 7. State 6: Reload after compression buckling. Reloading will progress towards before tensile yielding occurs. Reloading will progress towards the maximum point in the tension zone after tensile yielding occurs. 6 → 2 = As reloading continues, tensile yielding takes place. 6 →-1 = Unload while reloading. State 7: Once complete compression buckling occurs, further compressive stresses cannot be generated. Although compressive stress becomes '0' it can still resist tension. 7 → 6 = Reloading occurs and progresses towards the maximum tension point. State 8: Once tension rupture occurs, further tensile stresses cannot be generated, and neither will compressive stresses be generated. State 9: Unload while reloading after compression buckling (State 6). The slope is E1 (elastic stiffness). -1 → 6 = Reloading progresses towards the maximum tension point. -1 → 7 = Unloading and the subsequent transition to complete compression buckling As stated above, this model considers the various states and transitions. If the user is familiar with this model and applies the experimental parameters properly, it can be a very efficient tool. However, the user must use caution when using this model for limit states, such as tension rupture and compression buckling, as the resistance becomes '0'. This model represents a Trilinear model of three slopes. The hysteresis can be defined by the stress-strain relationship and the stress-stiffness reduction ratio relationship. When unloading and reloading, the model behaves elastically.
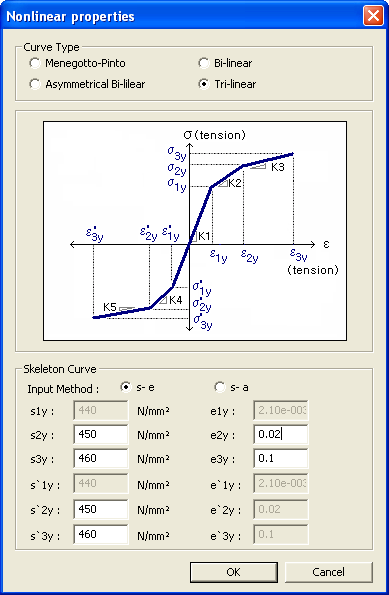
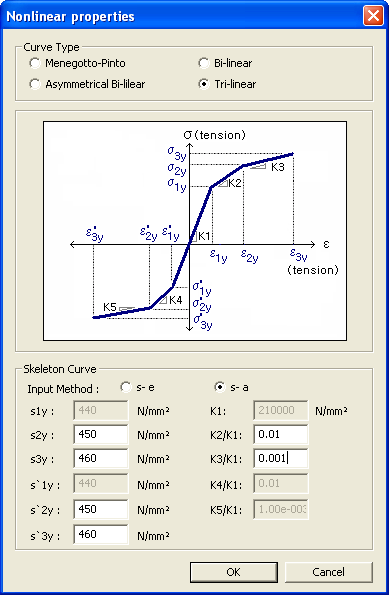
Stress-Strain Definition
Stress-Stiffness reduction ratio Definition
σ1y: First yield strength in tension σ2y: Second yield strength in tension σ3y: Stiffness after second tensile yielding (required for K3 calculation) σ'1y: First yield strength in compression σ'2y: Second yield strength in compression σ'3y: Stiffness after second compressive yielding (required for K5 calculation) ε1y: Strain at first yielding in tension ε2y: Strain at second yielding in tension ε3y: Strain after second tensile yielding (required for K3 calculation) ε'1y: Strain at first yielding in compression ε'2y: Strain at second yielding in compression ε'3y: Strain after second compressive yielding (required for K5 calculation) K: Initial stiffness of reinforcing steel K2/K1: Ratio of stiffness after first tensile yielding to the initial stiffness K3/K1: Ratio of stiffness after second tensile yielding to the initial stiffness K4/K1: Ratio of stiffness after first compressive yielding to the initial stiffness K5/K1: Ratio of stiffness after second compressive yielding to the initial stiffness Note When ε1y~ε'3y are entered in the 'σ - ε' input method, and the 'σ - α' input method is selected, K1, K2/K1, K3/K1, etc. are automatically calculated. Also the reverse calculation is automatically done. Concrete Standard: Select the standards of a country in the field. None: The user defines the material properties directly. The user may modify the data obtained from the DB standards. ASTM(RC): American Society for Testing Materials CSA(RC): Canadian Standards Association BS(RC): British Standard Note EN(RC): European Code JIS(RC): Japanese Industrial Standards GB(RC): Chinese National Standard GB-Civil(RC): Chinese National Standard JTG04(RC): Chinese Technical Standard of Highway Engineering TB05(RC): TB 10002.3-2005 (Code for design on reinforced and prestressed concrete structure of railway bridge and culvert) KS01(RC): Korea Industrial Standards (in SI unit system) KS(RC): Korean Industrial Standards (in MKS unit system) KS-Civil(RC): Korean Civil Standards IS(RC): Indian Standards CNS(RC): Chinese National Standard JTG04(S) : Jiao Tongbu Gong Lu Biao Zhun (China) UNI(RC): Italian National Standards DB: Select a concrete type recognized in each of the standard codes. Concrete Nonlinear Properties: Following nonlinear stress-strain curves can be assigned to structural steel. This stress-strain curve is as per the clause 3.1.5(1) of EN1992-1-1:2004.
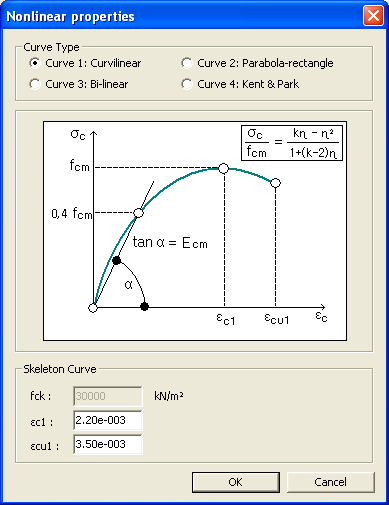
The relation between σc and εc (compressive stress and shortening strain shown as absolute values) for short term uniaxial loading is described by the expression: The default values of
This stress-strain curve is as per the clause 3.1.7(1) of EN1992-1-1:2004.
The
default values of This stress-strain curve is as per the clause 3.1.7(2) of EN1992-1-1:2004.
The
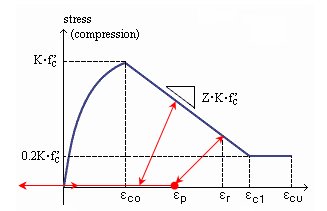
default values of This Kent and Park (1973) concrete model, which was modified by Scott, et al. (1982), can consider the Confinement Effect due to reinforcing and is rated highly because of its clear formation and accurate analysis.
Kent & Park Model
Note
In this model, the concrete tensile strength is ignored since it has little effect on the entire member. Hysteresis characteristics of this model are as follows: a.
When a member is unloaded under compression, its behavior is represented
by the line connecting
b. Tensile strength is ignored in this model. Therefore, under Complete Unloading or Open Crack, the stress becomes '0'(as shown in the above figure). c.
When reloaded, the stress values before attaining Note Material properties of reinforcing steel can be defined in Rebar Material Properties. | ||||||||||||||||
|
|
.jpg)
 For new or additional material properties
For new or additional material properties in the Properties dialog box and enter the
following data:
in the Properties dialog box and enter the
following data: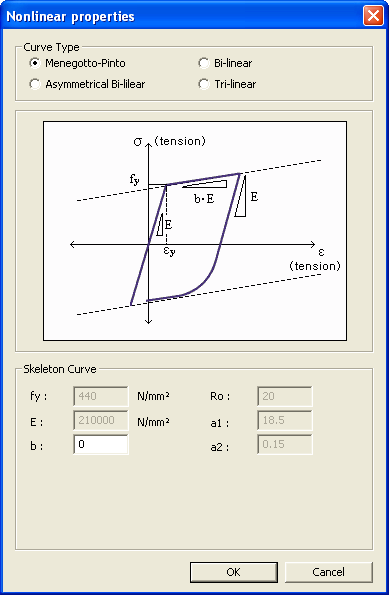
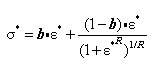
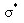 and
and 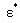 are normalized values and are calculated as follows:
are normalized values and are calculated as follows: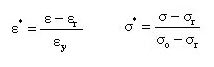
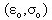 is
a point intersected by two asymptotes.
is
a point intersected by two asymptotes.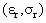 is the point where the
last unloading occurred. While unloading and reloading, these points are
updated, so that the transition curve is affected.
is the point where the
last unloading occurred. While unloading and reloading, these points are
updated, so that the transition curve is affected. 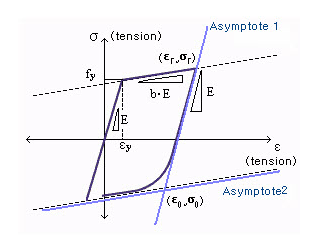
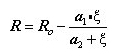
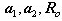 are determined from
experimental hysteresis results. MIDAS uses 18.5, 0.15 and 20, respectively,
as default values. These default values are suggested in the original
reference (Menegotto and Pinto,1973).
are determined from
experimental hysteresis results. MIDAS uses 18.5, 0.15 and 20, respectively,
as default values. These default values are suggested in the original
reference (Menegotto and Pinto,1973). 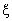 is a shape coefficient and updated at
every unloading.
is a shape coefficient and updated at
every unloading.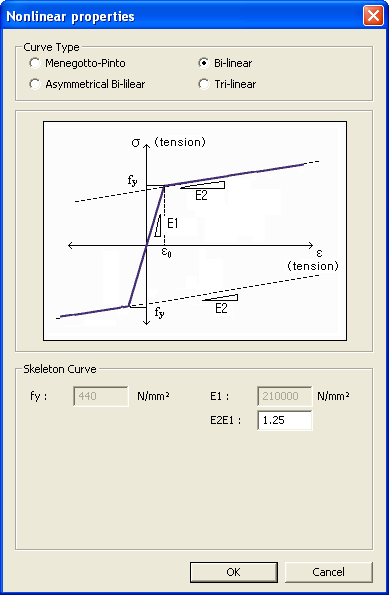
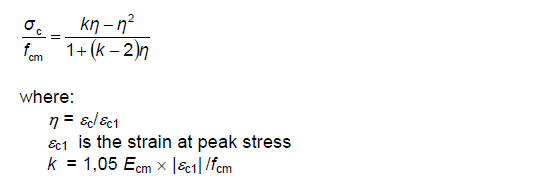
 and
and  are taken from Table
3.1 of EN1992-1-12004.
are taken from Table
3.1 of EN1992-1-12004.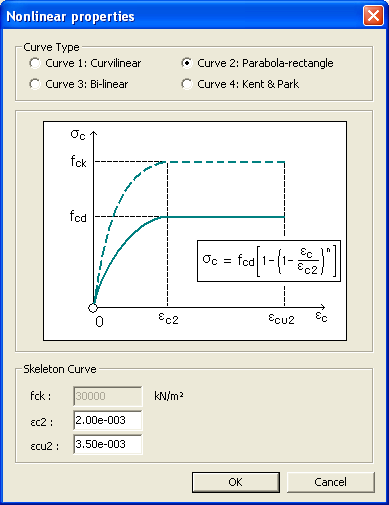
 and
and  are taken
from Table 3.1 of EN1992-1-1:2004.
are taken
from Table 3.1 of EN1992-1-1:2004.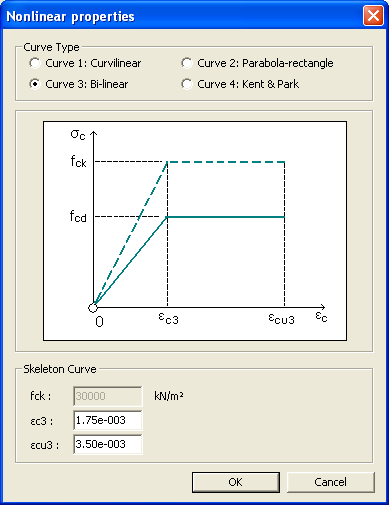
 and
and 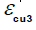 are taken
from Table 3.1 of EN1992-1-1:2004.
are taken
from Table 3.1 of EN1992-1-1:2004.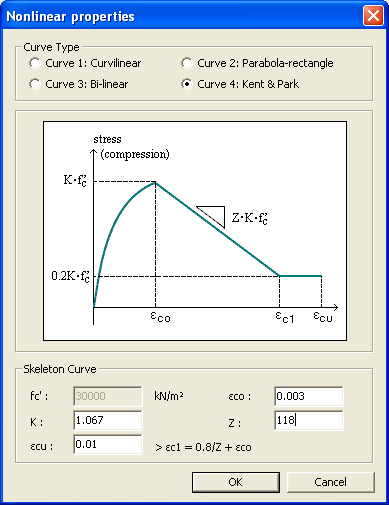
.bmp)
 : Ratio of the
volume of hoop reinforcement to the volume of concrete core measured to
outside of stirrups
: Ratio of the
volume of hoop reinforcement to the volume of concrete core measured to
outside of stirrups  : Yield strength
of stirrup steel
: Yield strength
of stirrup steel
.bmp)
.bmp)
 : Width of concrete
core measured to outside of stirrups Sh
: Width of concrete
core measured to outside of stirrups Sh 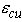 can be obtained by
the proposed equation of Scott et al, or another value may be used at
user's discretion.
can be obtained by
the proposed equation of Scott et al, or another value may be used at
user's discretion.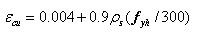
 and
and 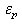 ; where
; where