Materials
Enter the linear and nonlinear material properties.
From the Main Menu select Model > Materials.
Click ![]() Material
in the Icon
Menu.
Material
in the Icon
Menu.
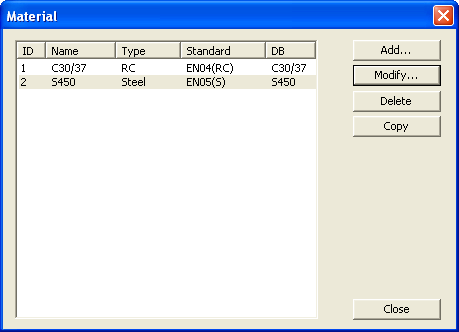
Properties (Material) dialog box
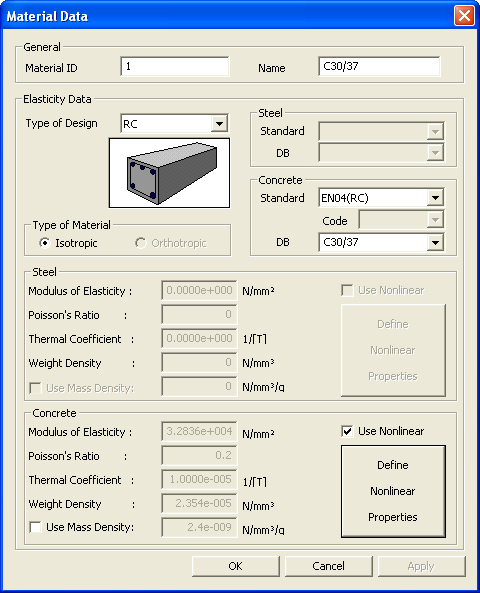
Material Data dialog box
![]() For new or additional material properties
For new or additional material properties
Click ![]() in the Properties
dialog box and enter the following data:
in the Properties
dialog box and enter the following data:
General
Material ID: Material property number
Name: Material property name
Elasticity Data
Type of Design: Select a material property type, and enter the related data.
Type of Material
Steel
Standard: Select the standards of a country in the field.
None: The user defines the material properties directly. The user may modify the data obtained from the DB standards.
ASTM(S): American Society for Testing Materials
CSA(S): Canadian Standards Association
BS(S): British Standard
BS04(S): British Standards / BS EN 10025 (2004)
DIN(S): Deutches Institut fur Normung e.v
EN(S) / EN05(S) / EN05-PS(S) / EN05-SW(S): European Standard
UNI(S): Italian national standard
IS(S): Indian Standards
GOST(S): Russian national standard
JIS(S): Japanese Industrial Standards
JIS-Civil(S): Japanese Civil Standards
GB(S) / GB03(S): Chinese National Standard
JGJ(S): Chinese Industrial Standard
JTJ(S): Chinese National Standard of Highway Engineering
JTG04(S): Chinese Technical Standard of Highway Engineering. Wire and heat treated rebar materials can be selected from DB
TB05(RC): TB 10002.3-2005 (Code for design on reinforced and prestressed concrete structure of railway bridge and culvert)
KS(S): Korean Industrial Standard
KS-Civil(S): Korean Civil Standard
CNS(S): Taiwanese national standard
DB: Select a steel type recognized in each of the standard codes.
Steel Nonlinear Properties: Following nonlinear stress-strain curves can be assigned to structural steel.
This is the steel model of Menegotto and Pinto, which was modified by Filippou et al.
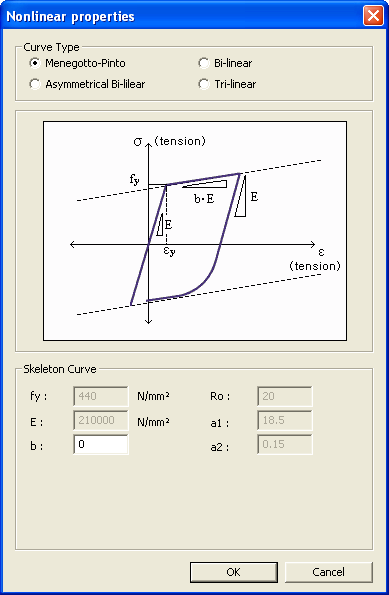
fy: Yield strength of reinforcing steel
E: Modulus of elasticity
b: Stiffness reduction factor after yielding
Ro, a1, a2: Coefficients for shape index (R) for steel fiber constitutive model
This Stress-Strain hysteresis model is outlined as follows:
The above formula represents a curved transition from the elastic range to the yielding range.
and are normalized values and are calculated as follows:
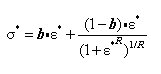
The above formula represents a curved transition from the elastic range to the yielding range.
![]() and
and ![]() are normalized values
and are calculated as follows:
are normalized values
and are calculated as follows:
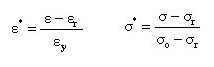
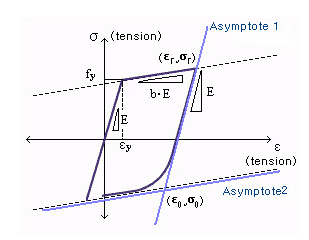
This
model has two asymptotes as shown below. One asymptote has
a slope of elastic stiffness and the other has a slope of
yielding stiffness.![]() is
a point intersected by two asymptotes.
is
a point intersected by two asymptotes.![]() is the point where the last unloading occurred.
While unloading and reloading, these points are updated, so
that the transition curve is affected.
is the point where the last unloading occurred.
While unloading and reloading, these points are updated, so
that the transition curve is affected.
R is the value that can affect the shape of the transition curve and represents the Bauschinger effect. The value of R is determined as follows:
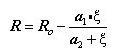
Coefficients ![]() are determined from experimental
hysteresis results. MIDAS uses 18.5, 0.15 and 20, respectively,
as default values. These default values are suggested in the
original reference (Menegotto and Pinto,1973).
are determined from experimental
hysteresis results. MIDAS uses 18.5, 0.15 and 20, respectively,
as default values. These default values are suggested in the
original reference (Menegotto and Pinto,1973).
![]() is
a shape coefficient and updated at every unloading.
is
a shape coefficient and updated at every unloading.
This model represents a general symmetric Bilinear model for reinforcing steel.
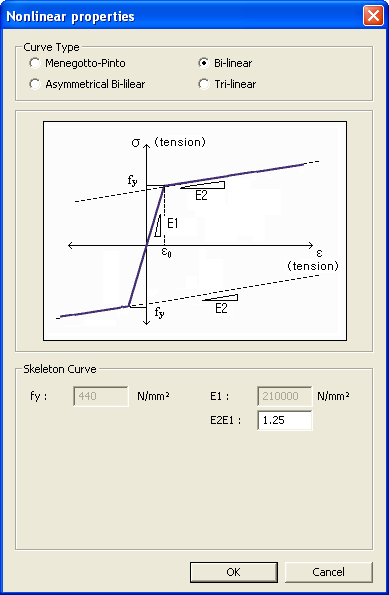
fy: Yield strength of reinforcing steel
E1: Initial stiffness of reinforcing steel
E2/E1: Ratio of stiffness after yielding to the initial stiffness
As shown in the figure below, the model behaves elastically when it is unloaded and reloaded after yielding.
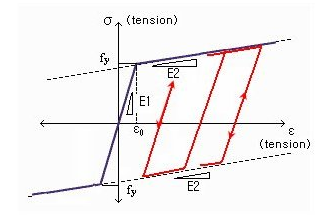
This model has been derived from the general bilinear steel model. Stiffness after compressive and tensile yielding can be freely defined. Buckling and rupturing of reinforcing steel can be considered.
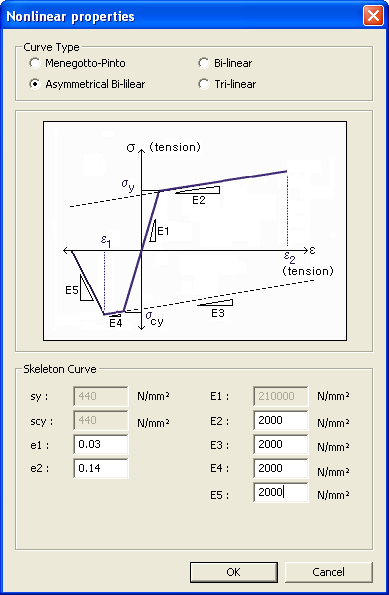
σy: Tensile yield strength
σcy: Compressive yield strength
ε1: Strain at compression buckling of reinforcing steel
ε2: Strain at rupturing of reinforcing steel after yielding
E1: Initial stiffness of reinforcing steel
E2: Stiffness of reinforcing steel after tensile yielding
E3: When tension becomes unloaded and reloaded in the compression zone, the E3 line limits the stiffness under compression loading.
E4: Stiffness of reinforcing steel after compressive yielding
(A negative slope can be specified by entering a negative value.)
E5: Stiffness of buckled reinforcing steel after compressive yielding

This Model can describe compressive yielding, tensile yielding, tension rupture, compression buckling, etc of reinforcing steel. The figure below shows the possible hysteresis states.
Each state is explained as follows:
Since tension behavior is the major cause of hysteresis in steel, the loading direction basically follows tension. During unloading, the loading direction changes from tension to compression, and vice-versa during reloading.
State 1: It represents the elastic behavior, and the slope is E1.
1 → 2 = Transition to yielding state. The slope is E2 under tensile yielding and E4 under compressive yielding.
State 2: It represents the state after the yielding starts, and the slope is E2.
2 → 4 = Unload and reload after yielding.
2 → 8 = Tension is sustained after yielding, and thereafter, tension rupture is caused. The stress is always '0' after the rupture.
State 3: Unload continuously and as a result the compression zone yields. The slope is E2. E3 should be input such that the point intersecting the line E3 and strain axis is greater than .
3 → 4 = Reload. The slope is E1.
3 → 5 = As unloading continues, the compression strain exceeds and compression buckling starts. The slope is E5.
State 4: Unloading and reloading with slope E1 (elastic stiffness)
4 → 2 = As reloading continues, the state changes to tensile yielding state. Or as unloading continues, the state changes to compressive yielding state.
4 → 3 = As unloading continues, compressive yielding occurs. It can be assumed that compressive yielding occurs at the intersection with line E3.
4 → 5 = As unloading continues, compression buckling starts.
State 5: When compression strain exceeds buckling strain, buckling of reinforcing steel takes place. The slope is E5.
5 → 4 = Reloading continues during compression buckling.
5 → 7 = As compression is sustained, the reinforcing steel undergoes complete compression buckling. The stress becomes '0' at compression during and after State 7.
State 6: Reload after compression buckling. Reloading will progress towards before tensile yielding occurs. Reloading will progress towards the maximum point in the tension zone after tensile yielding occurs.
6 → 2 = As reloading continues, tensile yielding takes place.
6 →-1 = Unload while reloading.
State 7: Once complete compression buckling occurs, further compressive stresses cannot be generated. Although compressive stress becomes '0' it can still resist tension.
7 → 6 = Reloading occurs and progresses towards the maximum tension point.
State 8: Once tension rupture occurs, further tensile stresses cannot be generated, and neither will compressive stresses be generated.
State 9: Unload while reloading after compression buckling (State 6). The slope is E1 (elastic stiffness).
-1 → 6 = Reloading progresses towards the maximum tension point.
-1 → 7 = Unloading and the subsequent transition to complete compression buckling
As stated above, this model considers the various states and transitions. If the user is familiar with this model and applies the experimental parameters properly, it can be a very efficient tool. However, the user must use caution when using this model for limit states, such as tension rupture and compression buckling, as the resistance becomes '0'.
This model represents a Trilinear model of three slopes. The hysteresis can be defined by the stress-strain relationship and the stress-stiffness reduction ratio relationship.
When unloading and reloading, the model behaves elastically.
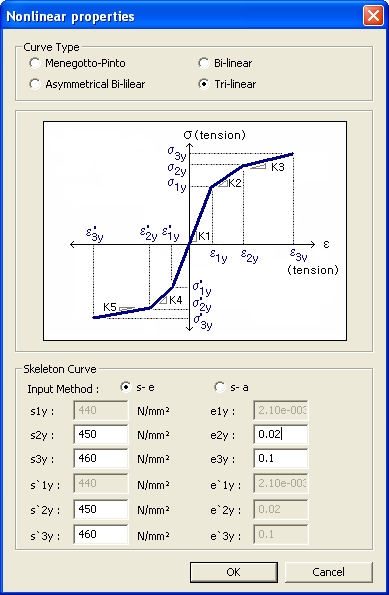
Stress-Strain Definition
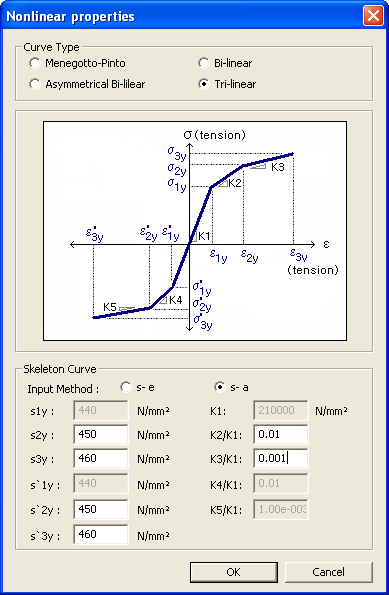
Stress-Stiffness reduction ratio Definition
σ1y: First yield strength in tension
σ2y: Second yield strength in tension
σ3y: Stiffness after second tensile yielding (required for K3 calculation)
σ'1y: First yield strength in compression
σ'2y: Second yield strength in compression
σ'3y: Stiffness after second compressive yielding (required for K5 calculation)
ε1y: Strain at first yielding in tension
ε2y: Strain at second yielding in tension
ε3y: Strain after second tensile yielding (required for K3 calculation)
ε'1y: Strain at first yielding in compression
ε'2y: Strain at second yielding in compression
ε'3y: Strain after second compressive yielding (required for K5 calculation)
K: Initial stiffness of reinforcing steel
K2/K1: Ratio of stiffness after first tensile yielding to the initial stiffness
K3/K1: Ratio of stiffness after second tensile yielding to the initial stiffness
K4/K1: Ratio of stiffness after first compressive yielding to the initial stiffness
K5/K1: Ratio of stiffness after second compressive yielding to the initial stiffness
Note
When ε1y~ε'3y are entered in the 'σ - ε' input method, and the 'σ - α' input method is selected, K1, K2/K1, K3/K1, etc. are automatically calculated. Also the reverse calculation is automatically done.
Concrete
Standard: Select the standards of a country in the field.
None: The user defines the material properties directly. The user may modify the data obtained from the DB standards.
ASTM(RC): American Society for Testing Materials
CSA(RC): Canadian Standards Association
BS(RC): British Standard
Note
When material data are defined per BS or Chinese Standards,
Cubic compressive strength is used as opposed to Cylinder
strength.
EN(RC) / EN04(RC): Eurocode
UNI(RC) / NTC08(RC) / NTC12(RC): Italian National Standards
IS(RC): Indian Standards
GOST-SP(RC) / GOST-SNiP(RC): Russian national standard
JIS(RC): Japanese Industrial Standard
GB(RC): Chinese National Standard
GB-Civil(RC): Chinese National Standard
JTG04(RC): Chinese Technical Standard of Highway Engineering
TB05(RC): TB 10002.3-2005 (Code for design on reinforced and prestressed concrete structure of railway bridge and culvert)
KS01(RC): Korea Industrial Standards (in SI unit system)
KS(RC): Korean Industrial Standards (in MKS unit system)
KS-Civil(RC): Korean Civil Standards
CNS(RC) / CNS560(RC): Taiwanese National Standard
JTG04(S) : Jiao Tongbu Gong Lu Biao Zhun (China)
DB: Select a concrete type recognized in each of the standard codes.
Concrete Nonlinear Properties: Following nonlinear stress-strain curves can be assigned to structural steel.
This stress-strain curve is as per the clause 3.1.5(1) of EN1992-1-1:2004.
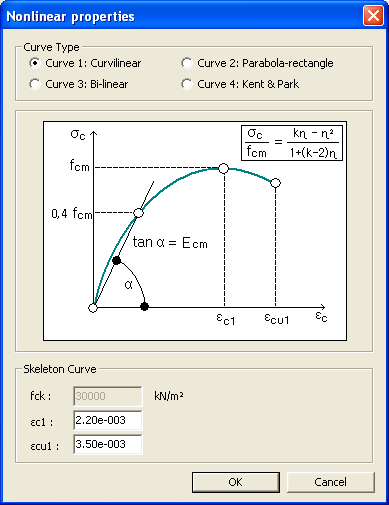
The relation between σc and εc (compressive stress and shortening strain shown as absolute values) for short term uniaxial loading is described by the expression:
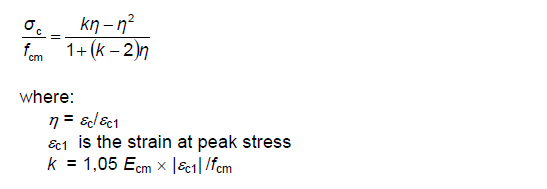
The default
values of ![]() and
and ![]() are taken from Table 3.1 of EN1992-1-12004.
are taken from Table 3.1 of EN1992-1-12004.
This stress-strain curve is as per the clause 3.1.7(1) of EN1992-1-1:2004.
The
default values of ![]() and
and ![]() are taken
from Table 3.1 of EN1992-1-1:2004.
are taken
from Table 3.1 of EN1992-1-1:2004.
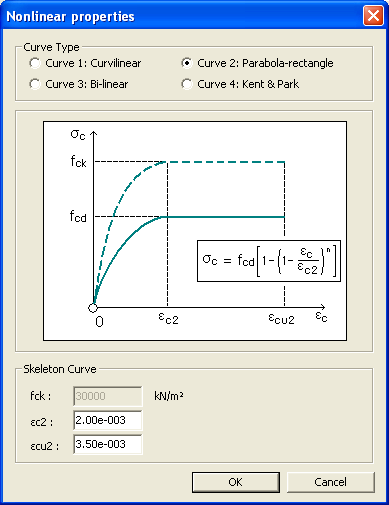
This stress-strain curve is as per the clause 3.1.7(2) of EN1992-1-1:2004.
The
default values of ![]() and
and ![]() are taken from Table 3.1 of EN1992-1-1:2004.
are taken from Table 3.1 of EN1992-1-1:2004.
This Kent and Park (1973) concrete model, which was modified by Scott, et al. (1982), can consider the Confinement Effect due to reinforcing and is rated highly because of its clear formation and accurate analysis.
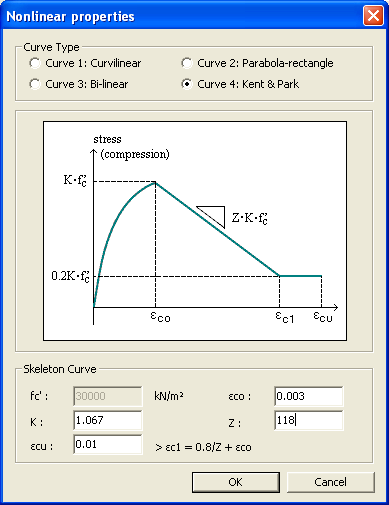
Kent & Park Model
|
Concrete compressive cylinder strength |
|
Factor, which accounts for the strength increase due to confinement |
|
|
|
Strain at compressive Crushing |
|
Strain at maximum compressive strength |
|
|
|
Strain softening slope - coefficient representing the stiffness in the concrete softening zone after compression yielding |
|
Sh: Center to center spacing of stirrups or hoop sets |
Note
![]() can be obtained by the proposed equation of Scott et al, or
another value may be used at user's discretion.
can be obtained by the proposed equation of Scott et al, or
another value may be used at user's discretion.
![]()
In this model, the concrete tensile strength is ignored since it has little effect on the entire member.
Hysteresis characteristics of this model are as follows:
a.
When a member is unloaded under compression, its behavior
is represented by the line connecting ![]() and
and ![]() ; where
; where ![]() is the strain at
the beginning of unloading and
is the strain at
the beginning of unloading and ![]() is
a certain point on the strain axis. As the compression increases,
the slope of this line becomes flatter. The relationship is
defined as:
is
a certain point on the strain axis. As the compression increases,
the slope of this line becomes flatter. The relationship is
defined as:
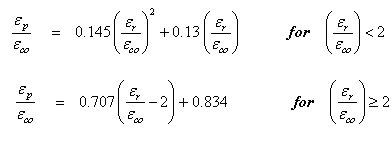
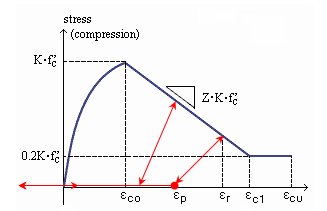
b. Tensile strength is ignored in this model. Therefore, under Complete Unloading or Open Crack, the stress becomes '0'(as shown in the above figure).
c.
When reloaded, the stress values before attaining ![]() shall be taken as '0'.
Once the compressive strain exceeds
shall be taken as '0'.
Once the compressive strain exceeds![]() , reloading
is applied along the line where the unloading occurred. In
reality, Unloading and Reloading cannot be applied linearly,
since it is actually a nonlinear application. However since
there is not much difference between linear and nonlinear
behavior, the results will be accurate enough even if linear
Unloading and Reloading is assume.
, reloading
is applied along the line where the unloading occurred. In
reality, Unloading and Reloading cannot be applied linearly,
since it is actually a nonlinear application. However since
there is not much difference between linear and nonlinear
behavior, the results will be accurate enough even if linear
Unloading and Reloading is assume.
This is the concrete model confined by transverse rebar, which was suggested by Mander (1988). Transverse rebars are provided to confine core concrete, and to prevent buckling failure of main rebars and shear failure of the member. Compressive concrete confined by transverse rebar can increase strength and ductility of a member due to the confinement effect.
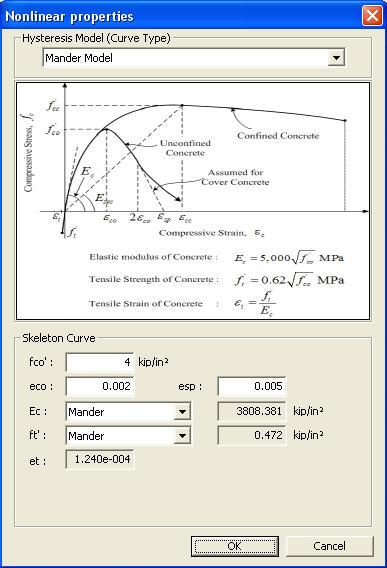
Mander unconfined concrete model
f'co |
Unconfined concrete compressive strength |
eco |
Unconfined concrete strain at f'co |
esp |
Spalling strain |
Ec |
Elastic modulus of concrete. When "Mander" is selected, it is automatically calculated. When "User Input" is selected, the user can directly enter the value. |
f't |
Tensile strength of concrete. When "Neglect Tensile Strength" is selected, tensile strength of concrete is ignored. When "Mander." is selected, it is automatically calculated. When "User Input" is selected, the user can directly enter the value. |
et |
Tensile strain of concrete at f't. It is automatically calculated based on the tensile strength. |
Note
1. Confined concrete properties and confined area can be defined after Mander unconfined concrete properties and section shape are defined. The Confined Area and Confined Concrete Properties menus will be shown under the concrete material from Works Tree as shown below.
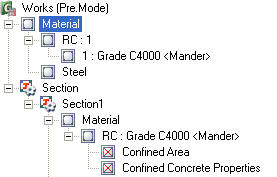
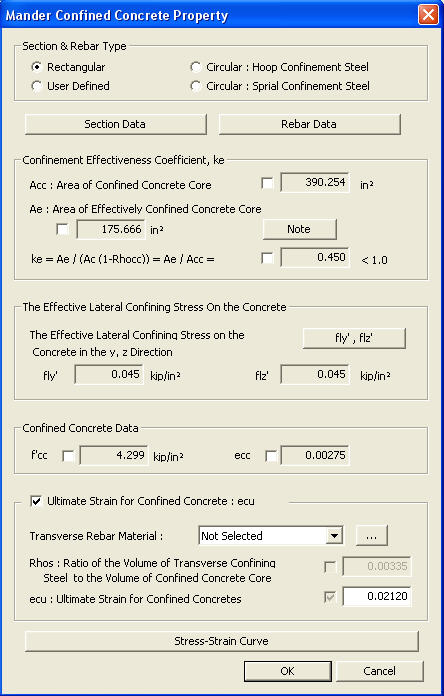
2. Mander Confined Concrete Property
Section & Rebar Type: Rectangular
Section Data
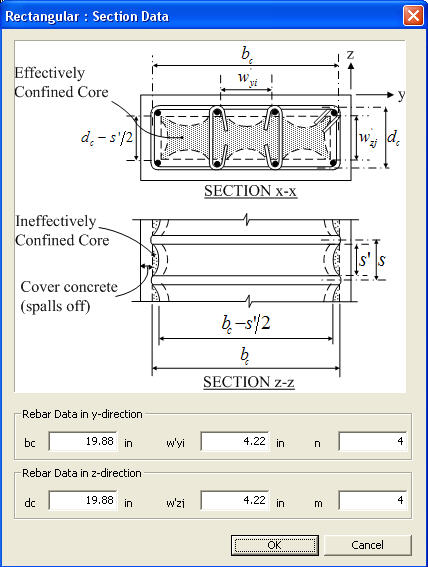
bc and dc: Core dimensions to centerlines of perimeter hoop in y and z directions, respectively
w'yi and w'zi: Clear distances between adjacent longitudinal bars in y and z directions, respectively
n and m: Number of spacings between longitudinal bars in y and z directions, respectively
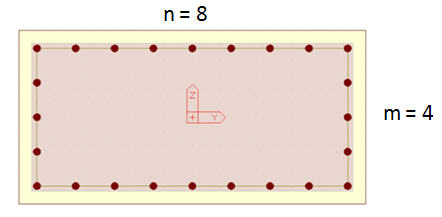
Rebar Data
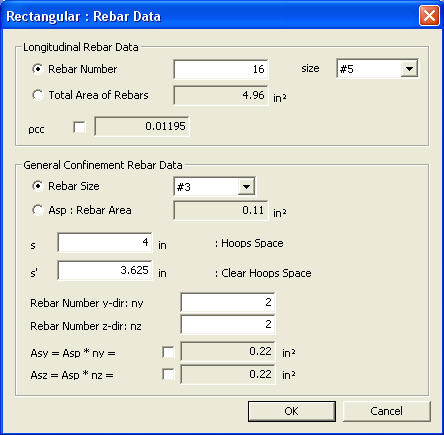
General Confinement Rebar Data
Asp: Rebar area of one leg of confinement rebar
Rebar Number y-dir and Rebar Number z-dir: Total number of legs of confinement rebar in y and z directions, respectively
Section & Rebar Type: Circular
Section Data
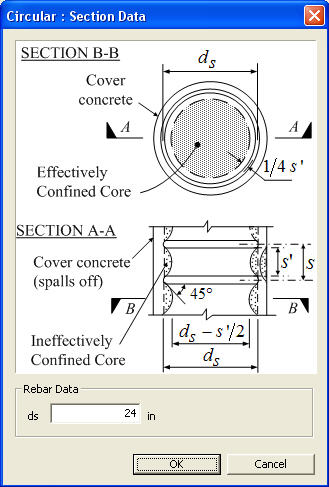
ds: Diameter of spiral or circular hoop between bar centers
Rebar Data
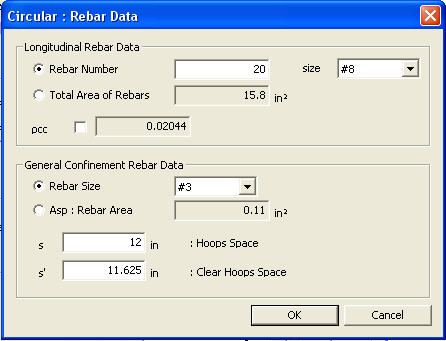
General Confinement Rebar Data
Asp: Rebar area of one leg of confinement rebar
Ultimate Strain for Confined Concrete: ecu
Ultimate concrete compression strain for confined concrete is calculated using the method proposed by Mander et al. (1984), which predicts the longitudinal concrete compressive strain at first hoop fracture based on energy balance approach.
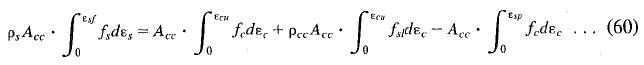
In this equation, the assumption is made as follows according to Mander et al. (1984).
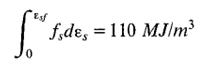
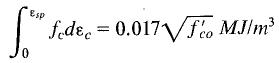
![]() Revision
of GSD v230
Revision
of GSD v230
This stress-strain curve is as per the SP 63.13330.
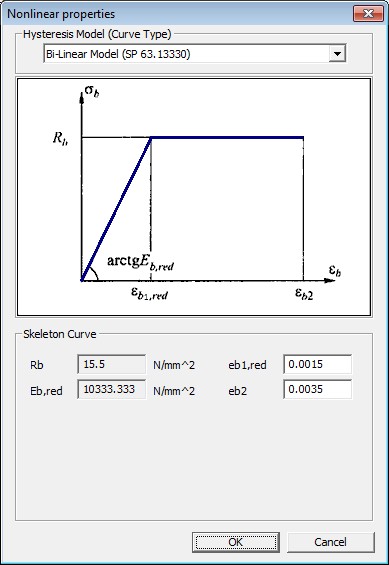
Bilinear Model
The reduced modulus of elasticity is determined as follows:
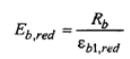
where Rb is design strength of concrete.
εb1,red is the strain corresponding to the point from which yielding begins.
εb2 is the ultimate strain at which the ultimate resistance of section is determined.
This stress-strain curve is as per the SP 63.13330.
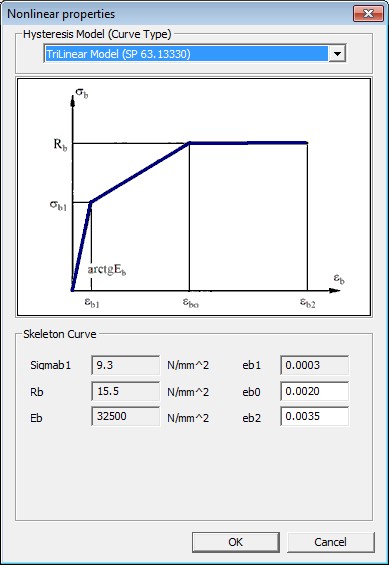
Trilinear Model
The stress-strain relationship is determined as follows:
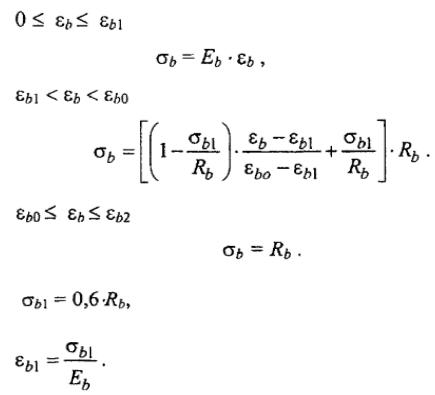
where Rb is design strength of concrete.
Eb is the initial modulus of elasticity of concrete.
εb1 is the strain corresponding to the point from which the first yielding begins.
εb0 is the strain corresponding to the point from which the second yielding begins.
εb2 is the ultimate strain at which the ultimate resistance of section is determined.
Note
Material properties of reinforcing steel can be defined in Rebar Material Properties.
.bmp)
.bmp)