 Revision of Ver.7.4.1
Revision of Ver.7.4.1 Revision of Ver.7.4.1
Revision of Ver.7.4.1
Function
Enter section properties for line elements (Truss, Tension-only, Compression-only, Cable, Gap, Hook, Beam Element).
Call
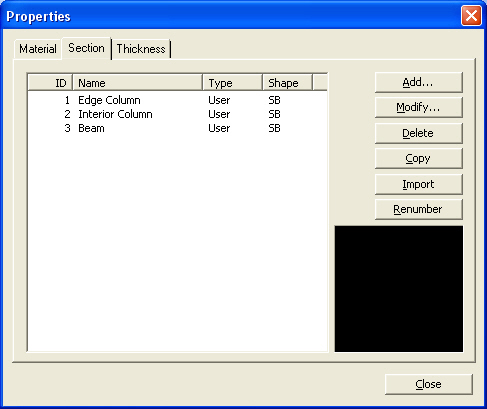
From the Main Menu select Model > Properties > Section.
Select Geometry > Properties > Section in the Menu tab of the Tree Menu.
Click .jpg) Section in the Property Tool Bar.
Section in the Property Tool Bar.
Enter
To enter new or additional section properties
Click  in the
Properties dialog box and enter the following: Enter the section properties
by entry types.
in the
Properties dialog box and enter the following: Enter the section properties
by entry types.
Modification of previously entered section data
Select the section to be modified
from the list in the Section dialog box and click  to modify
the related data.
to modify
the related data.
Removal of previously entered section data
Select the section to be deleted
from the list in the Section dialog box and click  .
.
To copy previously entered section data
Select the section to be copied
from the list in the Section dialog box and click  .
.
To modify section data from an existing fn.MCB file
Click  and select
the MCB file containing the section data or specify a file name then click
and select
the MCB file containing the section data or specify a file name then click
 . [Details]
. [Details]
Section List
Display section data contained in the existing fn.MCB file.
Selected
List
Select section data to be imported and register them in the Selected List.
Note
If a fn.MCB is selected, all the section data contained
in the existing fn.MCB file are registered in the Selected List.
Numbering
Type
Specify the Import mode for section numbers.
Keep
ID
Import the data keeping the same section numbers.
New
ID
Assign new numbers to the imported section data.
To modify previously entered section property numbers
Select the section property
numbers to be renumbered from the list in the Properties dialog box and
modify the related data followed by clicking  . [Details]
. [Details]

Renumbering Section Number dialog box
Start
number
Assign a new starting number for the material to be modified.
Increment
Enter the increment for numbering material property numbers.
Change
element's material number
Modify a material property number. Using this option will modify the previously
defined material property number. If this option is not checked, the selected
material having previously defined number will become undefined and the
additional user-defined material number will be created without any assigned
elements.
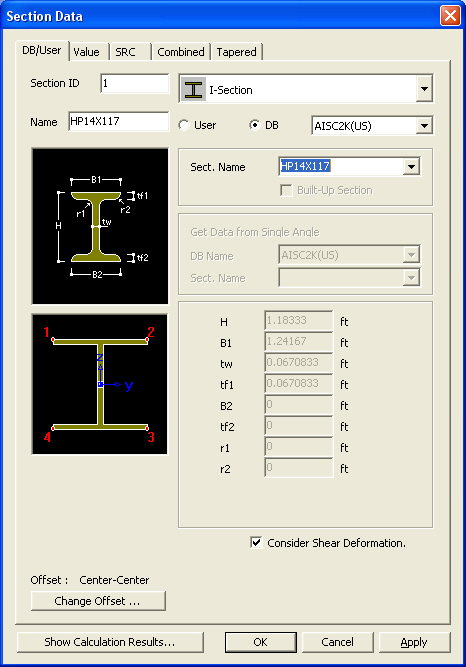
Section Data Dialog
 Section ID
Section ID
Section number (Auto-set to the last section number +1)
Note
Up to 999999 Section ID's can be assigned.
 Name
Name
Section name (Sect. Name by default if not specified)
 Offset
Offset
Display the section Offset currently set.
Location of the Centroid of a section is set as default. Click  to
specify a section Offset away from the Centroid. Use
to
specify a section Offset away from the Centroid. Use .jpg) Hidden
to verify the input. [Details]
Hidden
to verify the input. [Details]
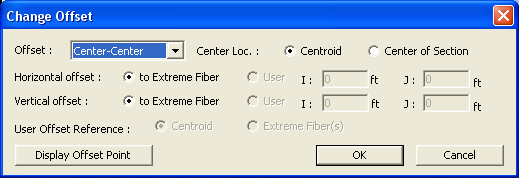
Change Offset dialog box
Offset: Specify the section Offset from the location options shown in the figure below.
Horizontal Offset: Specify the Offset in the transverse direction. "to Extreme Fiber" assigns the offset to the outer-most point. For a specific location of Offset, select 'User"and enter the distance from the "Centroid" to the desired Offset location. Unless the Offset is "Center-Center" the Horizontal Offset can be entered as the "User" type. For a tapered (non-prismatic) section, data input for the J-end also becomes activated.
Vertical Offset: Specify the Offset in the vertical direction. "to Extreme Fiber" assigns the offset to the outer-most point. For a specific location of Offset, select "User" and enter the distance from "Centroid" to the desired Offset location. Unless the Offset is "Center-Center" the Vertical Offset can be entered as the "User" type. For a tapered (non-prismatic) section, data input for the J-end also becomes activated.
Note 1
When Offset distance is specified, a positive (+) sign applies to Center-to-outward for Centroid reference and Extreme-to-inward for Extreme Fiber reference.
User Offset Reference: When section offset distance is specified as the "User" type, define the reference location.
Centroid: Specify the offset distance relative to the centroid of the section.
Extreme Fiber(s): Specify the offset distance relative to Left/Right & Top/Bottom.
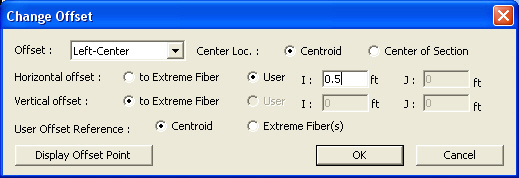
Note 2
When User type is specified, the Offset distance and direction are entered relative to Centroid irrespective of the Center option (Centroid or Center of Section). For example, specifying "Offset: Left-Center", "Center Loc.: Center of Section" and "Horizontal offset: 0.5 " User type" will result in an Offset 0.5" to the left of the Centroid. And if the Offset option is "Left-Center" and the Center option is Center of Section the User type for Horizontal offset becomes activated and the User type for Vertical offset becomes inactivated. The Horizontal offset defined as User type here becomes the Centroid, and the Vertical offset fixed to Center becomes the "Center of Section"
Note 3
When FCM Wizard is used, and "Apply the Centroid of Pier Table Section Option" is selected, the node locations of the girder will be changed as follows:
Offset: Center-Top
User Offset Reference: Extreme Fiber(s)
Vertical Offset: User, Offset Distance (i & j) = Pier Table section height-Centroid of Pier Table section
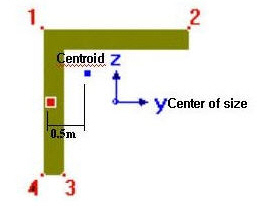
Note 4 Usage tip of Section Offset
Internal process of section offset
A beam element is defined by two nodes and a line connecting the two nodes. This line becomes a reference line representing the beam element, which usually coincides with the neutral axis of the beam element. If a section offset is assigned to a section, the neutral axis of the member shifts by the specified offset distance, and the element reference line is placed at the offset location. The reference line is used for selecting the element, assigning loads, displaying member forces, etc. The offset of the neutral axis of the member relative to the reference line in turn is reflected in analysis as shown in the figure (c) below.
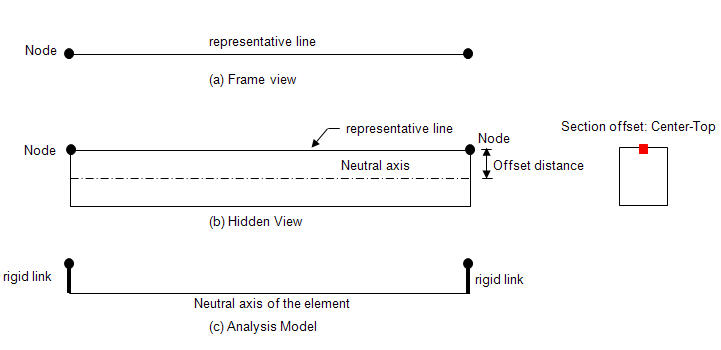
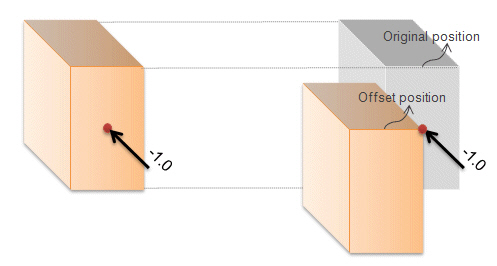
1. Nodal Load
When an offset is assigned to a section, a nodal load remains applied to the corresponding node regardless of the offset. This results in moments due to the offset to the neutral axis as shown in the case of figure b.
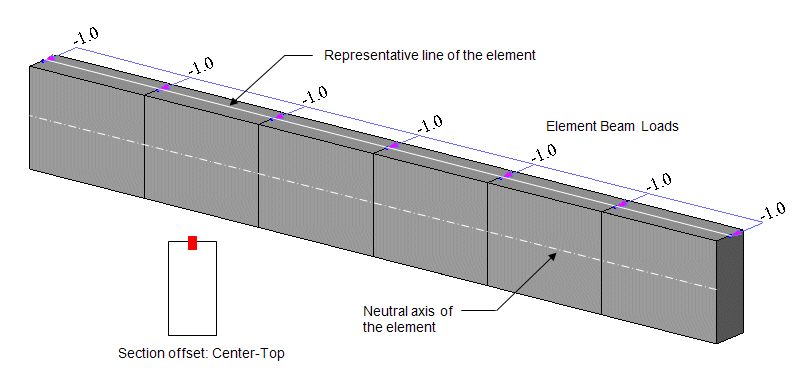
2. Element Beam Loads
Element beam load is applied to the neutral axis of the element regardless of the section offset position. In the diagram below, the element beam load is applied to the neutral axis even though the section is offset from the reference line. Therefore torsional moment from the element beam load is not induced by the offset. Note however that the element beam load is displayed on the reference line as if it is applied to the reference line, but it is actually applied to the neutral axis.
Calculation of member forces of the elements for which section offset is applied
Member forces (axial force, shear force, moment & torsion) of a beam element are calculated relative to the neutral axis. This is true even when a section offset is applied. However, the member force diagrams are displayed on the reference line. This does not mean the member forces are calculated relative to the reference line.
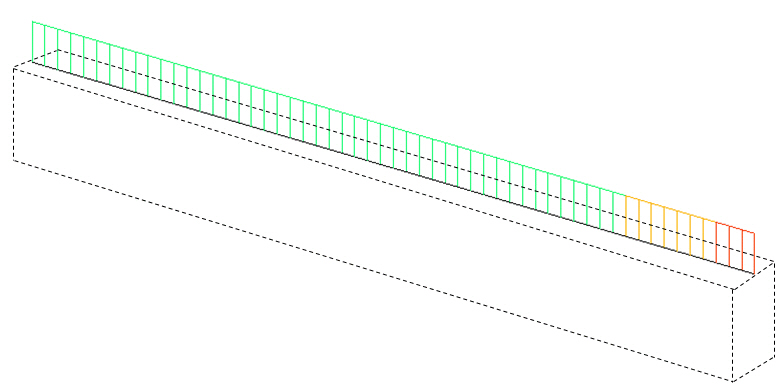
Member forces diagram when section offset is applied
Comparison between section offset and beam end offset
An offset of a section can be defined using the Beam End Offset function. For a prismatic section, a Section offset is assigned to both
i-end and j-end identically. However, Beam End Offset can assign different offsets at i-end and j-end independently. Section offset is more useful for a tapered section as opposed to Beam End Offset as shown in the figure below.
In addition, Section offset and Beam End Offset cannot be assigned simultaneously. In such a case, Section offset is ignored, and Beam End Offset only becomes effective.
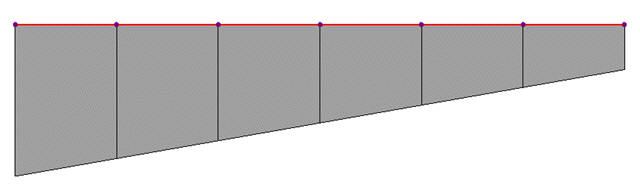
Modeling of a tapered section group when a Section offset (Center-Top) is defined
 : Display the Offset specified from the Change Offset dialog
box in the guide diagram of Section Data window.
: Display the Offset specified from the Change Offset dialog
box in the guide diagram of Section Data window.
 Consider Shear Deformation
Consider Shear Deformation
Select whether to consider
shear deformation. This option will be applicable for structural analysis,
but will not affect the effective shear areas that appear by clicking
 .
.
 Section Properties
Section Properties
Click  to display
the section property data. The section property data table is either calculated
from the main dimensions or obtained from the DB depending on the method
of data entry. [Details]
to display
the section property data. The section property data table is either calculated
from the main dimensions or obtained from the DB depending on the method
of data entry. [Details]
Area: Cross sectional area
Asy: Effective Shear Area for shear force in the element's local y-direction
It becomes inactive when Shear Deformation is not considered.
Asz: Effective Shear Area for shear force in the element's local z-direction
It becomes inactive when Shear Deformation is not considered.
Ixx: Torsional Resistance about the element's local x-axis
Iyy: Moment of Inertia about the element's local y-direction
Izz: Moment of Inertia about the element's local z-direction
Cyp: Distance from the section's neutral axis to the extreme fiber of the element in the local (+)y-direction
Cym: Distance from the section's neutral axis to the extreme fiber of the element in the local (-)y-direction
Czp: Distance from the section's neutral axis to the extreme fiber of the element in the local (+)z-direction
Czm: Distance from the section's neutral axis to the extreme fiber of the element in the local (-)z-direction
Qyb: Shear Coefficient for the shear force applied in the element's local z-direction
Qzb: Shear Coefficient for the shear force applied in the element's local y-direction
Peri: O: Total perimeter of the section
Peri: I: Inside perimeter length of a hollow section
y1, z1: Distance from the section's neutral axis to the Location 1 (used for computing combined stress)
y2, z2: Distance from the section's neutral axis to the Location 2 (used for computing combined stress)
y3, z3: Distance from the section's neutral axis to the Location 3 (used for computing combined stress)
y4, z4: Distance from the section's neutral axis to the Location 4 (used for computing combined stress)
Zyy: Plastic Section Modulus about the element local y-direction
Zzz: Plastic Section Modulus about the element local z-direction
Note 1
All the above section property data except for Area and Peri are required for beam elements.
Note 2
The shear deformations are neglected if the effective shear areas are not specified. Cyp, Cym, Czp and Czm are used to calculate the bending stresses. Qyb and Qzb are used to calculate the shear stresses. Peri is used to calculate the Painting Area.
Note 3
Zyy and Zzz are used to calculate the strength for pushover analysis when Value Type Steel Section has been assigned Design > Pushover Analysis > Define Hinge Properties.
 Revision of Ver.7.4.1
Revision of Ver.7.4.1Note
4
Element Stiffness data
Sections can be defined by the stiffness data entries even if the section dimensions (H, B1, ... , etc.) are not entered.
The cross-sectional area of a member is used to compute axial stiffness and stress when the member is subjected to a compression or tension force. Figure 1 illustrates the calculation procedure.
Cross-sectional areas could be reduced due to member openings and bolt or rivet holes for connections. midas does not consider such reductions. Therefore, if necessary, the user is required to modify the values using the option 2 above and his/her judgment.
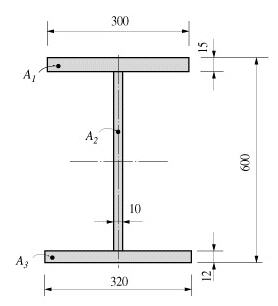
Area = +dA = A1 + A2 + A3
= (300 x 15) + (573 x 10) + (320 x 12)
= 14070
<Figure 1> Example of cross-sectional area calculation
Effective Shear Areas (Asy, Asz)
The effective shear areas of a member are used to formulate the shear stiffness in the y- and z-axis directions of the cross-section. If the effective shear areas are omitted, the shear deformations in the corresponding directions are neglected.
When midas computes the section properties by the option 1 or 3, the corresponding shear stiffness components are automatically calculated. Figure 2 outlines the calculation methods.
Asy: Effective shear area in the ECS y-axis direction
Asz: Effective shear area in the ECS z-axis direction
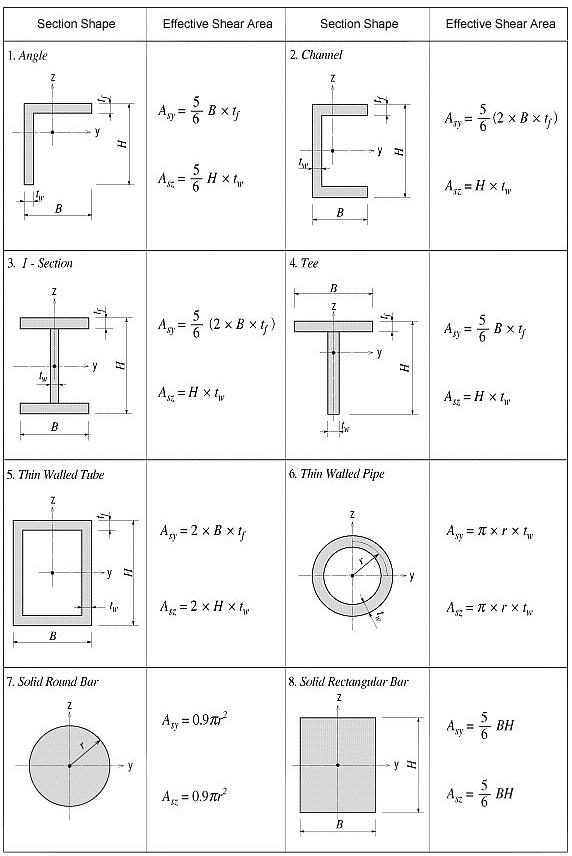
<Figure 2> Effective Shear Area calculations
Torsional resistance refers to the stiffness resisting torsional moments. It is expressed as
<Eq. 1>
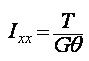
where,
Ixx: Torsional Constant
T: Torsional moment or torque
G: Shear Modulus of Elasticity
еш : Angle of twist
The torsional stiffness expressed in Eq. 1 must not be confused with the polar moment of inertia that determines the torsional shear stresses. However, they are identical to one another in the cases of circular or thick cylindrical sections.
No general equation exists to satisfactorily calculate the torsional resistance applicable for all section types. The calculation methods widely vary for open and closed sections and thin and thick thickness sections.
For calculating the torsional resistance of an open section, an approximate method is used; the section is divided into several rectangular sub-sections and then their resistances are summed into a total resistance, Ixx, calculated by the equation below.
<Eq. 2>
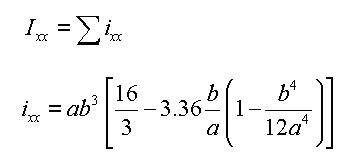
for a e b
where,
Ixx: Torsional resistance of a (rectangular) sub-section
2a: Length of the longer side of a sub-section
2b: Length of the shorter side of a sub-section
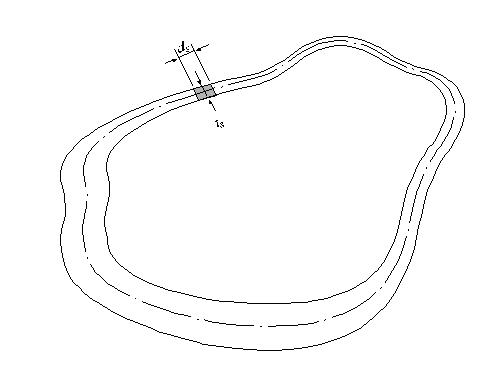
Figure 3 illustrates the equation for calculating the torsional resistance of a thin walled, tube-shaped, closed section.
<Eq. 3>
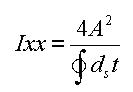
where,
A: Area enclosed by the mid-line of the tube
ds: Infinitesimal length of thickness centerline at a given point
t: Thickness of tube at a given point
For those sections such as bridge box girders, which retain the form of thick walled tubes, the torsional stiffness can be obtained by combining the above two equations, Eq. 1 and Eq. 3.
Torsional
resistance: 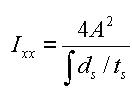
Shear stress at a given point: 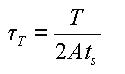
Thickness of tube at a given point:
<Figure 3> Torsional resistance of a thin walled, tube-shaped, closed section
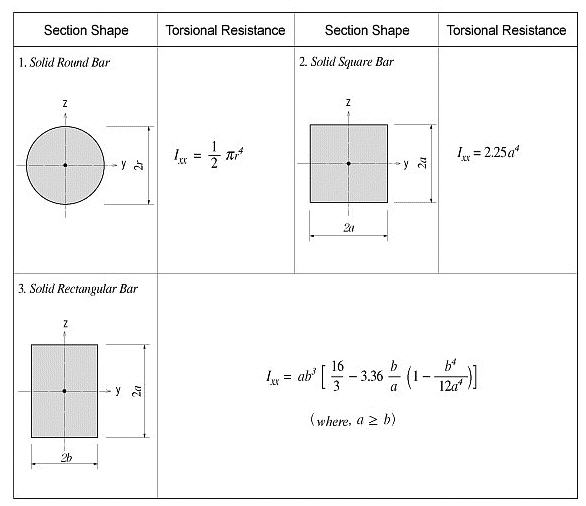
<Figure 4> Torsional resistance of solid sections

<Figure 5> Torsional resistance of thin walled, closed sections
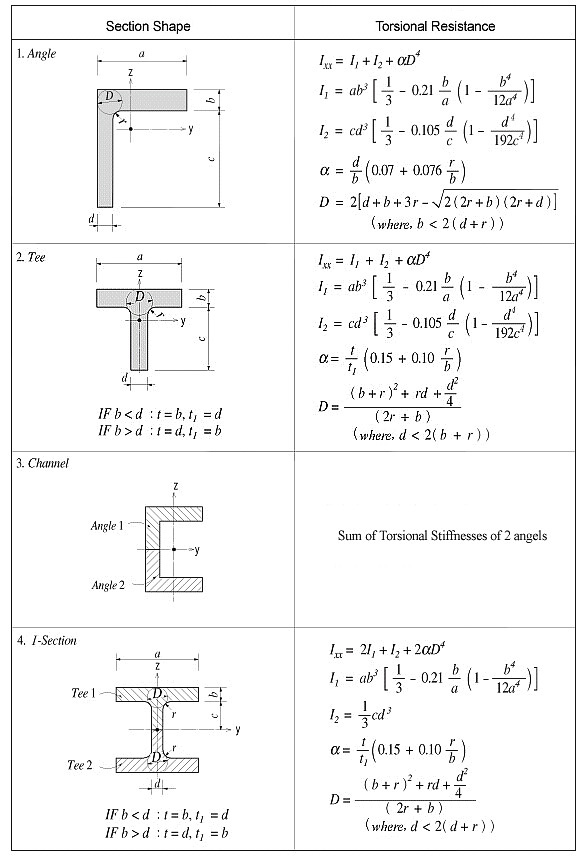
<Figure 6> Torsional resistance of thick walled, open sections
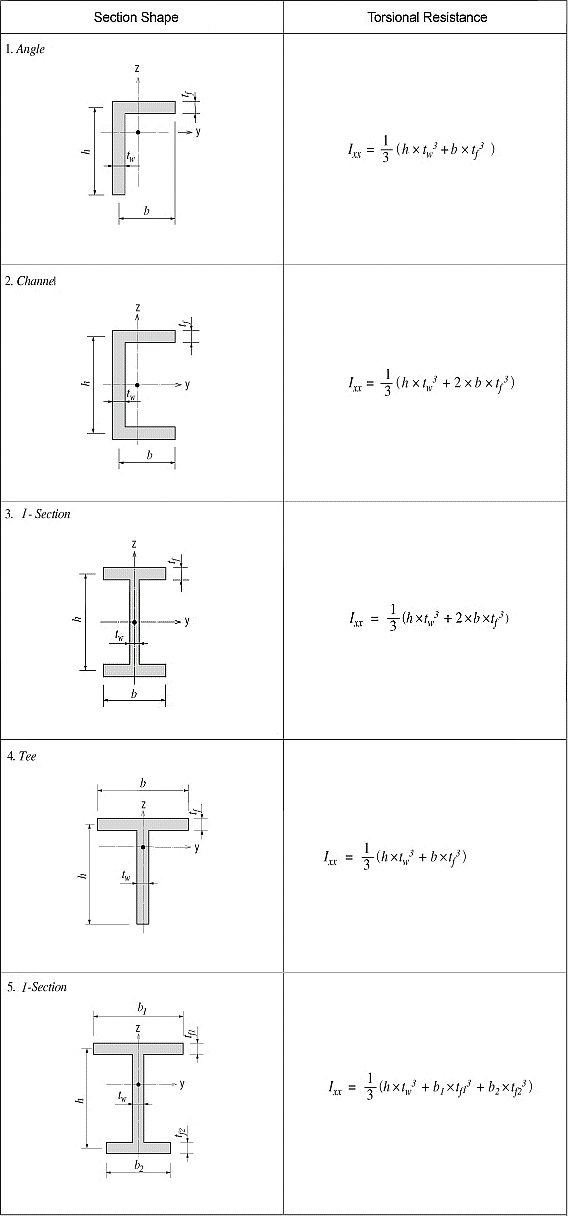
<Figure 7> Torsional resistance of thin walled, open sections
In practice, combined sections often exist. A combined built-up section may include both closed and open sections. In such a case, the stiffness calculation is performed for each part, and their torsional stiffnesses are summed to establish the total stiffness for the built-up section.
For example, a double I-section shown in Figure 8(a) consists of a closed section in the middle and two open sections, one on each side.
The torsional resistance of the closed section (hatched part)
<Eq. 4>
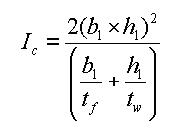
The torsional resistance of the open sections (unhatched parts)
<Eq. 5>
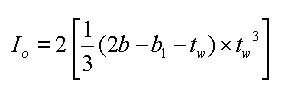
The total resistance of the built-up section
<Eq. 6>
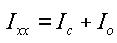
Figure 8(b) shows a built-up section made up of an I-shaped section reinforced with two web plates, forming two closed sections. In this case, the torsional resistance for the section is computed as follows:
If the torsional resistance contributed by the flange tips is negligible relative to the total section, the torsional property may be calculated solely on the basis of the outer closed section (hatched section) as expressed in Eq. 7.
<Eq. 7>
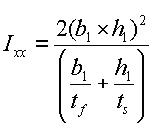
If the torsional resistance of the open sections is too large to ignore, then it should be included in the total resistance.
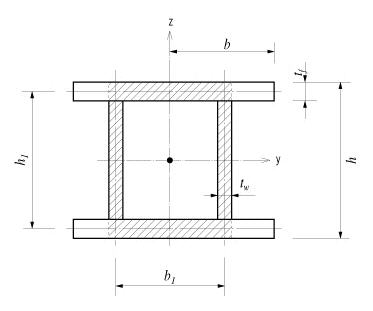
(a) Section consisted of closed and open sections
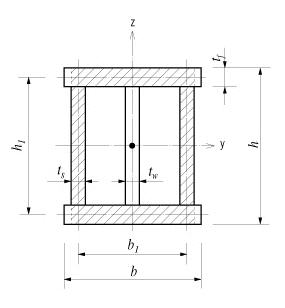
(b) Section consisted of two closed sections
<Figure 8> Torsional resistance of built-up sections
Area Moment of Inertia (Iyy, Izz)
The area moment of inertia is used to compute the flexural stiffness resisting bending moments. It is calculated relative to the centroid of the section.
Area moment of inertia about the ECS y-axis
<Eq. 8>
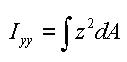
-Area moment of inertia about the ECS z-axis
<Eq. 9>
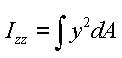
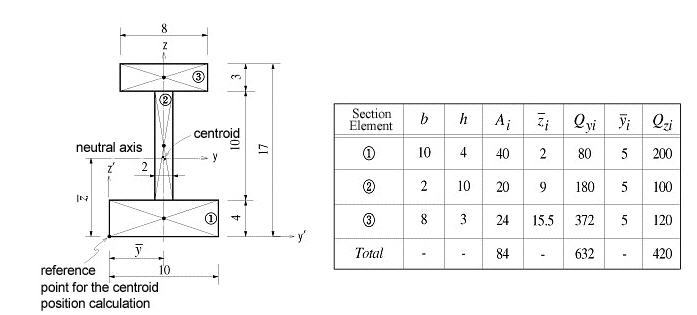
 : area
: area
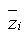 : distance from the reference
point to the centroid of the section element in the z-axis direction
: distance from the reference
point to the centroid of the section element in the z-axis direction
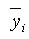 : distance from the reference
point to the centroid of the section element in the y-axis direction
: distance from the reference
point to the centroid of the section element in the y-axis direction
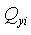 : first moment of area
relative to the reference point in the y-axis direction
: first moment of area
relative to the reference point in the y-axis direction
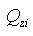 : first moment of area
relative to the reference point in the z-axis direction
: first moment of area
relative to the reference point in the z-axis direction
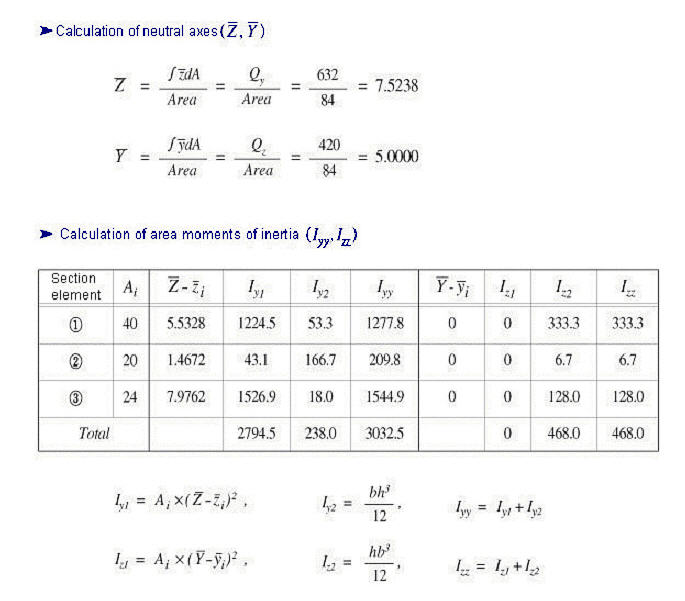
<Figure 9> Example of calculating area moments of inertia
Area Product Moment of Inertia (Iyz)
The area product moment of inertia is used to compute stresses for non-symmetrical sections, which is defined as follows:
<Eq. 10>
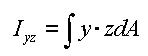
Sections that have at least one axis of symmetry produce Iyz=0. Typical symmetrical sections include I, pipe, box, channel and tee shapes, which are symmetrical about at least one of their local axes, y and z. However, for non-symmetrical sections such as angle shaped sections, where Iyz`0, the area product moment of inertia should be considered for obtaining stress components.
The area product moment of inertia for an angle is calculated as shown in Figure 10.
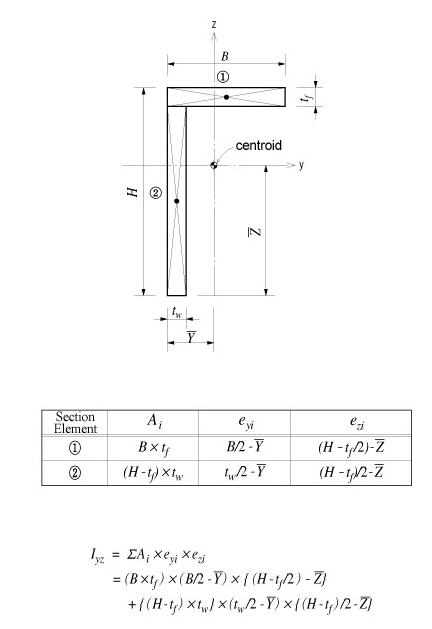
<Figure 10> Area product moment of inertia for an angle
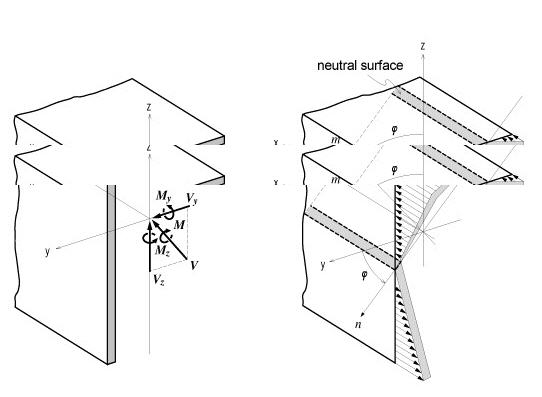
<Figure 11> Bending stress distribution of a non-symmetrical section
The neutral axis represents an axis along which bending stress is 0 (zero). As illustrated in the right-hand side of Figure 11, the n-axis represents the neutral axis, to which the m-axis is perpendicular. Since the bending stress is zero at the neutral axis, the direction of the neutral axis can be obtained from the relation defined as
<Eq. 11>
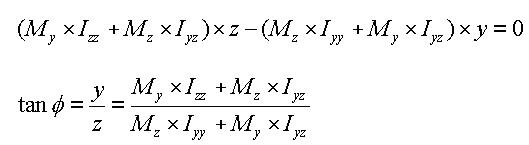
The following represents a general equation applied to calculate the bending stress of a section:
<Eq. 12>
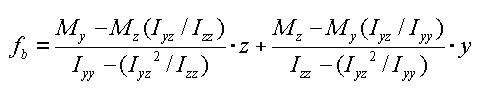
In the case of an I shaped section, Iyz=0, hence the equation can be simplified as:
<Eq. 13>
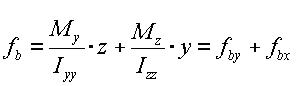
where,
Iyy: Area moment of inertia about the ECS y-axis
Izz: Area moment of inertia about the ECS z-axis
Iyz: Area product moment of inertia
y: Distance from the neutral axis to the location of bending stress calculation in the ECS y-axis direction
z: Distance from the neutral axis to the location of bending stress calculation in the ECS z-axis direction
My: Bending moment about the ECS y-axis
Mz: Bending moment about the ECS z-axis
The general expressions for calculating shear stresses in the ECS y and z-axes are:
<Eq. 14>
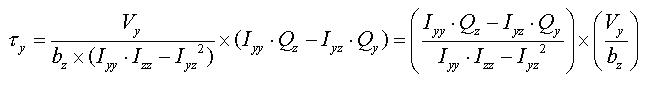
<Eq. 15>
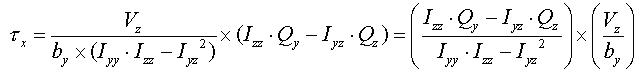
where,
Vy: Shear force in the ECS y-axis direction
Vz: Shear force in the ECS z-axis direction
Qy: First moment of area about the ECS y-axis
Qz: First moment of area about the ECS z-axis
by: Thickness of the section at which a shear stress is calculated, in the direction normal to the ECS z-axis
bz: Thickness of the section at which a shear stress is calculated, in the direction normal to the ECS y-axis
The first moment of area is used to compute the shear stress at a particular point on a section. It is defined as follows:
<Eq. 16>
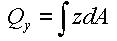
<Eq. 17>
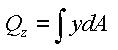
When a section is symmetrical about at least one of the y and z-axis, the shear stresses at a particular point are:
<Eq. 18>
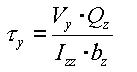
<Eq. 19>
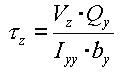
where,
Vy: Shear force acting in the ECS y-axis direction
Vz: Shear force acting in the ECS z-axis direction
Iyy: Area moment of inertia about the ECS y-axis
Izz: Area moment of inertia about the ECS z-axis
by: Thickness of the section at the point of shear stress calculation in the ECS y-axis direction
bz: Thickness of the section at the point of shear stress calculation in the ECS z-axis direction
Shear Factor for Shear Stress (Qyb, Qzb)
The shear factor is used to compute the shear stress at a particular point on a section, which is obtained by dividing the first moment of area by the thickness of the section.
<Eq. 20>
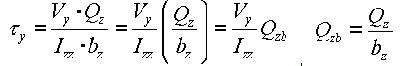
<Eq. 21>
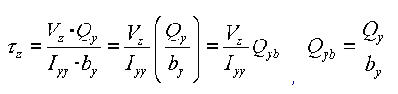
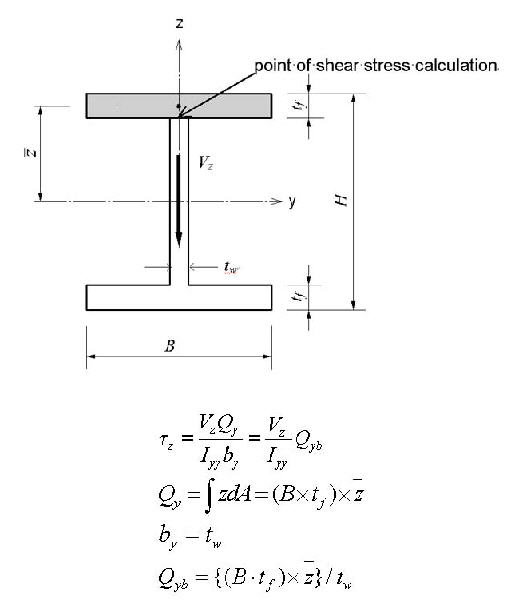
<Figure 12> Example of calculating a shear factor
Stiffness of Composite Sections
midas calculates the stiffness for a full composite action of structural steel and reinforced concrete. Reinforcing bars are presumed to be included in the concrete section. The composite action is transformed into equivalent section properties.
The program uses the elastic moduli of the steel (Es) and concrete (Ec) defined in the SSRC79 (Structural Stability Research Council, 1979, USA) for calculating the equivalent section properties. In addition, the Ec value is decreased by 20% in accordance with the EUROCODE 4.
- Equivalent cross-sectional area
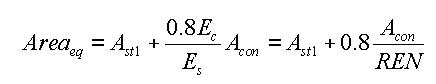
- Equivalent effective shear area
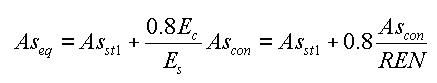
- Equivalent area moment of inertia
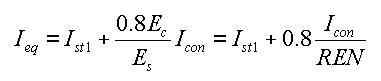
where,
Ast1: Area of structural steel
Acon: Area of concrete
Asst1: Effective shear area of structural steel
Ascon: Effective shear area of concrete
Ist1: Area moment of inertia of structural steel
Icon: Area moment of inertia of concrete
REN: Modular ratio (elasticity modular ratio of the structural steel to the concrete, Es/Ec)
 Revision of Ver.7.4.1
Revision of Ver.7.4.1
- Equivalent torsional coefficient
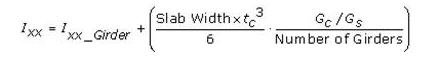
 Revision of Ver.7.4.1
Revision of Ver.7.4.1Note 5
Determining the positions of y1~4, z1~4 of a section imported from SPC [Details]
1. Divide the section into four quadrants.
2. Assign the positions furthermost from the centroid in each quadrant for checking stresses.
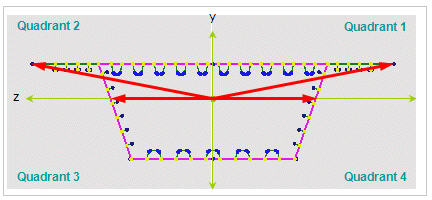
If the webs of a section are extensively sloped as in the above diagram, the points furthermost from the centroid may not be the lowest points of the section. Use caution that the stress checking positions of quadrants 3 & 4 may be selected differently from the expectation.
 Section Type
Section Type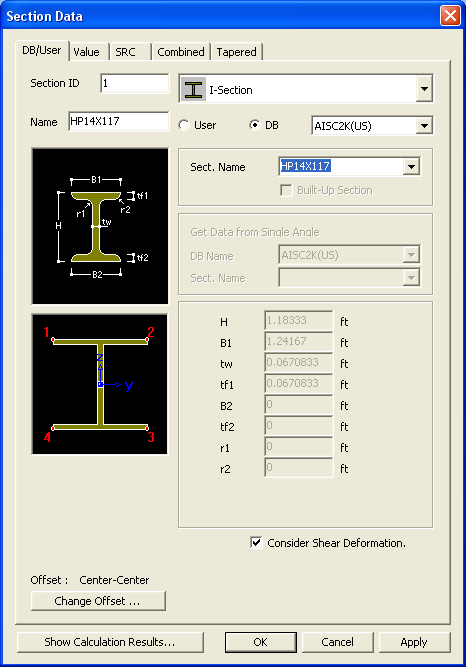
The section data can be entered by the following 2 methods in the dialog box:
1. Select a section from the DB (database) of the standard sections for a country.
2. Enter the main dimensions of a standardized section shape.
Section Shape List: Select a section shape (Angle, Channel, H-Section, T-Section, Box, Pipe, Double Angle, Double Channel, Solid Rectangle, Solid Round, Octagon, Solid Octagon, R-Octagon, Track, Solid Track, Half Track, Cold Formed Channel & U-Rib).
User: Enter the main dimensions of a standardized section shape.
H, B1, ...: Refer to the dimension information diagram in the dialog box.
DB: Select a section from the DB of the standard sections for a country.
AISC2K(US): American Institute of Steel Construction, 2000 US Unit : lb, in
AISC2K(SI): American Institute of Steel Construction, 2000 SI Unit : kN, m, mm
AISC: American Institute of Steel Construction
CISC02(US): Canadian Institute of Steel Construction (US Unit : lb, in)
CISC02(SI): Canadian Institute of Steel Construction (SI Unit : kN, m, mm)
BS(S): British Standard
Note
BS indicates BS4-1 revised prior to 1993.
BS4 - 93: British Standard / BS 4-1 : 1993
DIN(S): Deutches Institut fur Normung e.v
JIS2K : Japanese Industrial Standards 2000
JIS: Japanese Industrial Standards
KS: Korean Industrial Standards
GB-YB: Guojia Biao Zhun-Yejin Bu Biao Zhun
Pacific(SI): Bentley Pacific Standards (SI Unit : kN, m, mm)
IS84: Indian Standards
CNS91: Taiwan Standards
Sect. Name: Enter directly a DB section name or select a desired DB from the Section list. When the section name is directly entered, it must correspond to the format of the DB section names.
Ex) AISC: W36x280, BS: UB 406x178x54, DIN: HD400x288
Note
When specifying Double Angle or Double Channel sections, assign the sectional
shape in the list and select User. Then, select DB and Sect. Name from
Get Data from Single Angle (or Channel) or directly enter the main dimensions
of the section.
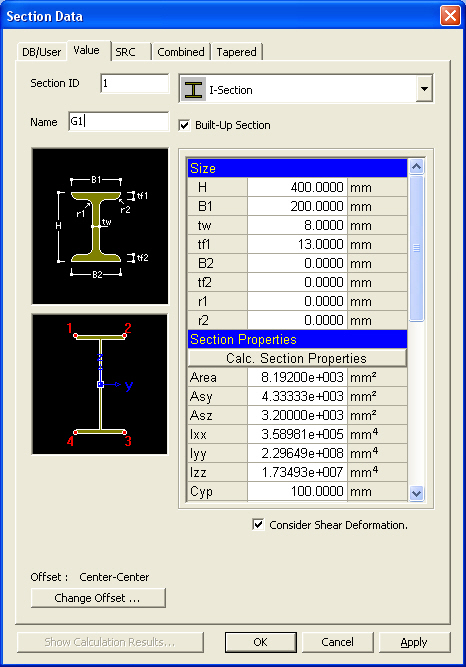
The section data can be entered by the following 3 methods in the dialog box:
1. Select a section from the DB (database) of the standard sections for a country.
2. Enter the main dimensions of a standardized section shape.
3. Import a section generated from SPC module.
Section Shape List: Assign a section shape to use.
Built-Up Section: Fabricated section
Note
Check in the case of a built-up section and leave it blank in the case
of a rolled steel section. The data is referred to for strength verification
for steel members and compiling material quantities in BOM.
Size
H, B1, ...: Refer to the diagram denoting section dimensions in the dialog box.
The structure can be analyzed only with the stiffness data even if the section dimensions are not specified.
Section Properties
The main section dimensions entered in Size are used to calculate and display the section stiffness.
Area: Cross sectional area
Asy: Effective Shear Area for shear force in the element's local y-direction
It becomes inactive when Shear Deformation is not considered.
Asz: Effective Shear Area for shear force in the element's local z-direction
It becomes inactive when Shear Deformation is not considered.
Ixx: Torsional Resistance about the element's local x-axis
Iyy: Moment of Inertia about the element's local y-direction
Izz: Moment of Inertia about the element's local z-direction
Cyp: Distance from the section's neutral axis to the extreme fiber of the element in the local (+)y-direction
Cym: Distance from the section's neutral axis to the extreme fiber of the element in the local (-)y-direction
Czp: Distance from the section's neutral axis to the extreme fiber of the element in the local (+)z-direction
Czm: Distance from the section's neutral axis to the extreme fiber of the element in the local (-)z-direction
Qyb: Shear Coefficient for the shear force applied in the element's local z-direction
Qzb: Shear Coefficient for the shear force applied in the element's local y-direction
Peri:O: Total perimeter of the section
Peri:I: Inside perimeter length of a hollow section
Note
The value of Peri:I is '0' for an I-shaped section since the section is
not hollow.
Cent:y: Centroidal distance in ECS y-axis
Cent:z: Centroidal distance in ECS z-axis
y1, z1: Distance from the section's neutral axis to the Location 1 (used for computing combined stress) The user may specify the location of the stress display.
y2, z2: Distance from the section's neutral axis to the Location 2 (used for computing combined stress) The user may specify the location of the stress display.
y3, z3: Distance from the section's neutral axis to the Location 3 (used for computing combined stress) The user may specify the location of the stress display.
y4, z4: Distance from the section's neutral axis to the Location 4 (used for computing combined stress) The user may specify the location of the stress display.
Zyy: Plastic Section Modulus about the element local y-direction
Zzz: Plastic Section Modulus about the element local z-direction
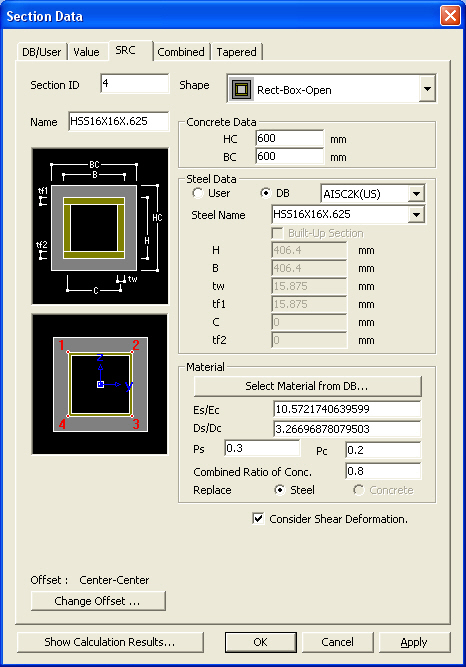
Section - SRC dialog box
Enter the section property data for steel RC composite members in the dialog box.
Shape: Assign a section shape to use.
Note
New Cross I Section and Combined T-Section were incorporated.
ConcreteData: Enter the outer dimensions of the RC section of a steel-encased concrete section.
Steel Data: Enter the steel section data.
User: Enter the main dimensions of a standardized section shape.
H, B1, ...: Refer to the dimension information diagram in the dialog box.
DB: Select a section from the DB of the standard sections for a country.
AISC2K(US): American Institute of Steel Construction, 2000 US Unit : lb, in
AISC2K(SI): American Institute of Steel Construction, 2000 SI Unit : kN, m, mm
AISC: American Institute of Steel Construction
CISC02(US): Canadian Institute of Steel Construction (US Unit : lb, in)
CISC02(SI): Canadian Institute of Steel Construction (SI Unit : kN, m, mm)
BS(S): British Standard
Note
BS indicates BS4-1 revised prior to 1993.
BS4 - 93: British Standard / BS 4-1 : 1993
DIN(S): Deutches Institut fur Normung e.v
JIS2K : Japanese Industrial Standards 2000
JIS: Japanese Industrial Standards
KS: Korean Industrial Standards
GB-YB: Guojia Biao Zhun-Yejin Bu Biao Zhun
Pacific(SI): Bentley Pacific Standards (SI Unit : kN, m, mm)
IS84: Indian Standards
CNS91: Taiwan Standards
Steel Name: Enter directly a DB section name or select a desired DB from the Section list. When the section name is directly entered, it must correspond to the format of the DB section names.
Ex) AISC: W36x280, BS: UB 406x178x54, DIN: HD400x288, JIS, KS: H 400x200x8/13
Material: Enter material properties for steel and concrete constituting steel RC composite sections.
Click  to select the material
properties for steel and concrete stored in the DB for a country. The
following items are automatically entered:
to select the material
properties for steel and concrete stored in the DB for a country. The
following items are automatically entered:
Es/Ec: Modulus of Elasticity Ratio of steel relative to concrete
Ds/Dc: Specific Weight (Density) Ratio of steel relative to concrete
Ps: Poisson's Ratio for steel
Pc: Poisson's Ratio for concrete
Combined Ratio of Conv.: Stiffness Reduction Factor of concrete [Default = 1.0]
Note
When RC is converted into steel for calculating the SRC section stiffness,
Conv. Stiffness Factor is applied to reduce the stiffness of RC.
Replace: Assign Steel to be the reference when calculating stiffness of a composite section
Note
midas converts RC into equivalent steel for SRC section stiffness calculation.
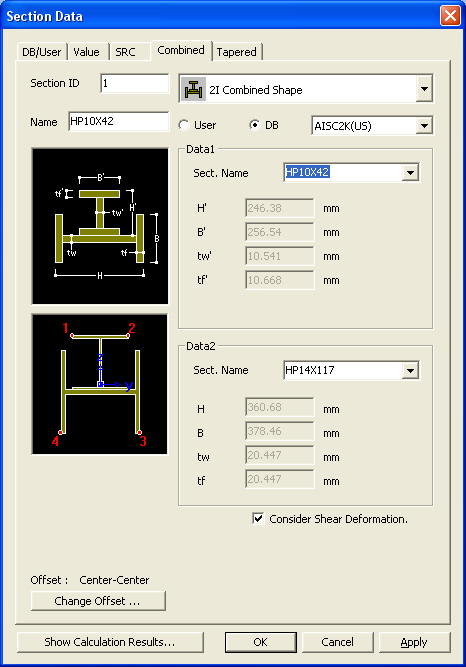
In this dialog box, enter the section properties for a combined section made up by two standard section types.
User: Enter the main dimensions of standardized section shapes.
DB: Select the sections from the DB of the standard sections for a country.
AISC2K(US): American Institute of Steel Construction, 2000 US Unit : lb, in
AISC2K(SI): American Institute of Steel Construction, 2000 SI Unit : kN, m, mm
AISC: American Institute of Steel Construction
CISC02(US): Canadian Institute of Steel Construction (US Unit : lb, in)
CISC02(SI): Canadian Institute of Steel Construction (SI Unit : kN, m, mm)
BS(S): British Standard
Note
BS indicates BS4-1 revised prior to 1993.
BS4 - 93: British Standard / BS 4-1 : 1993
DIN(S): Deutches Institut fur Normung e.v
JIS2K : Japanese Industrial Standards 2000
JIS: Japanese Industrial Standards
KS: Korean Industrial Standards
GB-YB: Guojia Biao Zhun-Yejin Bu Biao Zhun
Pacific(SI): Bentley Pacific Standards (SI Unit : kN, m, mm)
IS84: Indian Standards
CNS91: Taiwan Standards
Data 1, Data 2: Enter the section data for individual components constituting the combined section.
Sect. Name: Enter directly a DB section name or select a desired DB from the Section list. When the section name is directly entered, it must correspond to the format of the DB section names.
Ex) AISC: W36x280, BS: UB 406x178x54, DIN: HD400x288, JIS, KS: H 400x200x8/13
H, B, ...: Refer to the diagram denoting section dimensions in the dialog box.
 Revision of Ver.7.4.1
Revision of Ver.7.4.1

In this dialog box, enter the section properties for both ends of a line element to define a non-uniform section (Non-prismatic Section/ Tapered Section) of identical shape.(Refer to Note)
Section Shape List: Applicable tapered section shapes are shown below. For PSC, Composite Type or General Section of Value type, pre-defined sections can be brought in from the Section DB.
Value: Assign value when the user directly enters the section stiffness data.
Enter the section dimensions for section-i
and j separately and click  . Then, the user may modify the
auto-calculated stiffness data or directly enter the stiffness data without
entering the section dimensions.
. Then, the user may modify the
auto-calculated stiffness data or directly enter the stiffness data without
entering the section dimensions.
User: Enter the main dimensions of standardized section shapes.
DB: Select the sections from the DB of the standard sections for a country.
AISC2K(US): American Institute of Steel Construction, 2000 US Unit : lb, in
AISC2K(SI): American Institute of Steel Construction, 2000 SI Unit : kN, m, mm
AISC: American Institute of Steel Construction
CISC02(US): Canadian Institute of Steel Construction (US Unit : lb, in)
CISC02(SI): Canadian Institute of Steel Construction (SI Unit : kN, m, mm)
BS(S): British Standard
DIN(S): Deutches Institut fur Normung e.v
JIS2K : Japanese Industrial Standards 2000
JIS: Japanese Industrial Standards
KS: Korean Industrial Standards
GB-YB: Guojia Biao Zhun-Yejin Bu Biao Zhun
Pacific(SI): Bentley Pacific Standards (SI Unit : kN, m, mm)
IS84: Indian Standards
CNS91: Taiwan Standards
Section-i, Section-j: Enter directly each section name corresponding to the starting section-i and the ending section-j or select the desired DB from the section list to describe the tapered section. When the section names are directly entered, they must correspond to the DB section name format.
Ex) AISC: W36x280, BS: UB 406x178x54, DIN: HD400x288, JIS, KS: H 400x200x8/13
y Axis Variation: Dimensional variation affects the moment of inertia about the element local y-axis along the length.
z Axis Variation: Dimensional variation affects the moment of inertia about the element local z-axis along the length.
Linear: linear variation along the element local x-direction
Parabolic: parabolic variation along the element local x-direction
Cubic: cubic variation along the element local x-direction
Note 1
Calculation of section properties as per Dimensional Variation[Details]
Once the main section dimensions of both ends of a tapered section member are entered, the section properties are considered to vary from the i end (element connection node N1) to the j end (element connection node N2) along the member length. The cross sectional areas, effective shear areas and torsional resistances are assumed to vary linearly from i to j along the element local x-axis. The moments of inertia are assumed to vary linearly, parabolically or cubically depending on the directions of section changes.
For instance, in the figures below, the variations of Iyy and Izzcan be expressed as follows:
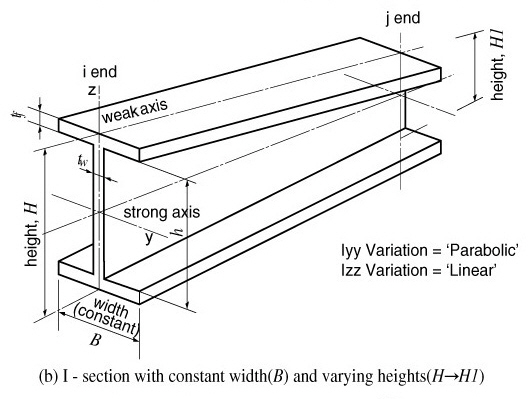
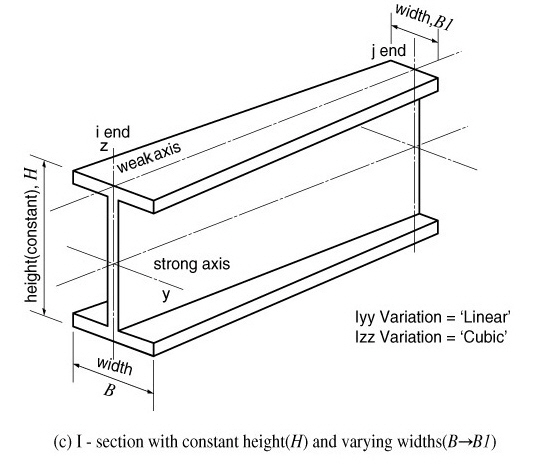
Moments of Inertia about strong and weak axes for a rectangular section <See figure below>
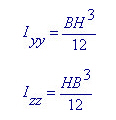
When the width (B) is constant and the height (H) varies, the moments of inertia show a cubic variation about the strong axis and a linear variation about the weak axis. Namely, Iyy Variation = 'Cubic', IzzVariation = 'Linear'.
Moments of Inertia about strong and weak axes for an I-section <See figure below>
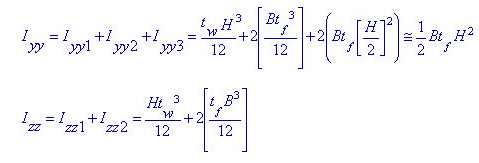
When the width (B) is constant and the height (H) varies, the moment of inertia about the strong axis shows a nearly parabolic variation if the 1st and 2nd terms are neglected in the above equation. The moment of inertia about the weak axis varies almost linearly. Hence, it is feasible to use Iyy Variation = 'Parabolic', IzzVariation = 'Linear'. On the other hand, when the height (H) is constant and the width (B) varies, the moment of inertia about the strong axis varies almost linearly and the moment of inertia about the weak axis shows a nearly cubic variation. Hence, it is feasible to use Iyy Variation = 'Linear', Izz Variation = 'Cubic'.
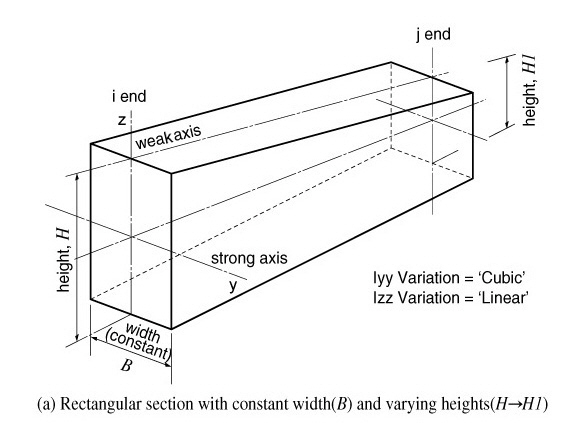
 Revision of Ver.7.4.1
Revision of Ver.7.4.1
Note 2
In the results produced in contours, diagrams and tables, dimensional variation in the axial direction affects the moment of inertia only. In Beam Detail Analysis, section properties are directly calculated at 1/4, 1/2 and 3/4 points using the shape information. As such, dimensional variation affects all the section properties (A, Asy, Asz, Ixx, Iyy & Izz).