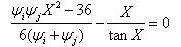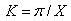Definition of Frame
|
|
|
|
|
|
Select the structural frame type (braced/unbraced) with respect to the global X- and Y-directions. Select the auto-calculation option for the effective buckling length factors for column members. |
|
|
|
|
|
|
|
From the Main Menu select Design > General Design Parameter > Definition of Frame.
From the Menu tab of the Tree Menu select Design > General Design Parameter > Definition of Frame. |
|
|
|
|
|
The following dialog box is used to enter the data:
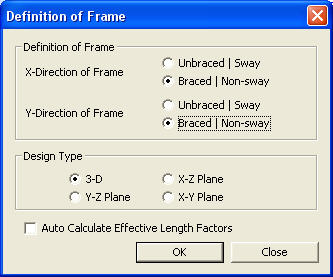
Definition of Frame dialog box
Definition of Frame
Define the type of structural frame.
X-Direction
of Frame
Y-Direction
Frame
Design Type
When members in a 3-D structure are designed, a Design Type is selected to account for only the forces in the selected plane to design the members as a 2-D frame.
3 - D: Design is carried out while accounting for all the member forces in the 3-D frame.
X - Z Plane: Design is carried out while accounting for only the member forces in the GCS X-Z plane as a 2-D frame.
Y - Z Plane: Design is carried out while accounting for only the member forces in the GCS Y-Z plane as a 2-D frame.
X - Y Plane: Design is carried out while accounting for only the member forces in the GCS X-Y plane as a 2-D frame.
Note
Auto Calculate Effective Length Factors
Select if the effective buckling length factors are to be automatically calculated.
Note
: Enter the selection and close the dialog box.
: Do not enter the selection and close the dialog box.
|
|
|