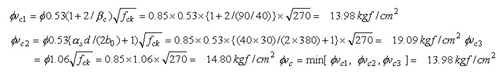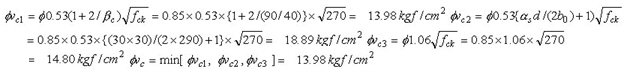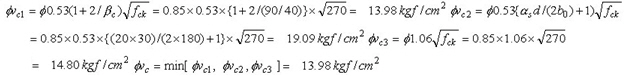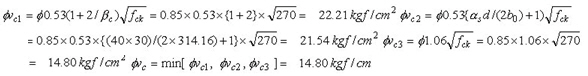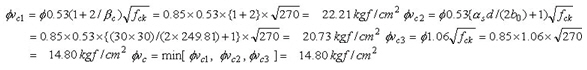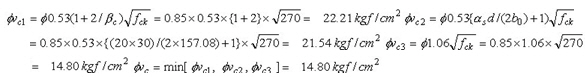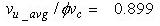Slab Shear Checking
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Produce the two-way shear (punching shear) check results at the supports of slab elements or at concentrated loads and the one-way shear check results along the user-defined Shear Check Lines. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
From the Main Menu select Design > Meshed Slab/Wall Design > Slab Shear Checking. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
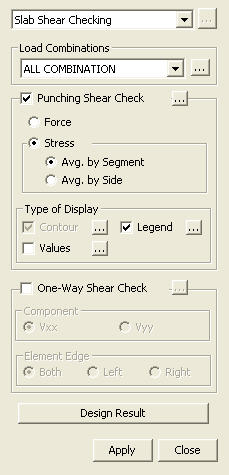
New for Gen 2010
Type of DisplayType your drop-down text here.
Define the type of display as follows:
Note Two-way shear check by Force cannot reflect the shear stress due to unbalanced moments. The user must independently check shear for floor slabs or foundation mats where significant unbalanced moments are anticipated. Shear check by Stress can reflect the shear stress due to unbalanced moments.
1. Rectangular Column
1.1 Internal Column
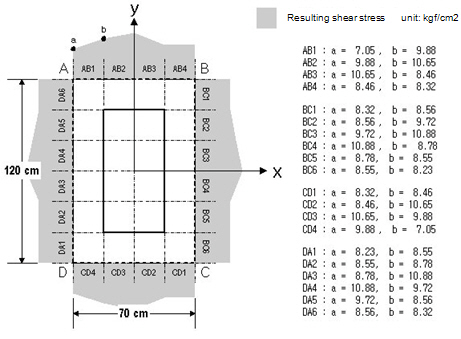
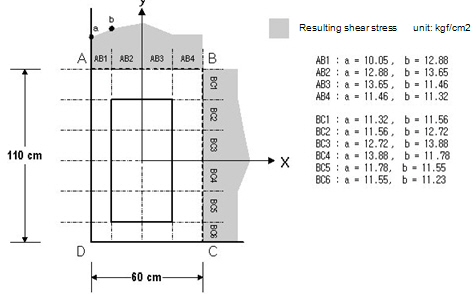
- concrete strength = 270 kgf/cm2 - column section size = 40 cm * 90 cm - slab thickness = 35 cm, rebar cover = 5 cm
① Calculate the design parameters d = 35 - 5 = 30 cm b0 = 2*70 + 2*120 = 380 cm
② Calculate the resulting shear stress
For the resulting shear stress at each location, use the average element stress or the average edge stress. unit : kgf/cm2
③ Calculate the design shear stress
④ Calculate the shear stress ratio - Check by average element stress: - Check by average edge stress:
1.2 Edge Column
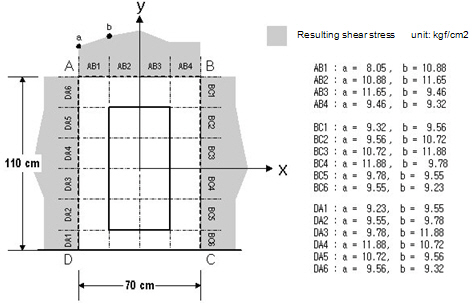
- concrete strength = 270 kgf/cm2 - column section size = 40 cm * 90 cm - slab thickness = 35 cm, rebar cover = 5 cm
① Calculate the design parameters d = 35 - 5 = 30 cm b0 = 2*110 + 70 = 290 cm
② Calculate the resulting shear stress
For the resulting shear stress at each location, use the average element stress or the average edge stress. Unit: kgf/cm2
③ Calculate the design shear stress
④ Calculate the shear stress ratio - 요소별 평균응력 검토 : - 측면별 평균응력 검토 :
1.3 Corner Column
- concrete strength = 270 kgf/cm2 - column section size = 40 cm * 90 cm - slab thickness = 35 cm, rebar cover = 5 cm
① Calculate the design parameters d = 35 - 5 = 30 cm b0 = 110 + 70 = 180 cm
② Calculate the resulting shear stress
For the resulting shear stress at each location, use the average element stress or the average edge stress. Unit: kgf/cm2
③ Calculate the design shear stress
④ Calculate the shear stress ratio - 요소별 평균응력 검토 : - 측면별 평균응력 검토 :
2. Circular Column
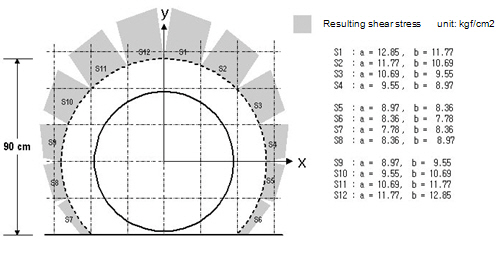
2.1 Internal Column
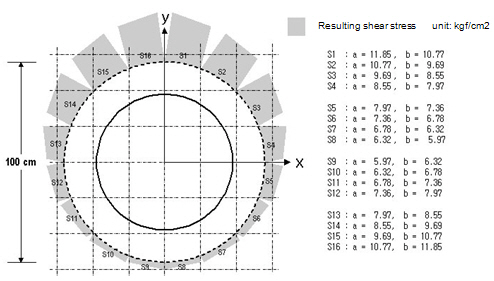
- concrete strength = 270 kgf/cm2 - Diameter of the column = 70 cm - slab thickness = 35 cm, rebar cover = 5 cm
① Calculate the design parameters d = 35 - 5 = 30 cm b0 = SUM[ Length of S1 ~ S16 ] = *100 = 314.16 cm
② Calculate the resulting shear stress For the resulting shear stress, use the average element stress. Max[ Stress of S1 ~ S16 ] = (11.85 + 10.77) / 2 = 11.31 kgf/cm2
③ Calculate the design shear stress
④ Calculate the shear stress ratio - Check by average element stress:
2.2 Edge Column
- concrete strength = 270 kgf/cm2 - Diameter of the column = 70 cm - slab thickness = 35 cm, rebar cover = 5 cm
① Calculate the design parameters d = 35 - 5 = 30 cm b0 = SUM[ Length of S1 ~ S12 ] = *100*(1 - 2*45/360) = 249.81 cm
② Calculate the resulting shear stress For the resulting shear stress, use the average element stress. Max[ Stress of S1 ~ S12 ] = (12.85 + 11.77) / 2 = 12.31 kgf/cm2
③ Calculate the design shear stress
④ Calculate the shear stress ratio - Check by average element stress:
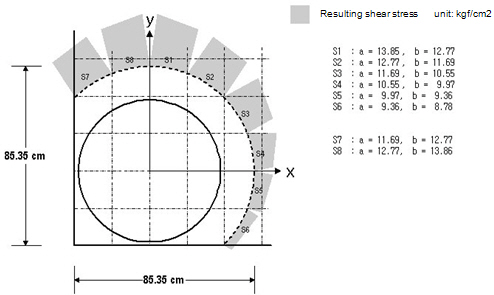
2.3 Corner Column
- concrete strength = 270 kgf/cm2 - Diameter of the column = 70 cm - slab thickness = 35 cm, rebar cover = 5 cm
① Calculate the design parameters d = 35 - 5 = 30 cm b0 = SUM[ Length of S1 ~ S8 ] = *100*(1 - 4*45/360) = 157.08 cm
② Calculate the resulting shear stress For the resulting shear stress, use the average element stress. Max[ Stress of S1 ~ S8 ] = (13.85 + 12.77) / 2 = 13.31 kgf/cm2
③ Calculate the design shear stress
④ Calculate the shear stress ratio - Check by average element stress:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
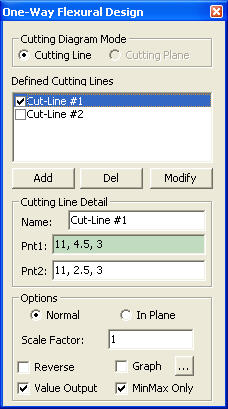

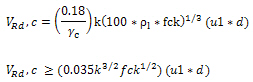
 : Add the information contained in the Cutting Line Detail
to the list of Defined Cutting Lines
: Add the information contained in the Cutting Line Detail
to the list of Defined Cutting Lines : Delete a defined cutting line
: Delete a defined cutting line : Modify a defined cutting line
: Modify a defined cutting line : Produce the flexural
checking results of wall elements in a text format.
: Produce the flexural
checking results of wall elements in a text format. : Assign the color distribution
range of contour. Using the function, specific colors for specific ranges
can be assigned.
: Assign the color distribution
range of contour. Using the function, specific colors for specific ranges
can be assigned. : Control the colors by zones
in the contour.
: Control the colors by zones
in the contour.