Definition of Frame

Select the structural frame type (braced/unbraced) with respect to the global X- and Y-directions. Select the auto-calculation option for the effective buckling length factors for column members.

From the Main Menu select Design > General > General Design Parameter > Definition of Frame.

Definition of Frame

Define the type of structural frame.

X-Direction of Frame

Select Unbraced | Sway or Braced | Non-sway frame in the global X-direction (Default = Unbraced | Sway).

Y-Direction Frame

Select Unbraced | Sway or Braced | Non-sway frame in the global Y-direction (Default = Unbraced | Sway).

 Design Type

When members in a 3-D structure are designed, a Design Type is selected to account for only the forces in the selected plane to design the members as a 2-D frame.

3 - D: Design is carried out while accounting for all the member forces in the 3-D frame.

X - Z Plane: Design is carried out while accounting for only the member forces in the GCS X-Z plane as a 2-D frame.

Y - Z Plane: Design is carried out while accounting for only the member forces in the GCS Y-Z plane as a 2-D frame.

X - Y Plane: Design is carried out while accounting for only the member forces in the GCS X-Y plane as a 2-D frame.

Note

This option may become handy when a structure with continuity in one direction is to be designed as a 2-D frame.

 Auto Calculate Effective Length Factors

Select if the effective buckling length factors are to be automatically calculated.

Note.

Auto calculation procedure for effective length factor

Reference: "Steel structures" (1982), Ballio and Mazzolani

(1)  Calculate the stiffness, S (=EI/L), otf he members which are connected to the ‘Member a’ as shown in the figure 1 below. If the joint of the flexural member is fixed or hinged as shown in the figure 2 below, the stiffness, S, is modified as below.

Fixed joint: S=(1/1.5)*EI/L

Hinge: S=(1/2.0)*EI/L

Where, E: Modulus of elasticity

I: Moment of inertia of section

L: Span length of flexural member measured from center to center of joints

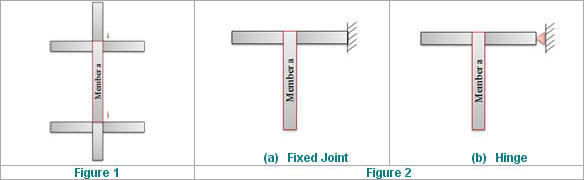
(2) Calculate Ψ and Ψ. Ψ  is the ratio of Σ(EI/lc) of compression members and Σ(EI/l) of flexural members in a plane at one end of a compression member. As shown in the figure 3 below, if the end of the compression member is fixed or hinged, Ψ  is taken as 1 or 10 respectively, If the compression member is not connected to any flexural mumber,Ψ is taken as 1000.

(3)  Calculate the solution, X, in the stability equation below.

•  Braced / Nonsway frames

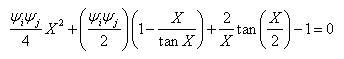
•   Unbraced / Sway frames

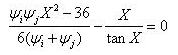
Where, Ψ: Ratio of Σ(EI/lc) of compression members to Σ(EI/l) of flexural members in a plane at one end of a

compression member.

(4)  Calculate the effective length factor, K

: Enter the selection and close the dialog box.

: Do not enter the selection and close the dialog box.