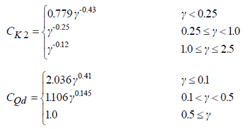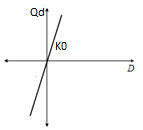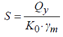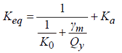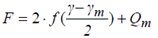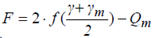Isolator (MSS)
Add, modify or delete the properties of Isolator elements.
From the Main Menu select Boundary > Link > General Link > Seismic Device Properties... > Isolator (MSS_
To
enter or add new properties of Isolator elements, click the 
button.
To
modify the properties of Isolator elements already defined, select
a name from the list of Isolator property, click the 
button and change appropriate data entries.
To
modify the properties of Isolator elements already defined, select
a name from the list of Isolator properties, click the 
button and change appropriate data entries.
Name
Enter the name of Seismic Device.
Device Type
Lead Rubber Bearings (LRB) |
Natural Rubber Bearings (NRB) |
Sliding Bearings |
|
|
|
Adjustment parameters
Enter factors to consider the performance change of isolators with rubber or lead as temperature changes. These factors are different depending on the characteristics of the product. Therefore, it is recommended to use the values provided by the manufacturer. Default value is 1 and thus the effect will not be reflected.
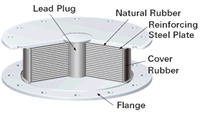
LRB Isolator Properties
Ar: Bubber Corss Section Area
Tr: Total Thickness of Rubber Laminas
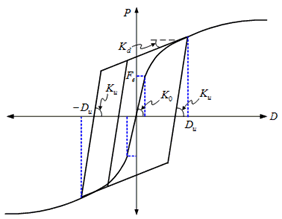
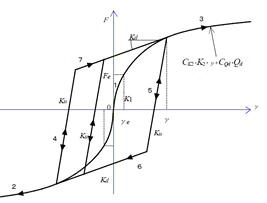
Figure 1. Force – Shear Deformation Curve |
Ko : Initial Stiffness (Ku=Ko)
K2 : 2nd Stiffness (=Kd)
Qd : Characteristic Strength of LRB
|
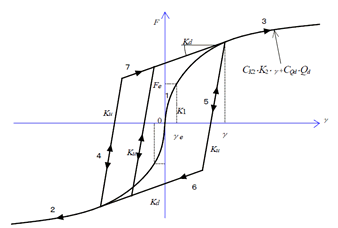
Figure 2. Force – Shear strain Curve |
γ : Shear strain of sub-shear-spring (= δ / Tr) δ : shear deformation of sub-shear-spring (=D) Tr : Total rubber thickness
CK2, CQd are correction coefficients due to horizontal secondary stiffness and strain load dependence of strain. It is represented by the following shear strain γ (γ = δ / Tr).
|
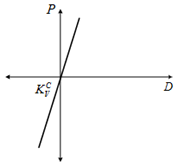
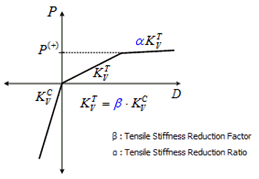
Kv(c): Vertical stiffness ( The linearity type is applied with the same stiffness for the tension and compression)
Consider
Vertical Direction Nonlinearity: Check on the option in
case of consideration of Nonlinearity.
Figure 3. linear analysis |
Figure 4. Nonlinear analysis
|
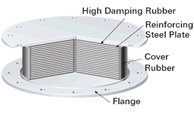
NRB Isolator Properties
Ar: Bubber Corss Section Area
Tr: Total Thickness of Rubber Laminas
|
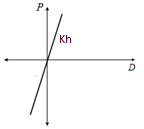
Kh : Horizontal stiffness
|
Kv(c): Vertical stiffness ( The linearity type is applied with the same stiffness for the tension and compression)
Consider
Vertical Direction Nonlinearity: Check on the option in
case of consideration of Nonlinearity.
Figure 3. linear analysis |
Figure 4. Nonlinear analysis
|
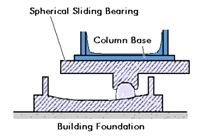
SLD Isolator Properties
As: Area of the sliding Head
Qd: Friction force
1) Case 1 : Qd = μ0 X Pi (Pi : Axial force by user input)
2) Case 2 : Qd = μ0 X P0 (P0 : Axial force by Analysis)
|
K0 : Initial stiffness Μ0 : Frictional Factor
|
|
Kv(c) : Vertical stiffness
|
Hysteresis Properties
|
|
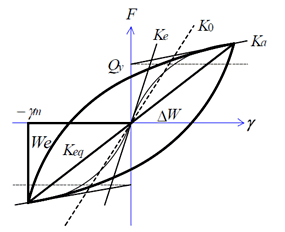
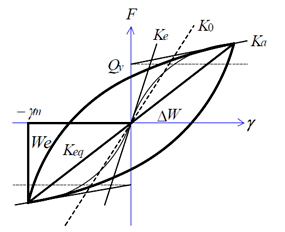
Modified Bilinear Model |
Modified HD Model (Hardin-Drnevich Model) |
|
Ka : It is calculated by γm
Ke : Initial Stiffness
Ko
:
Ko
= (Ke
–
Keq)(1+S),
Keq
:
Upward
curve:
Downward curve: |
