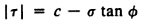Plastic Material

 

 

 

Specify a plastic material model for material nonlinear analysis.

 

 Plastic Material Models

 

      • Tresca & Von Mises

 

Appropriate for ductile metals, which exhibit Plastic Incompressibility

 

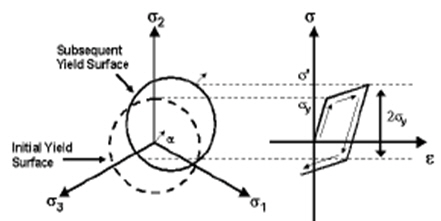
    •  Mohr-Coulomb, Drucker-Prager

 

Appropriate for brittle materials such as concrete, rock and soils, which exhibit the behavior of volumetric plastic straining

 

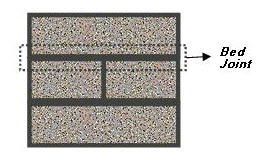
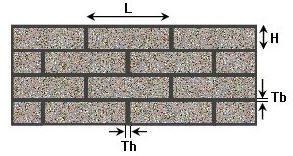
  • Masonry

 

Appropriate for the elastic analysis finding the crack positions using masonry walls (solid elements).  

 

Note
Masonry material model is applicable to plate, 4-node solid, 6-node solid, and 8-node solid elements.

 

 

 

From the Main Menu select Properties > Plastic > Plastic Material.

 

 

 

 

For new or additional material properties

 

Click in the Plastic Material dialog box and enter the following data:

 

 

 Name: Name of plastic model

 

 

  Model: Type of plastic model

 

Tresca: This yield criterion is suitable for ductile materials such as metals, which exhibit Plastic Incompressibility.

 

von Mises:This yield criterion is based on distortional strain energy and is the most widely used yield criterion for metallic materials.

 

Mohr-Coulomb:This yield criterion is a generalization of the Coulomb's friction rule and is suitable for materials such as concrete, rock and   soils, which exhibit volumetric plastic deformations.

 

Drucker-Prager:This criterion is a smooth approximation of the Mohr- Coulomb criterion and is an expansion of the von Mises criterion. This Drucker-Prager criterion is suitable for materials such as concrete, rock and soils, which exhibit volumetric plastic deformations.

 

Note

For additional details on the above 3 hardening criteria, refer to Material Nonlinear Analysis under Support>Technical Papers on MIDAS website (http://en.midasuser.com).

 

Masonry: This model is suitable for the elastic analysis finding the crack positions using masonry materials such as bricks, mortar joints, etc.

Concrete Damage:
The concrete damaged plasticity model in Midas:

 - provides a general capability for modeling concrete and other quasi-brittle materials in all types of structures
  (beams, trusses, shells, and solids);

 - is designed for applications in which concrete is subjected to monotonic, cyclic, and/or dynamic loading under low confining
  pressures;

 - can apply a different yield strengths in tension and compression

 - can consider a degradation effect of different elastic strengths in tension and compression

 

Plastic Data

 

If Tresca or Von Mises is selected, specify Initial Uniaxial (tensile) Yield Stress.

 

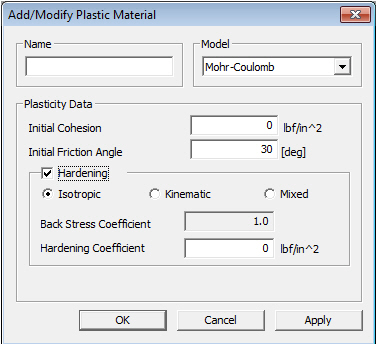
If Mohr-Coulomb or Drucker-Prager is selected, specify Initial Cohesion and Initial Friction Angle.

 

Initial Cohesion

 

Note

When normal stress is '0', Initial Cohesion is equal to the yield stress due to shear stress only.

 

Initial Friction Angle

 

Note

Initial Friction Angle, which is available only if Mohr-Coulomb or Drucker-Prager is selected as the Plastic Material Model, ranges from 0 to 90. Either use the default angle of 30 or specify the angle.

 

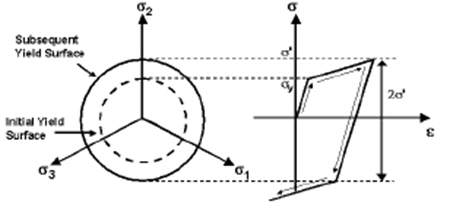
Hardening
As a material yields, hardening defines the change of yield surface with plastic straining, which is classified into the following three types.

 

Isotropic: Isotropic hardening

 

Kinematic: Kinematic hardening

 

Mixed: Mixed type hardening

 

Note

For additional details on the above 3 hardening criteria, refer to Material Nonlinear Analysis under Support>Technical Papers on MIDAS website (http://en.midasuser.com).

 

Back Stress Coefficient

 

Represents the extent of Hardening

 

'1' for Isotropic Hardening

 

'0' for Kinematic Hardening

 

between '0~1' for Mixed Hardening

 

Note

Total increment of Plastic Hardening can be expressed by Isotropic Hardening and Kinematic Hardening as follows:

 

 

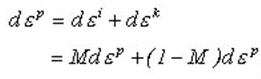
In this case, M refers to the Back Stress Coefficient, and ranges between 0 and 1.

 

Hardening Coefficient

 

Tangent stiffness of material after yielding

 

In general, after the first yielding, the Hardening Coefficient either becomes smaller than the initial tangent stiffness or becomes constant.

 

Note

In case of von Mises model (Plastic Material), the Hardening Coefficient cannot exceed the Elastic Modulus defined in Model > Property > Material.

 

 

 

When Masonry is selected

 

Brick Material Properties

 

Bed Joint Material Properties

 

Head Joint Material Properties

 

Geometry of Masonry Panel

 

 

Material Coordinate System: Orthotropic material properties are assumed for modeling a masonry structure. So it is important to define the Material Coordinate System properly.

 

Vertical : Horizontal: Select a method to define the Material Coordinate System. The Vertical and Horizontal represent the vertical axis and horizontal axis of a masonry wall respectively.

 

Global-Y : Global-X: The global-Y axis and the global-X axis must correspond to the gravitational direction and the horizontal direction of the masonry wall respectively.

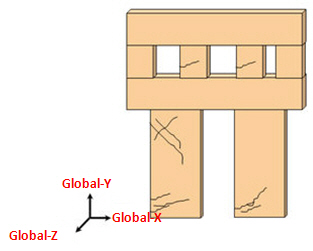
Material Coordinate System is set as Global-Y : Global-X

 

 

Local-y : Local-x: The local-y axis and the local-x axis of elements must correspond to the gravitational direction and the horizontal direction of the masonry wall respectively.

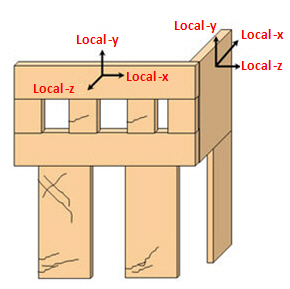
Material Coordinate System is set as Local-y : Local-x

 

 

Global-Z : Angle: The global-Z axis must correspond to the gravitational direction of the masonry wall and the horizontal direction of the wall can be defined by the angle with respect to the global-X axis on the global XY plane. The masonry wall is not necessarily located on the global X-Z plane. It can be rotated about the global-Z axis with any angle from the global-X axis.

 

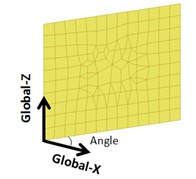
Material Coordinate System is set as Global-Z : Angle

 

Note

For masonry models where the local axes of elements are not oriented in the same direction, it is better to select Global-Y:Global-X or Global-Z:Angle as the Material Coordinate System.

 

Revision of Gen 2014 (v2.1)

 

Q1. How can you simulate nonlinear behavior of concrete with plate / solid elements ?