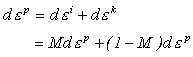塑性材料 | ||||||||
|
| ||||||||
|
| ||||||||
|
塑性解析に適用する塑性モデルを指定します。 塑性モデル
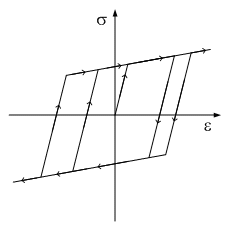
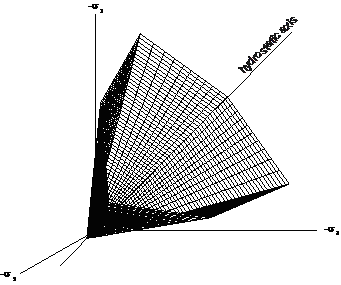
金属のように塑性非圧縮性を持つ軟性材料に適用
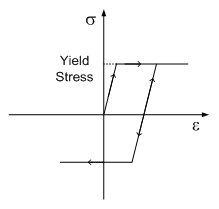
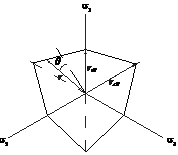
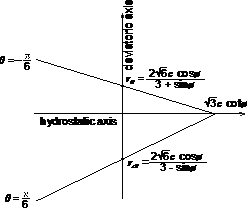
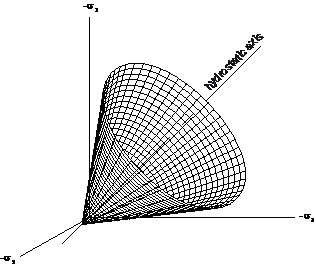
コンクリートや岩石、地盤のように体積塑性変形を起こす脆性材料に適用
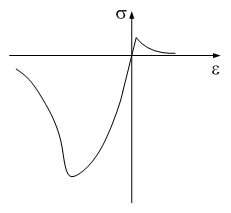
組積造(ソリッド要素)に対する塑性解析に適用 Note 組積造塑性モデルは、8節点ソリッド要素にのみ適用されます。 | ||||||||
|
| ||||||||
|
| ||||||||
|
| ||||||||
|
リボンメニュー : モデル > 材料&断面 > 材料 > 塑性材料 ツリーメニュー : メニュータブ > モデリング > 材料&断面 > 塑性材料 | ||||||||
|
| ||||||||
|
| ||||||||
|
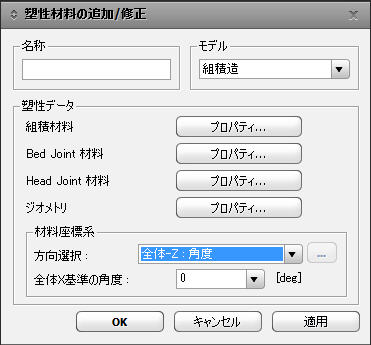
塑性材料ダイアログボックス
塑性材料の追加/修正ダイアログボックス塑性材料ダイアログボックスで、
|
|
|
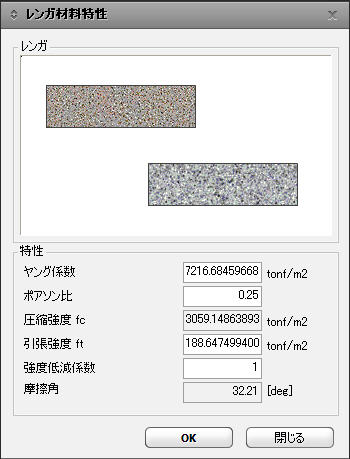
ヤング率 ポアソン比 圧縮強度, fc 引張強度, ft 剛性低減率 : ユーザーが剛性低減率を非常に小さな値に設定した場合、組積造モデルは非線形挙動をします。 同じ理由で、剛性低減率を「1」に設定した場合、組積モデルは線形挙動をします。 摩擦角 |
|
|
ヤング率 ポアソン比 圧縮強度, fc 引張強度, ft 剛性低減率 : ユーザーが剛性低減率を非常に小さな値に設定した場合、組積造モデルは非線形挙動をします。 同じ理由で、剛性低減率を「1」に設定した場合、組積モデルは線形挙動をします。 脱付着強度 |
|
|
ヤング率 ポアソン比 圧縮強度, fc 引張強度, ft 剛性低減率 : ユーザーが剛性低減率を非常に小さな値に設定した場合、組積造モデルは非線形挙動をします。 同じ理由で、剛性低減率を「1」に設定した場合、組積モデルは線形挙動をします。 脱付着強度 |
|
|
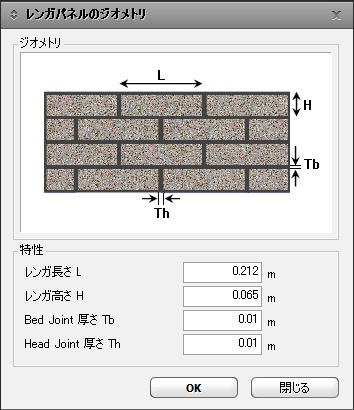
煉瓦の幅 : 煉瓦長さ 煉瓦の高さ : 煉瓦高さ Bedの厚さ, Tb : 横モルタル層の幅 Headの厚さ, Th : 縦モルタル層の幅 |
材料座標系
方向選択:組積造は直交違方性材料ですので、材料座標系の定義が重要です。
(組積造の垂直軸:組積造の水平軸で示しています。)
全体-Y:全体-X
全体Yと全体Xは、重力方向と組積造の水平方向と一致いなければなりません。
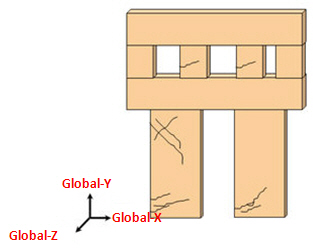
要素-y:要素-x
要素yと要素xは、重力方向と組積造の水平方向と一致いなければなりません。
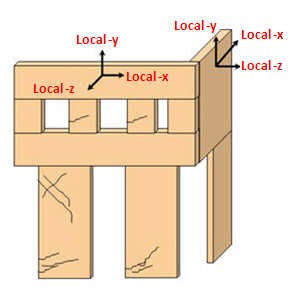
全体-Z:角度
全体Zと指定した角度は、重力方向と組積造の水平方向と一致いなければなりません。
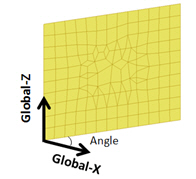
Note8
組積材料モデルは等価の直交異方性モデルですので、材料軸方向を適切に設定しなければなりません。
ですので、全体Y:全体Xより、要素yと要素xや全体Z:角度で材料座標系を指定したほうが良いです。
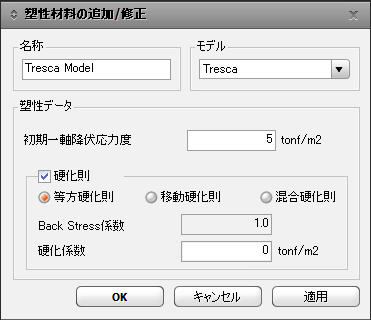
 をクリックして次の事項を入力します。
をクリックして次の事項を入力します。