断面 - 共通 | ||
|
| ||
|
| ||
|
線要素(トラス要素、引張専用要素、圧縮専用要素、ケーブル要素、ギャップ要素、フック要素、梁要素)の断面性能を入力します。 | ||
|
| ||
|
| ||
|
| ||
|
リボンメニュー : ホーム > 断面/厚さ > 梁/柱/ブレース リボンメニュー : モデリング > 材料 & 断面 > 断面 > 断面 ツリーメニュー : 2次設計タブ > 断面/厚さ > 梁/柱/ブレース | ||
|
| ||
|
| ||
|
断面データのダイアログから
材料&断面(断面)のダイアログボックス
断面リスト 既存のfn.MGBファイルに入力されている断面データが表示されます。 選択されたリスト 読み込む断面データを選択し、リストに登録します。 Note
|
|
|
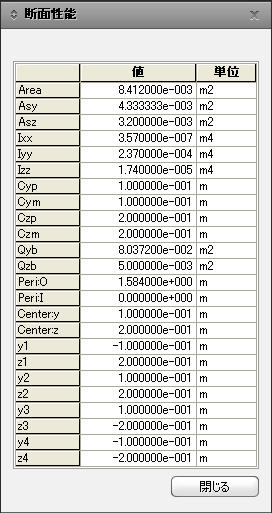
Area : 断面積 Asy : 要素座標系 y軸方向せん断力に抵抗する有効断面積。せん断変形を考慮しない場合、非アクティブ化されます。 Asz : 要素座標系 z軸方向せん断力に抵抗する有効断面積。せん断変形を考慮しない場合、非アクティブ化されます。 Ixx : 要素座標系 x軸方向のねじり剛性。 Iyy : 要素座標系 y軸方向に対する断面2次モーメント。 Izz : 要素座標系 z軸方向に対する断面2次モーメント。 Cyp : 断面の中立軸から要素座標系 (+)y軸方向最外端までの距離。 Cym : 断面の中立軸から要素座標系 (-)y軸方向最外端までの距離。 Czp : 断面の中立軸から要素座標系 (+)z軸方向最外端までの距離。 Czm : 断面の中立軸から要素座標系 (-)z軸方向最外端までの距離。 Qyb : 要素座標系 z軸方向に作用するせん断力に対するせん断係数。 Qzb : 要素座標系 y軸方向に作用するせん断力に対するせん断係数。 Peri : O : 断面外郭線の総長さ。 Peri : I : 箱またはパイプなどの断面で断面内部線の長さ。 y1、z1 : 断面の中立軸から位置1までの距離として、合成応力の計算に使用されます。 y2、z2 : 断面の中立軸から位置2までの距離として、合成応力の計算に使用されます。 y3、z3 : 断面の中立軸から位置3までの距離として、合成応力の計算に使用されます。 y4、z4 : 断面の中立軸から位置4までの距離として、合成応力の計算に使用されます。 |
Note1
上記の断面性質データの中で面積とPeriを除いたデータは線要素の中で梁要素のみ必要です。
Note2
有効断面積が入力されないとせん断変形が無視されて、Cyp, Cym, Czp, Czmは曲げ応力の計算だけ使われて、Qyb, Qzbはせん断応力を計算する時に使用されます。Periは塗装面積を計算するのに使われます。
Note 3
Zyy, Zyyは、設計>静的増分解析>静的増分ヒンジプロパティの定義で静的増分解析時に、鉄骨断面値タイプに対して強度計算時に利用される塑性断面係数です。極限の場合、Pc(圧縮) ,Pt(引張), M0(P=0の場合の曲げ強度=Fy× Zyy, Fy×Zzz)で PM-Curveを生成する時に利用されます。
Note 4
要素の剛性データ計算
断面積(Cross Sectional Area)は、部材が軸力(Axial Force)を受ける場合、これに抵抗する軸剛性(Axial Stiffness)の計算、及び部材に発生した応力度を計算するのに使用し、 その計算方法は <図 1>の通りです。
プログラムの内部で、断面積を計算したりデータベースから入力する場合には、接合部のボルト穴またはリベット穴などによる断面積の欠損は考慮しないため、必要な場合には、前述した方法 2.を用いて、ユーザーの判断により適宜に補正した断面積を入力します。
<図 1> 断面積の計算例
せん断変形用の有効せん断面積(Effective Shear Area)は、部材断面の要素座標系y軸またはz軸方向に作用するせん断力(Shear Force)に抵抗するせん断剛性(Shear Stiffness)の計算に使用します。
もし、有効せん断面積が入力されなかった場合には、該当方向のせん断変形が無視されます。
プログラム内部で断面性能を自動計算したり、データベースから入力した場合には、せん断変形用の有効せん断面積が自動計算され、その計算方法は<図 2>のようになります。
Asy : 要素座標系 y軸方向に作用するせん断力に対する有効せん断面積
Asz : 要素座標系 z軸方向に作用するせん断力に対する有効せん断面積
<図 2> 各断面の有効せん断面積
ねじり剛性は、ねじりモーメントに抵抗する剛性で、次のように定義されます。
<式 1>
ここで、
Ixx : ねじり剛性(Torsional Resistance)
T : ねじりモーメント(Torsional Moment or Torque)
θ : ねじり角度(Angle of Twist)
ねじり剛性は、上式によって定義されたねじりに対して抵抗する剛性であり、ねじりによるせん断応力度を求める断面2次極モーメント(Polar Moment of Inertia)とは異なります。(ただし、円形断面または厚肉円筒断面の場合には、ねじり剛性と断面2次極モーメントは同じになります。)
断面形状が開断面(Open Section)なのか、閉断面(Closed Section)なのかによって、ねじり剛性の計算方法が異なります。また、断面が厚肉なのか薄肉なのかによっても、計算方法が異なるため、あらゆる種類の断面に共通して適用できる一般式はありません。
開断面のねじり剛性の計算は、開断面を長方形断面に分割して下式を用いて計算し、その値を総和することによって近似的に求めることができます。
<式 2>
ただし、
a > b
ここで、
ixx : 分割断面(長方形)のねじり剛性
2a : 分割断面の長辺の長さ
2b : 分割断面の短辺の長さ
また、薄肉閉断面に対するねじり剛性の計算式は次の通りです。(<図 3> 参照)
<式 3>
ここで、
A : 断面積
dS : 任意位置における中立線の微小長さ
t : 任意位置における厚さ
また、橋梁の箱型断面のように、厚肉閉断面に対するねじり剛性は、上記の<式 1>と<式 3>の和から求めることができます。
<図 3> 薄肉閉断面のねじり剛性及びせん断応力度
<図 4> ソリッド断面のねじり剛性
<図 5> 薄肉閉断面のねじり剛性
<図 6> 厚肉開断面のねじり剛性
<図 7> 薄肉開断面のねじり剛性
2つ以上の形鋼を組合わせて1つの断面にするとき、場合によっては閉断面と開断面の両方が存在することがあります。このような場合のねじり剛性の計算は、閉断面部分と開断面部分に分けて計算した後、それぞれの値の和をとります。
例えば、ダブルH断面(Double H-Section)の場合、<図 6(a)>のように断面の中央には閉断面が形成され、フランジ両端は開断面になります。
・ 閉断面の部分(ハッチングされた部分)のねじり剛性
<式 4>
・ 開断面の部分(フランジの突出した部分)のねじり剛性
<式 5>
・ 全断面に対するねじり剛性
<式 6>
H型断面を2枚のプレートで補強する場合、<図 6(b)>のように閉断面が2つ存在し、このときのねじり剛性は次のように計算します。
フランジ両端の開断面の部分に対するねじり剛性が、全断面のねじり剛性に対して無視できる程小さな値の場合には、 H型断面の上下フランジと2枚の補強プレートによって形成される外周の閉断面に対して、下式のようにねじり剛性を計算します。
<式 7>
また、全断面を構成する断面要素の中で、開断面としてのねじり剛性が無視できない場合には、開断面に対するねじり剛性を計算して加えます。
(a) 閉断面と開断面が共に存在する場合
(b) 閉断面が2つ以上存在する場合
<図 8> 2つ以上の形鋼を組合わせた断面のねじり剛性
断面2次モーメント(Area Moment of Inertia)は、曲げモーメント(Bending Moment)に抵抗する剛性(Flexual Stiffness)を計算するのに使用し、該当断面の中立軸に対して、次式のように計算します。
・ 要素座標系y軸に対する断面2次モーメント
<式 1>
・ 要素座標系z軸に対する断面2次モーメント
<式 2>
<図 9> 断面2次モーメントの計算例
断面相乗モーメント(Area Product Moment of Inertia)は、主に非対称断面の応力度分布を計算するのに使用し、次のように定義されます。
<式 1>
H型、円筒型、箱型、溝型、及びT型断面のように、要素座標系 y軸または z軸に対して対称であるためIyz=0となります。一方、山型断面のように、要素座標系y、z軸の両軸に対して非対称であるため Iyz≠0となり、応力度分布の計算において Iyzの値を考慮する必要があることを意味します。
山型断面の断面相乗モーメントの計算方法は、<図 10>の通りです。
<図 10> 山型断面の断面相乗モーメントの計算
<図 11> 非対称断面の曲げ応力度の分布図
中立軸(Neutral Axis)は、曲げモーメントによる部材内の曲げ応力度がゼロとなる点を結ぶ軸のことを差します。<図 11>の右側の図においてn-軸が中立軸になります。m-軸は、n-軸に対して垂直な軸です。
中立軸では、曲げモーメントによる応力度がゼロになるため、次の方程式から中立軸の方向を求めることができます。
<式 2>
曲げモーメントによる断面の応力度を計算するための一般式は次の通りです。
<式 3>
もし、H型断面の場合には、Iyz =0となるので
<式 4>
ここで、
Iyy : 要素座標系 y軸に対する断面2次モーメント
Izz : 要素座標系 z軸に対する断面2次モーメント
Iyz : 断面相乗モーメント
y : 断面の中立軸から曲げ応力度を計算する位置までの要素座標系 y軸方向の距離
z : 断面の中立軸から曲げ応力度を計算する位置までの要素座標系 z軸方向の距離
Mby : 要素座標系 y軸回りの曲げモーメント
Mbz : 要素座標系 z軸回りの曲げモーメント
要素座標系 y軸及び z軸方向に作用するせん断力に対する応力度を計算するための一般式は次の通りです。
<式 5>
<式 6>
ここで、
Vy : 要素座標系 y軸方向に作用するせん断力
Vz : 要素座標系 z軸方向に作用するせん断力
Qy : 要素座標系 y軸に対する断面1次モーメント
Qz : 要素座標系 z 軸に対する断面1次モーメント
by : せん断応力度を計算する位置での要素座標系 y軸方向の断面幅
bz : せん断応力度を計算する位置での要素座標系 z軸方向の断面幅
断面1次モーメント(First Moment of Area)は、断面の任意位置でのせん断応力度を計算するのに使用し、次のように計算します。
<式 1>
<式 2>
断面が y軸または z軸に対して対称である場合、任意位置でのせん断応力度は次のように計算します。
<式 3>
<式 4>
ここで、
Vy : 要素座標系 y軸方向に作用するせん断力
Vz : 要素座標系 z軸方向に作用するせん断力
Iyy : 要素座標系 y軸に対する断面2次モーメント
Izz : 要素座標系 z軸に対する断面2次モーメント
by : せん断応力度を計算する位置での要素座標系 y軸方向の断面幅
bz : せん断応力度を計算する位置での要素座標系 z軸方向の断面幅
せん断係数は、せん断力によるせん断応力度を計算するのに使用し、部材断面においてせん断応力度を計算する位置に対する断面1次モーメントを計算位置での断面幅で除した値です。
<式 1>
<式 2>
<図 12> せん断係数の計算例
プログラムで、鉄骨-鉄筋コンクリートの合成部材の剛性は、コンクリート断面(鉄筋の断面はコンクリート断面に含まれる)と鉄骨断面が構造的に完全に合成されるものと仮定し、等価換算断面性能(Equivalent Sectional Properties)の形で考慮します。
等価換算断面性能の計算で、鋼材の弾性係数(Es)とコンクリートの弾性係数(Ec)は、鉄骨-鉄筋コンクリート規準(SSRC79(Structural Stability Research Council, 1979, USA))に明記された数値を使用し、Ecの値はEUROCODE 4により20%だけ低減した値を使用します。
・ 等価換算断面積
・ 等価換算有効せん断面積
・ 等価換算断面2次モーメント
ここで、
Ast1 : 鉄骨の断面積
Acon : コンクリートの断面積
Asst1 : 鉄骨の有効せん断面積
Ascon : コンクリートの有効せん断面積
Ist1 : 鉄骨の断面2次モーメント
Icon : コンクリートの断面2次モーメント
REN : コンクリートの弾性係数(Ec)に対する鉄骨の弾性係数(Es)の比(Es/Ec)
 をクリックし、断面データの入力タイプ別に以下のように入力します。
をクリックし、断面データの入力タイプ別に以下のように入力します。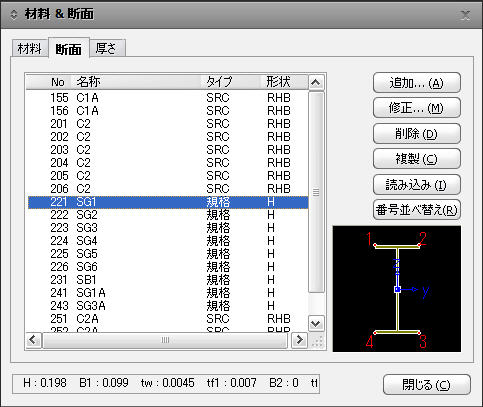
_button_06.jpg) : クリープタブ及び乾燥収縮タブからボタンをクリックして次の事項を入力します。
: クリープタブ及び乾燥収縮タブからボタンをクリックして次の事項を入力します。_button_07.jpg) : 入力した内容を確認・修正します。
: 入力した内容を確認・修正します。_button_08.jpg) : 入力した内容を削除します。
: 入力した内容を削除します。 : 入力された内容を複製します。
: 入力された内容を複製します。 : 断面データが入力されているMGBファイルを読み込みます。
: 断面データが入力されているMGBファイルを読み込みます。 : 既に入力されている断面番号を再設定します。
: 既に入力されている断面番号を再設定します。
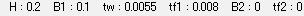 : 規格/ユーザータブから指定した場合に断面の情報が表示されます。
: 規格/ユーザータブから指定した場合に断面の情報が表示されます。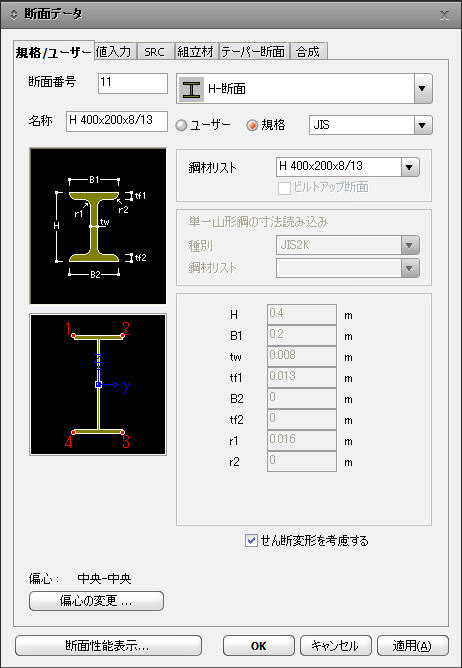
 ボタンをクリックすると断面性質の入力方法によってDBに保存された断面誠実データまたは断面主要寸法によって計算された断面性質データテーブルが現れます。
ボタンをクリックすると断面性質の入力方法によってDBに保存された断面誠実データまたは断面主要寸法によって計算された断面性質データテーブルが現れます。 "
"
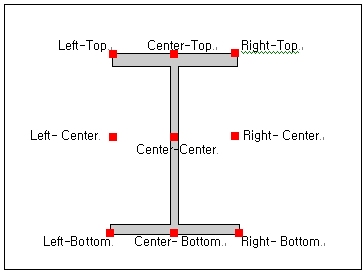
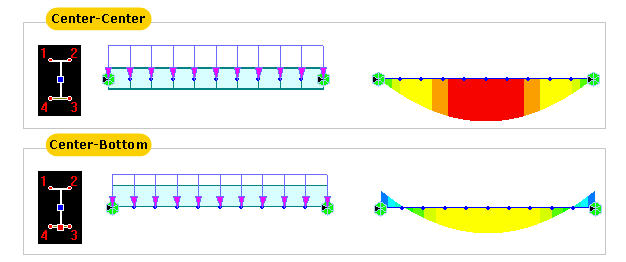
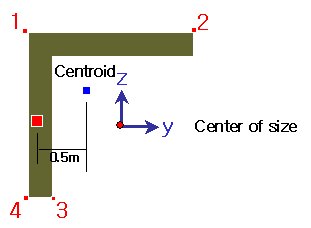
 をクリックすると、断面リスト毎に保存された断面性能データ、または直接入力された寸法によって計算された断面性能データが表示されます。
をクリックすると、断面リスト毎に保存された断面性能データ、または直接入力された寸法によって計算された断面性能データが表示されます。