塑性材料
塑性解析に適用する塑性モデルを指定します。
塑性モデル
Tresca、Von Mises
金属のように塑性非圧縮性を持つ軟性材料に適用
Mohr-Coulomb、Drucker-Prager
コンクリートや岩石、地盤のように体積塑性変形を起こす脆性材料に適用
組積造
組積造(ソリッド要素)に対する塑性解析に適用
Note
組積造塑性モデルは、8節点ソリッド要素にのみ適用されます。
リボンメニュー : モデル > 材料&断面 > 材料 > 塑性材料
ツリーメニュー : メニュータブ > モデリング > 材料&断面 > 塑性材料
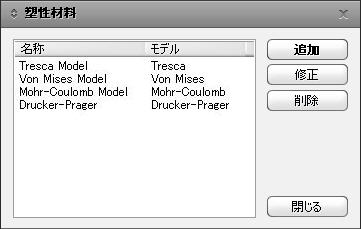
塑性材料ダイアログボックス
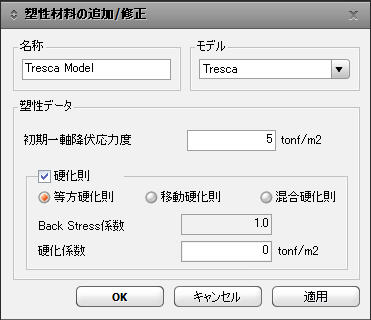
塑性材料の追加/修正ダイアログボックス
塑性材料ダイアログボックスで、 をクリックして次の事項を入力します。
をクリックして次の事項を入力します。
 名称
名称
塑性モデルの名称
 モデル
モデル
塑性モデルの種類
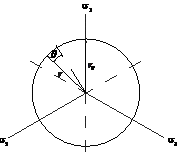
Tresca:金属のように塑性非圧縮(Plastic Incompressibility)のような軟性材料に適するモデルです。
Vob Mises:このモデルは、ひずみエネルギーを元にしたモデルで、金属によく使われるモデルです。
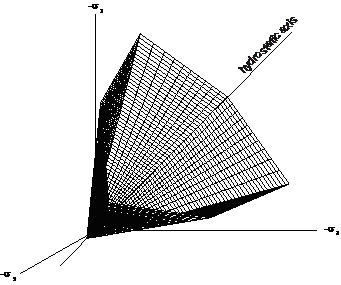
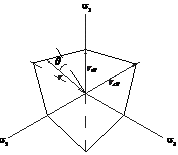
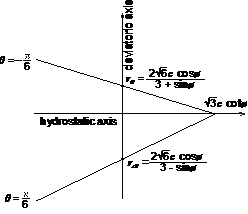
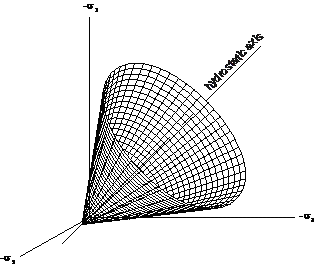
Mohr-Coulomb:Coulomb 摩擦法則が考慮されたモデルでコンクリート、地盤、岩のように体積塑性性材料に適したモデルです。
Drucker-Prager:このモデルは、 Mohr- Coulombモデルと近似で、 von Misesモデルが拡張されたモデルであり、 コンクリート、地盤、岩のように体積塑性性材料に適したモデルです。
Note1
上の4つ塑性モデルに対する詳しい内容は "Analysis & Design″マニュアル非線形解析の塑性材料モデルの部分を
参照してください。
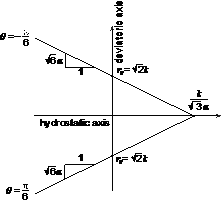
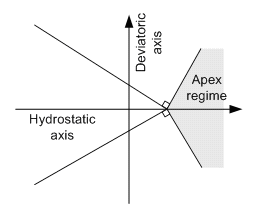
組積造 : このモデルは煉瓦などの組積造に対しての塑性解析に適したモデルです。
 塑性データ
塑性データ
Tresca、Von Misesを選択した場合
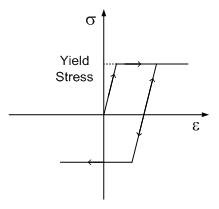
初期一軸降伏応力度 : 単一軸の引張実験による降伏応力度
Mohr-Coulomb、Drucker-Pragerを選択した場合
初期粘性値:初期粘性
Note2
Normal 応力度が'0'の場合、せん断応力度のみによる降伏応力度と同じです。
初期摩擦角:初期内部摩擦角
Note3
初期摩擦角の入力は塑性材料モデルがMohr CoulombやDrucker Pragerである場合、"0<初期摩擦角<90″の範囲で
入力可能です。その以外の値を入力する場合、 初期摩擦角のデフォルト値を30に初期化して自動的に入力されます。
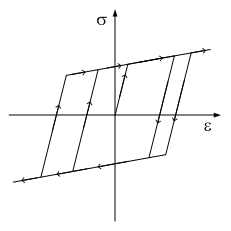
硬化則
材料が降伏する時に塑性変形による降伏面の変化を定義します。
降伏面の変化の形によって、硬化則は次のような3種で分類できます。
等方硬化則:等方性の硬化モデル
移動硬化則:移動型の硬化モデル
混合硬化則:混合型の硬化モデル
Note4
上の3つ硬化法則に対する詳しい内容は"Analysis & Design″マニュアル非線形解析の硬化法則の部分を参照してください。
Back Stress 係数:等方硬化則の程度表示
等方硬化則の場合 : '1'
移動硬化則の場合 : '0'
混合硬化則の場合 : '0 ~ 1'の間の値
Note5
塑性ひずみのすべての増分は次のように等方硬化と移動硬化に対する成分で分けて表示することができます。
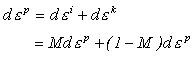
ここでMはBack Stress係数で'0~1'の値を持ちます。
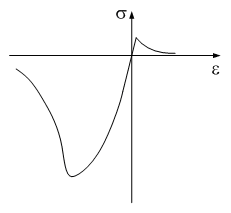
硬化係数:降伏以後の材料の接線剛性を入力します。
一般的に1次降伏以後には初期接線斜めより小さくなるとか一定の値を持つようになります。
Note6
塑性材料(Von Misesである場合)の硬化係数は材料のElastic
Modulus以上の値を入力することができません。
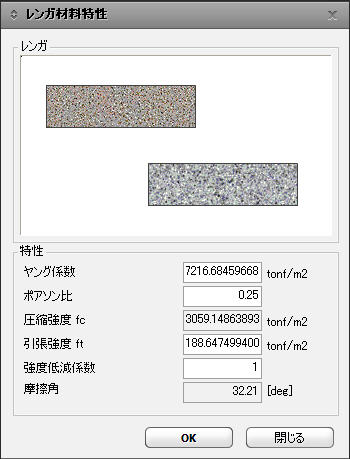
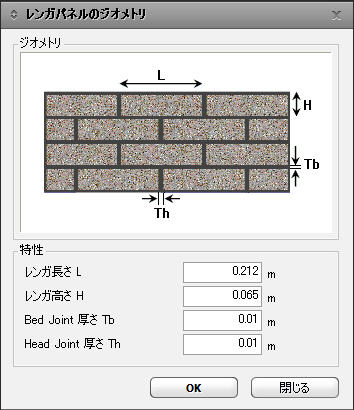
組積が選択された場合
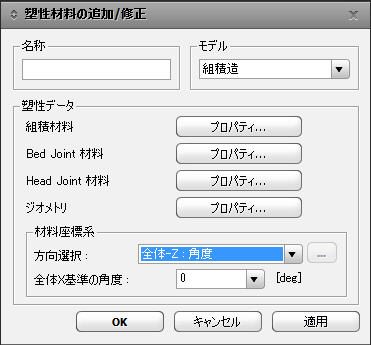
材料座標系
方向選択:組積造は直交違方性材料ですので、材料座標系の定義が重要です。
(組積造の垂直軸:組積造の水平軸で示しています。)
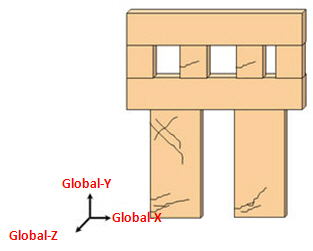
全体-Y:全体-X
全体Yと全体Xは、重力方向と組積造の水平方向と一致いなければなりません。
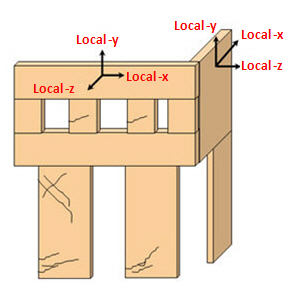
要素-y:要素-x
要素yと要素xは、重力方向と組積造の水平方向と一致いなければなりません。
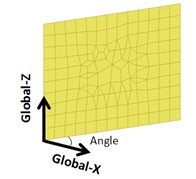
全体-Z:角度
全体Zと指定した角度は、重力方向と組積造の水平方向と一致いなければなりません。
Note8
組積材料モデルは等価の直交異方性モデルですので、材料軸方向を適切に設定しなければなりません。
ですので、全体Y:全体Xより、要素yと要素xや全体Z:角度で材料座標系を指定したほうが良いです。