Integral Bridge Spring Supports

 

▒ 기능

Integral Bridge는 상부구조에 신축이음장치를 두지 않고, 상부구조와 교대를 일체화 시킨 교량 형식으로서 상부구조의 변형을 교대와 말뚝의유연한 거동으로 흡수하도록 합니다.

이러한 형식에서는 온도변화로 인한 상부구조의 변형이 주된 관심사이며, 상부구조의 팽창/수축으로 인해 교대 배면의 지반이 영향을 받게 됩니다. 상부구조의 팽창으로 인한 토사의 압축과 상부구조의 수축으로 인한 배면 토사의 흘러내림이 반복되면서 교대 배면은 깊이에 따른 지반반력계수와 토압분포가 달라지게 됩니다.

상부구조가 팽창했다가 다시 수축하는 것을 한 주기(Cycle)라고 했을 때, 이 주기가 무한히 반복되면 배면지반의 지반반력계수 분포가 일정한 특성으로 수렴한다고 제안한 Lahane의 실험식을 사용하여 지반스프링을 할당합니다.

이러한 특성을 반영하기 위해 수평반향은 압축전담스프링으로, 접선방향은 선형탄성스프링으로 지반을 모델링합니다.

 

▒ 호출

메인 메뉴에서 [Boundary] 탭 > [Spring Supports] 그룹 > [integral Bridge]

 

▒ 입력

■ Abutment Spring

교대배면과 기초의 지반스프링을 자동 배치합니다. 교대 배면은 압축전담스프링()으로, 교대 기초는 선형 탄성스프링()으로 정의합니다.

입력된 데이터는 Point Spring Supports Table 에서 확인할 수 있습니다.

Elements of Abutment

Direction : Elastic Link의 배치방향을 선택합니다.

Element List : 교대 배면의 지반스프링을 입력할 요소선택

-보요소에 스프링을 설치할 경우에 사용할 수 있는 단면은 Solid Ractangle(), Box() 두가지로 제한됩니다.

-Beta Angle이 입력된 보요소 교대의 종방향 길이는 투영길이()로 계산되며, 이 길이는 Footing의 종방향 길이에도 적용됩니다.

 

Select Nodes for Footing

-기초부의 지반스프링을 연결할 절점을 선택합니다.

-기초부에 해당하는 절점은 일직선상에 있어야 합니다.

-일직선상에 있는 절점이라도 요소가 연속되지 않으면, 연속된(2개 이상) 절점만 선택하여 지반스프링을 입력합니다.

-Solid요소로 모델링한 경우에는 교대/기초 폭의 중앙부에 절점이 생성되도록 해야 하며, 아래 그림에서 파란색으로 표시한 부분의 절점을 선택합니다.

 

Geometry Data

Abutment Height (H) : 교대 높이

Abutment Width (B) : 교대 너비

Deck Length (L) : 바닥판의 종방향 길이

 

Soil Parameter

Void Ratio (e) : 교대 배면 흙의 간극비

Specific Gravity (Gs) : 교대 배면 흙의 비중, 일반적으로 2.65를 사용합니다.

Cycle factor (fcyc) : [Cosgrove et al (2001)]과 cycle에 따른 공극률의 감소로 2의 값으로 정의합니다. 온도하중에 의해 상부구조가 팽창/수축되고, 일체화된 교대도 함께 변형하게 됩니다. 이 Cycle이 무한히 반복될 때의 상태를 경험식으로 표현할 때, 사용되는 상수입니다.

 

Thermal Extension

Differential Deck Temp. : 바닥판의 온도증가량

α : 바닥판의 열팽창계수

 

Strip Footing Spring Data

Found. Width (W) : 기초폭

Found. Bearing Pressure (p') : 기초 지지력

Rotation Direction : 기초의 회전방향. 기초의 길이방향이 y라면 Ry를 선택합니다.

 

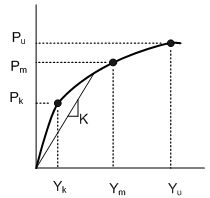
교대배면 압축전담스프링의 강성계산

단위면적당 강성
Broms(1971)에 따르면 Integral Bridge의 기초 배면 지반의 횡방향 변위와 횡방향 응력은 위의 그림과 같은 관계를 갖고 있으며, 단위면적당 강성은 다음과 같이 계산합니다.

 

Spring의 강성
최종적인 Spring 강성은 이 단위면적당 강성에 면적을 곱하여 계산됩니다.

 

교대기초 선형 탄성스프링의 강성계산

단위면적당 강성

 

Spring의 강성
최종적인 Spring 강성은 이 단위면적당 강성에 면적을 곱하여 계산됩니다.

 

■ Pile Spring

말뚝의 지반스프링을 자동 입력합니다. 말뚝의 횡방향은 대칭 비선형 탄성스프링()으로, 말뚝의 접선 방향은 선형 탄성스프링()으로 정의합니다.

강성이 계산된 지반스프링은 General Type의 Point Spring Supports로 입력되며, 입력된 데이터는 Point Spring Supports Table 에서 확인할 수 있습니다.

Pile Spring Data

Soil Type : Sand / Soft Cray / Stiff Cray의 세가지로 구분할 수 있으며, 선택하는 토사의 종류에 따라 강성계산 방법이 달라집니다. 아래의 스프링강성 계산방법을 참조하시기 바랍니다.

Ground Level : 지표면의 Z좌표

Pile Diameter(D) : 말뚝의 지름

Unit Weight of Soil(γ) : 흙의 단위중량

Earth Pressure Coeff. at rest(K0) : 정지토압계수

Coeff. of Subgrade Reaction(Kh) : 지반반력계수

Internal Friction Angle (Φ) : 흙의 내부마찰각

Initial Soil Modulus(k1) : 상대밀도에 따라 결정되는 상수로 말뚝의 수평방향 비선형 탄성스프링의 강성결정에 사용됩니다. 아래의 k점과 m점의 정의 부분을 참조하시기 바랍니다.

 

말뚝 (수평방향) 비선형 탄성스프링의 강성계산

임의 깊이 X에서 횡변위 Y와 단위길이당 지반반력(kN/m)의 관계는 왼쪽의  그래프와 같은 관계를 가집니다.

임의 깊이 X(즉, 지반스프링의 위치)에서 Pk, Pm, Pu, Yk, Ym, Yu의 값이 정의됩니다.

지반의 종류에 따라 Pu를 정의하는 계산방법이 달라지며, Pk, Pm, Yk, Ym, Yu 의 위치는 Pu를 통해 동일한 방법으로 계산됩니다.

계산방법은 크게 Sand와 Clay로 분류되며, J값을 다르게 적용하여 Soft Clay와 Stiff Clay로 구분합니다.

지반이 사질토(Sand)인 경우의 Pu
Xt 값은 아래 두가지 경우의 Pu가 같을 경우에 대한 깊이 값을 나타내므로 Pu에 대한 아래 두 식을 같게 놓고 X에 대하여 정리하여 2차방정식을 풀어 해를 구한 후 적절한 값을 선택합니다.

 

지반이 점토(Clay)인 경우의 Pu

 

k점과 m점의 정의

 

Spring의 강성
최종적인 Spring 강성은 앞에서 계산한 단위면적당 강성에 면적을 곱하여 계산됩니다.  

 

말뚝 (접선방향) 선형 탄성스프링의 강성계산

말뚝 접선방향 선형 탄성스프링의 방향은 지면에 수직인 방향(전체좌표계 -Z) 이며, Pile이 지면에 수직이 아닌 경우에는 Pile을 구성하는 절점의 절점좌표계 z방향이 전체좌표계 Z방향과 일치하도록 절점좌표계(Node Local Axis)를 수정해야 합니다.