점 스프링

선선택된 절점에 일정한 강성을 갖는 스프링을 생성합니다. 전체좌표계 기준으로 변형 및 회전에 대한 구속을 스프링상수 혹은 감쇠상수를 이용하여 정의합니다. 주로 지반에 의한 탄성지지조건 혹은 동해석의 구속조건으로 사용됩니다.

매트릭스 스프링

점 스프링 기능과 동일합니다. 단, 특성정의 시 변형 및 회전에 대한 스프링 상수를 매트릭스(행렬)를 통해 직접 입력할 수 있습니다.

강체링크

선택된 두 절점을 연결하는 링크요소를 생성합니다. 기준이 되는 첫 번째 절점을 선택하고 연결대상이 되는 여러 개의 절점을 한번에 선택할 수 있습니다. 강체링크는 두 절점 사이 변형 혹은 회전에 대한 일체거동을 모사하기 위해 사용되며, 전체좌표계 기준으로 구속 방향을 정의할 수 있습니다.

탄성링크

선택된 두 절점을 일정한 강성을 갖는 스프링으로 연결합니다. 기준이 되는 첫 번째 절점을 선택하고 연결대상이 되는 하나의 절점을 선택하여 생성합니다. 점 스프링과 같이 변형과 회전에 대한 일정강성으로 특성을 정의합니다.

보간요소

선택한 절점들의 거동의 평균에 가중치를 적용하여 이를 기준(참조)절점의 거동으로 모사하기 위해 생성합니다. 강체링크 요소와 마찬가지로 연결된 절점들 간의 운동을 구속하는 역할을 하지만, 강체링크와는 달리 하나의 절점이 다른 여러 절점의 운동에 따라 상대적인 거동을 할 수 있도록 생성하는 요소입니다. 즉, 선택한 여러 주 절점들의 평균적인 거동이 참조절점(종속절점)의 움직임을 결정하는 형태가 됩니다.

구속하고자 하는 절점과 자유도를 선택한 후, 평균을 취하고자 하는 절점들을 선택합니다. 각 절점별로 가중치를 적용할 수 있습니다.

<강체링크>                                  <보간요소>

면 스프링

요소의 지지점에 단위면적당 스프링강성을 입력하여 점스프링 또는 탄성링크를 생성합니다.

기초나 지하구조물의 해석 시 지반에 의한 탄성지지조건을 고려할 때 사용됩니다. 단위면적당 스프링상수를 입력하면 선택된 요소면적을 고려하여 절점에 작용되는 스프링 또는 링크로 자동 환산 됩니다.

면 스프링 입력대상은 아래와 같습니다.

• Frame : 1D 요소의 절점에 점스프링 또는 탄성링크를 생성합니다. 보요소의 단위길이당 지지강성을 계산하기 위한 폭을 너비에 입력합니다.

• Planar : 2D 요소를 선택하여 스프링 또는 링크를 생성합니다.

• Solid-Face : 3차원 Solid의 임의 면을 지정할 수 있으며, 선택한 면에 연결된 모든 절점에 스프링 또는 링크를 생성합니다.

• Element Edge : 2D 요소의 경계선을 선택하여, 선택된 경계선에 연결된 절점에 스프링 또는 링크를 생성합니다.

단위면적당 입력되는 탄성링크는 스프링상수를 정의하는 방식 이외에 별도로 "인장전담", "압축전담" 옵션을 적용할 수 있습니다.

지반 면 스프링

Demo영상 다운받기

 - 점성/탄성경계 자동생성

동해석에 필요한 탄성/점성 경계요소를 자동으로 생성하는 기능입니다. 자동경계요소를 생성할 요소망을 선택하면 선택된 요소망의 좌/우/바닥부에 자동으로 경계요소가 생성되며, 요소에 할당되어 있는 재료/특성에 따라 스프링 상수 값이 자동계산 됩니다.

동해석 수행 시 모델 하부(바닥면)의 경우 기반암 조건을 모사하기 위해 고정조건(변위구속)을 사용하는 것이 일반적입니다. "바닥 고정조건" 체크옵션을 통해 간단히 설정할 수 있습니다.

탄성경계요소 생성방법

• 고유치해석, 응답스펙트럼해석을 수행하기 위해서는 지반의 경계조건으로 탄성스프링을 활용합니다.

• 이러한 탄성스프링을 생성하는 방법은 초급 해석자에게는 어려운 일이며, 다음과 같은 절차를 통해 탄성스프링요소를 생성합니다.

1. 지반의 입력물성 가운데 탄성계수를 통해 Kv0를 산정합니다. (산정식은 다음과 같습니다.)

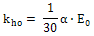
여기서, E0 : 지반의 탄성계수, a : 실험조건에 따른 계수 (표 참고)

2. 산정된 Kv0를 통해 지반반력계수 Kv(= Kh)를 재계산합니다.

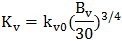
여기서,  

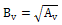
이 때 면적 Av는 지반반력 스프링이 설치될 구역의 면적이 됩니다.

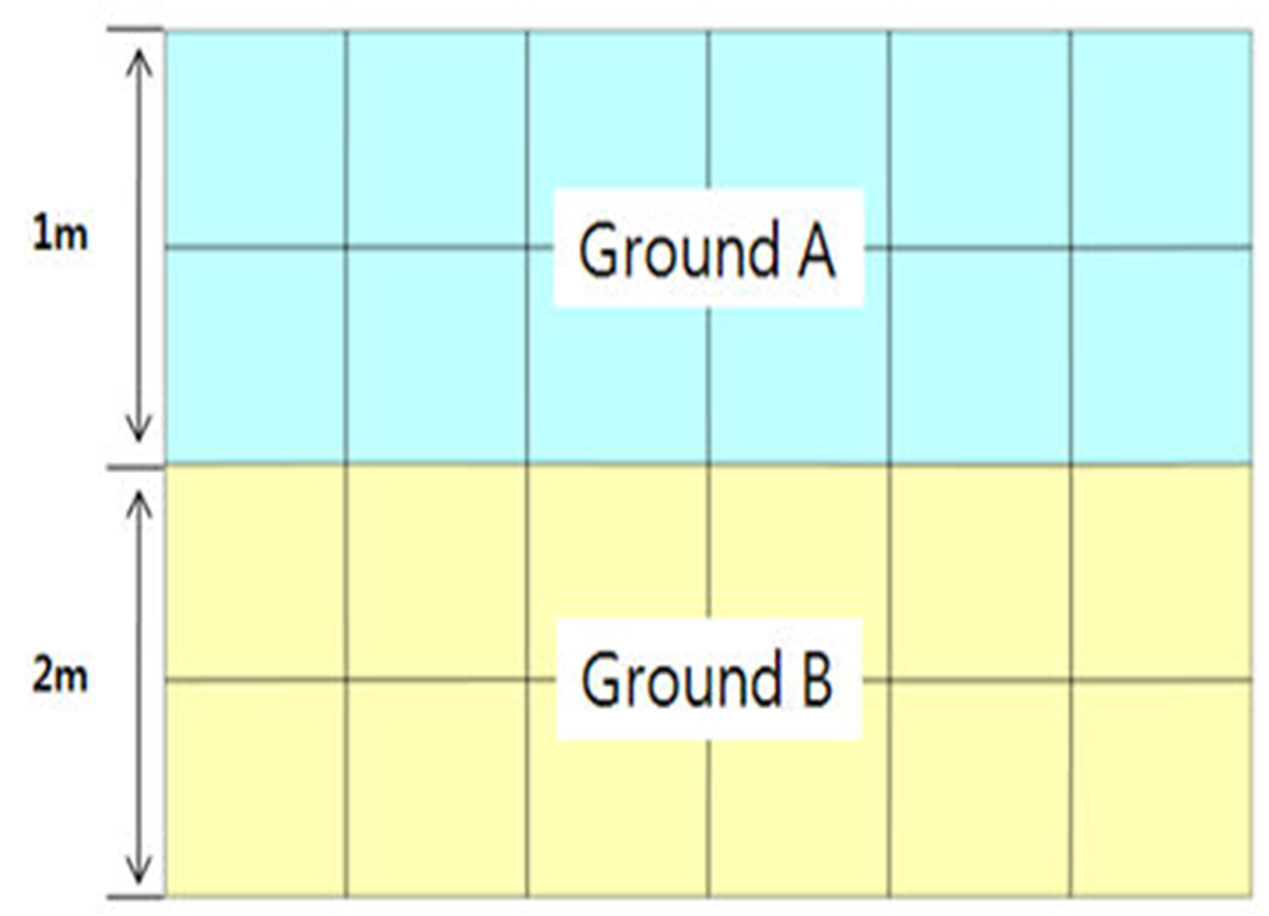
*아래 그림과 같은 모델이 있는 경우

Ground A의 면적 Av=1m(모델왼편의 길이)*1m(2D해석 시 단위폭)=1m2, Bv는 1m=100cm가 됩니다.

같은 방법으로 Ground B의 유효폭 Bv=√(20000)cm=141.42136 cm이 됩니다.

최종적으로 아래와 같이 지반반력계수 K값을 산정하여, 요소의 면적이 고려된 점 스프링이 절점에 생성됩니다.

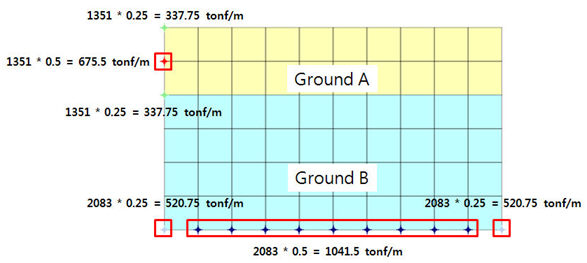
바닥부(Z방향)의 스프링계수는 X방향과 동일한 값으로 생성됩니다.

(요소의 길이 x 폭(1m)=단면적이므로 요소의 유효길이만 고려합니다.)

지반과 지반이 만나는 부분에서는 중복된 2 개의 경계요소가 생성됩니다.

점성경계요소 생성방법

• 시간이력해석을 수행하기 위해서는 모델의 경계조건으로 점성경계요소가 필요합니다.

• 점성경계요소를 생성하는 방법은 다음과 같습니다.

1. Cp, Cs의 산정

Cp, Cs는 아래의 식을 통해 계산됩니다.

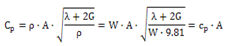
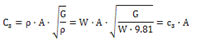
여기서, , ,

λ : 체적탄성계수, G : 전단탄성계수, E : 탄성계수, ν : 포아송비, A : 단면적

2. 단면적의 경우 surface spring이 생성될 때 자동적으로 고려되므로 Cp, Cs만을 산정합니다.

tonf•sec/m3 단위인 Cp, Cs에 단면적이 곱해져 최종적인 점성경계요소의 스프링 강성은 tonf•sec/m가 됩니다.

음영으로 표시된 셀의 parameter는 사용자가 모델링 시 입력하는 지반의 물성이며, 체적탄성계수와 전단탄성계수는 탄성계수+포아송비를 통해 계산합니다. 따라서 사용자가 점성경계요소를 생성하는 경우 추가적으로 입력할 사항은 없습니다.

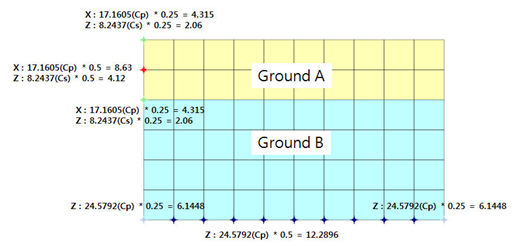
점성경계요소를 자동으로 생성하는 경우 아래와 같이 요소의 면적(유효길이*단위폭)을 고려하여 자동으로 스프링이 생성됩니다. 스프링이 생성되는 절점에 수직한 방향의 계수에 Cp를 입력하고 평행한 방향에 Cs의 값이 입력됩니다.

예를 들어, 모델의 좌/우측에 생성되는 스프링 계수의 Cx는 각 지반의 Cp값이며, Cz는 Cs값이 됩니다.

바닥부는 스프링계수 Cz가 Cp값이 됩니다.

게이징 쉘

솔리드요소로 만들어진 구조물에서 솔리드 요소 표면의 힘과 모멘트를 확인할 수 있도록 쉘 요소를 생성합니다. 게이징 쉘을 생성하기 위해 기반이 되는 솔리드 요소를 선택한 후, 선택된 솔리드 요소에서 게이징 쉘을 추출하기 위한 요소면을 선택합니다. 게이징 쉘의 강성은 선택된 솔리드 요소 강성에 강성 증분 계수를 적용하여 계산되며, 두께는 선택된 솔리드 형상의 두께를 자동 고려하여 각 요소별 두께를 계산됩니다.

<요소면 선택>

<가우징요소 두께(빨간점선길이)>

질량

임의 절점에 집중질량을 입력합니다. 하중을 질량으로 환산하여 해석에 적용할 때 생성하는 요소입니다.

질량특성에서 입력한 집중질량 데이터를 선택한 절점에 자동으로 분할 입력하고자 할 경우 전체질량에 체크합니다. 전체질량 기능을 사용하여 절점에 분할 입력된 집중질량 데이터의 총합은 질량특성에서 입력한 집중질량 데이터와 같습니다. 하중의 총합을 질량으로 치환한 값을 입력한 후 전체질량 옵션을 선택함으로써 고유치 해석, 응답스펙트럼해석, 시간이력해석 등을 위한 질량 데이터를 편리하게 적용할 수 있습니다.

집중질량데이터는 전체좌표계 기준으로 입력하며, 질량관성모멘트(I) 는 정해진 단위계에 따라 정의합니다.