힌지
속성 생성/수정
부재의 비탄성 영역의 분포 여부 및 해석방법에
따라서 집중형과 분포형으로 구분됩니다.
보
- 집중형 : 소성변형이 가능한 길이가 없는 병진 또는 회전 비탄성 스프링을
보요소에 삽입하여 모델링되고 비탄성 스프링을 제외한 나머지 부분은 탄성으로 모델링
됩니다. 축변형에 대해서는 부재 중앙, 휨과 전단성분에 대해서는 부재 양 단부에 위치합니다.
따라서 축방향 변형의 경우에는 힘-변위의 관계로, 휨변형의 경우에는 단부에서의 모멘트-회전각
관계로 정의됩니다.
보
- 분산형 : 집중형 힌지 형태와는 달리 부재의 전 구간에 대하여 비탄성
거동이 발생한다고 가정합니다. 사용자에 의하여 지정된 부재 길이방향의 소성힌지 위치가
적분점으로 정의되고 부재의 내력분포를 나타내는 단면의 유연도 행렬은 Gauss-Lobatto
수치 적분법을 통하여 계산됩니다. 적분점의 수는 비탄성 스프링의 개수를 제외하고 1개에서
최대 8개까지 설정 가능합니다. 적분점이 2개인 경우는 Classical Gauss
integration을 사용합니다.
트러스 : 부재 축방향 성분에 대해서 부재
중앙(center)에 힘-변위관계로 정의되는 스프링을 배치하고, 스프링의 비탄성 이력거동은
골격곡선(skeleton curve) 모델로 정의합니다.
점
스프링/탄성 링크 : 재료 및 부재의 비탄성 특성에 영향을 받는 집중형(Lumped),
분산형(Distributed 힌지와는 달리 스프링(Spring)/탄성링크(Elastic
Link Hinge)는 각 성분별 탄성 특성에 대해 비탄성 소성힌지 속성을 정의할
수 있습니다. 각 성분의 탄성강성은 유효강성에 의하여 정의되며 비탄성 해석에서는 초기강성의
역할을 합니다. 비탄성 이력거동은 골격곡선(skeleton curve) 모델로 정의하고,
3개의 병진방향과 3개의 회전방향에 대하여 모두 비탄성 특성을 정의할 수 있습니다.
종류는 직교와 원통좌표계가 있습니다. 세
점을 입력하여 좌표계의 세 평면 12, 23, 31 (XY, YZ, ZX) 중 한
평면을 정의하는 방법으로 좌표계를 설정합니다. 즉, 입력한 세 점을 지나는 평면이
설정한 12, 23, 31 평면중 하나가 되고, 다른 두 평면은 설정된 평면의 방향에
의해 자동으로 결정됩니다.
평면을 선택하고, 원점과 설정한 평면 1축상의 점, 설정한 평면상의 점을 차례데로 설정하여
기준평면의 위치와 방향을 결정합니다.
상관타입
축력과 모멘트 사이의 상관작용을 고려하는
방식을 선택합니다. Single Component 는 방향 별 각 성분의 특성이 독립적으로
거동한다고 가정하는 일축힌지 이력모델로 정의됩니다. Multi Component는
다축힌지 이력모델을 정의하는데 사용되고 모멘트-곡률 관계를 매우 정확하게 추적할 수
있습니다.
없음
: 축력과 모멘트의 상관작용을 고려하지 않는 경우입니다.
P-M
: P-M 상관작용은 축력의 영향을 고려하여 힌지의 휨항복강도를 산정하여 반영할 수
있습니다. 이 방식에서는 2축 휨모멘트의 상관작용은 무시되며 각각의 시간증분(time
step)에 대한 힌지의 상태판정을 할 때는 축력과 2개의 휨 모멘트는 모두 상호
독립적인 것으로 가정합니다.
축력을 고려한 휨 모멘트 항복강도의 재산정은 다음 조건을 만족하는 하중조건에서 수행합니다.
1) 연속적으로 해석되는
일련의 시간이력 하중조건 가운데 첫 번째
2) 비선형 정적해석을 수행
P-M-M
: 이 방식은 다축힌지 이력모델을 사용함으로써 비탄성 해석에 반영할 수 있습니다.
축력 및 2축 휨 모멘트 사이의 상호작용을 소성이론을 응용하여 구현합니다. 각각의
시간증분마다 3개 성분의 변동을 통합적으로 고려한 상태판정을 수행하며, GTSNX에서는
이동경화형 (kinematic hardening type)이 지원됩니다.
항복면
파라미터
P-M, P-M-M 일 때 항복면 함수를
정의합니다. 속성에 여러 개 함수를 할당할 수 있습니다. P-M 상관곡선의 형상을
입력합니다. 상관곡선의 형상은 곡선상의 정규화된 좌표로 표현됩니다. 정규화된 좌표의
축력 성분을 계산 또는 도시함에 있어서 압축인 경우에는 (-), 인장인 경우에는 (+)로
약속합니다.
컴포넌트
단면내력의 각 성분 별로 입력되는 비탄성
힌지의 속성입니다. Beam, Point Spring, Elastic Link 타입에서는
모든 방향 성분이 입력 가능하며, Truss 타입에서는 Tx, Rx 성분만 가능합니다.
힌지위치
: Lumped 힌지의 위치를 선택합니다. 축력성분은 부재 중앙에 고정되며 전단 및
휨모멘트 성분에 대해서는 요소의 I단, J단 또는 양단(I&J)을 선택할 수
있습니다.
적분점개수
: Distributed 힌지에 대하여 적분점의 개수를 입력합니다. 8개까지 입력이
가능하며 입력된 수에 따라 각 단면에서의 힘-변위 또는 변형의 관계가 계산됩니다.
이력모델
: 비탄성 힌지에 대한 이력모델을 선택합니다.
힌지
컴포턴트
비탄성 힌지 이력모델을 정의합니다. Multi
Component는 Beam 타입에만 할당 가능합니다.
-
Origin-oriented : 초기 재하시의 응답점은 골격곡선 상에서
이동합니다. 제 1차 항복 이후에 제하되는 경우 원점을 지향하는 직선상을 이동합니다.
제하 과정에서 재재하 되는 경우는 제하 시와 같은 기울기의 직선상을 이동하고 골격곡선과
만나면 골격곡선상에서 이동합니다.
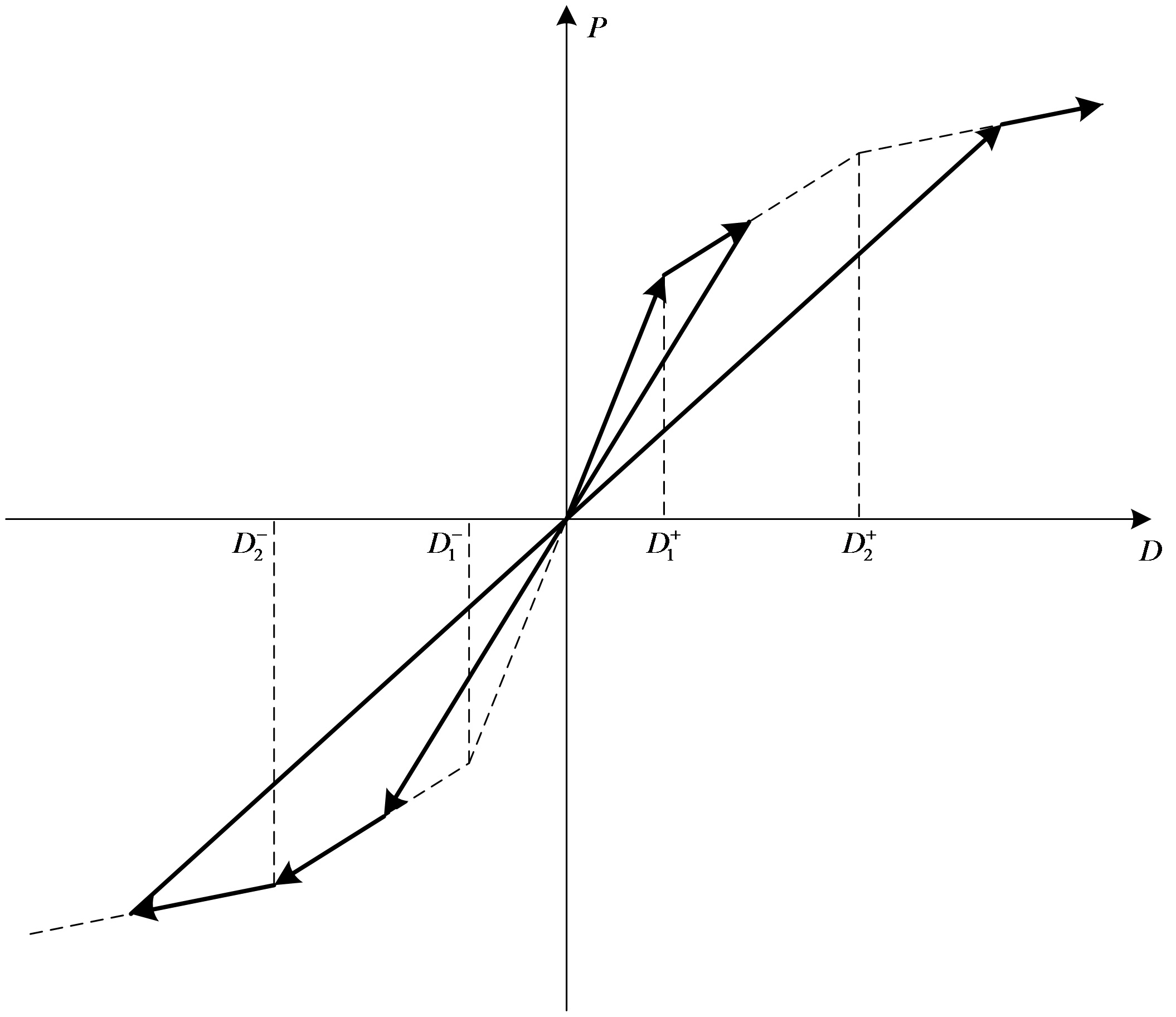
-
Peck-oriented : 초기 재하시의 응답점은 골격곡선 상에서 이동합니다.
제 1차 항복 이후에 제하되는 경우 반대측의 최대 변형점을 지향하는 직선상을 이동한다.
만약 반대측이 1차 항복점을 지나지 않은 경우는 1차 항복점이 최대 변형점이 됩니다.
제하과정에서 재재하되는 경우는 제하시와 같은 기울기의 직선상으로 이동하고 골격곡선과
만나면 골격곡선상에서 이동합니다.
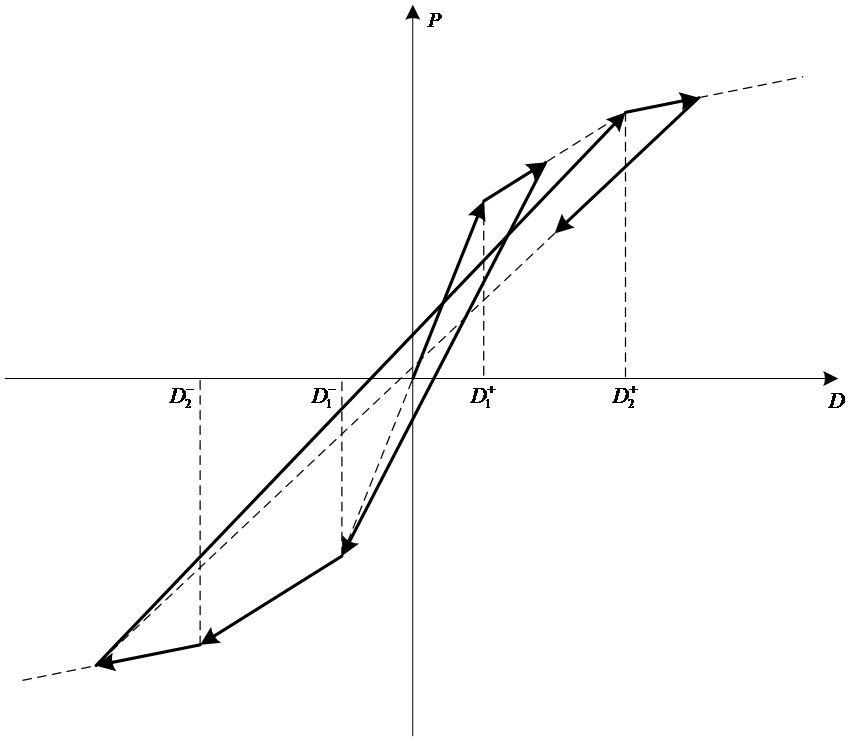
-
Kinematic : 초기 재하시의 응답점은 3선형 골격곡선상에서 이동합니다.
제하 강성은 탄성강성과 동일하며, 항복 후 강성은 정(+), 부(-) 대칭 정의만
가능합니다. Kinematic 모델의 경우 축력과 2축 휨성분을 소성이론에 의해 상호작용을
고려할 수 있습니다.
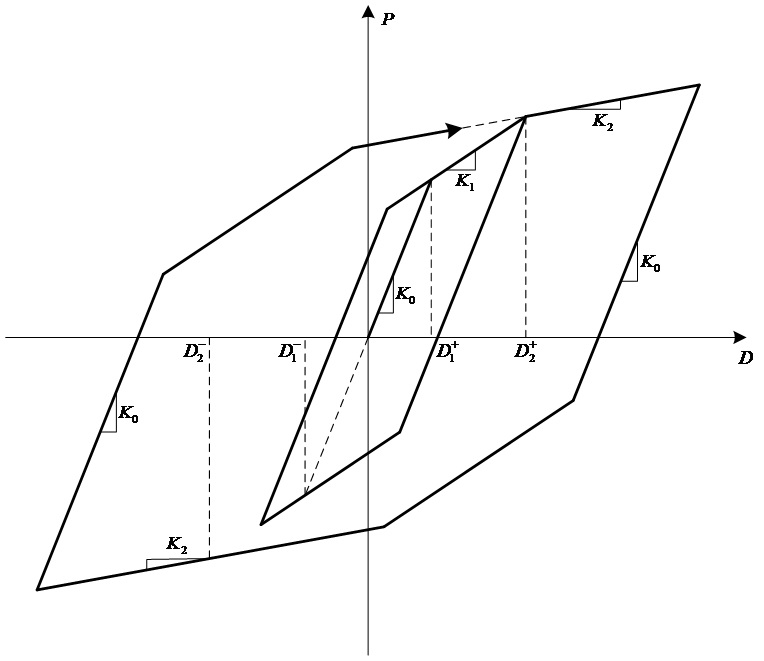
-
Clough : 초기 재하시의 응답점은 골격곡선 상에서 이동하며 항복
후에는 변형의 진전에 의해 재하 강성이 점진적으로 감소하는 형태입니다. 콘크리트는
건조수축 등에 의해 균열이 발생하기 쉬우므로 균열전의 상태는 무시하고 전체 단면에
균열이 발생한 것으로 간주하여 인장철근의 휨항복에 의한 강성변화만을 고려하도록 고안된
모델입니다.
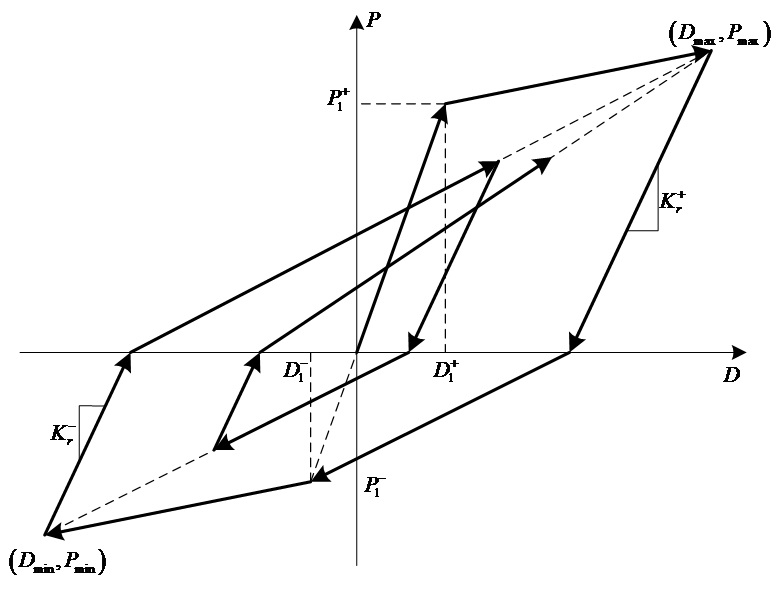
-
Degrading : 초기 재하시의 응답점은 골격곡선 상에서 이동하며
1차 항복후, 2차 항복 이전에는 Bilinear로 거동하고 2차 항복 이후는 변형의
진전에 의해 제하강성이 점진적으로 감소하는 모델입니다.
-
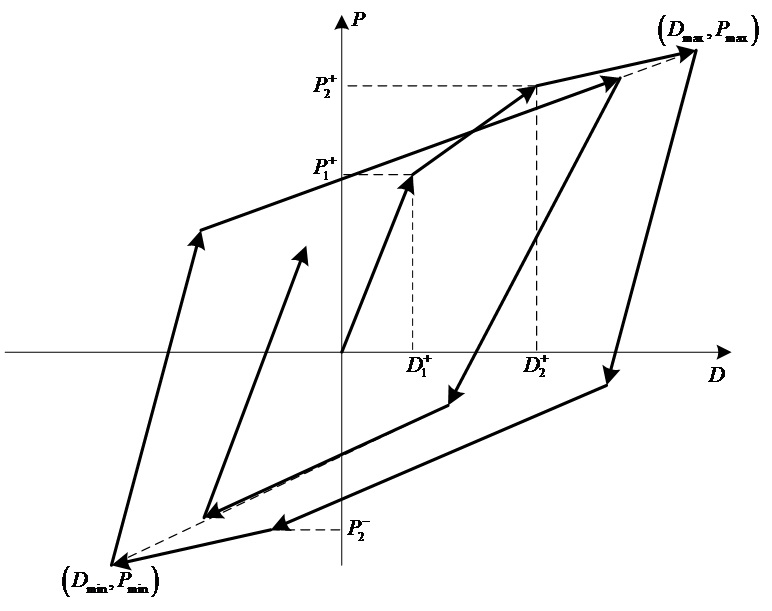
Takeda : 철근 콘크리트 부재의 실험에 의해 관찰된 복원력특성을
나타낸 모델입니다. 제하점의 골격곡선상에서의 위치 및 반대편 영역에서의 1차 항복여부에
의해 제하강성이 결정됩니다.
-
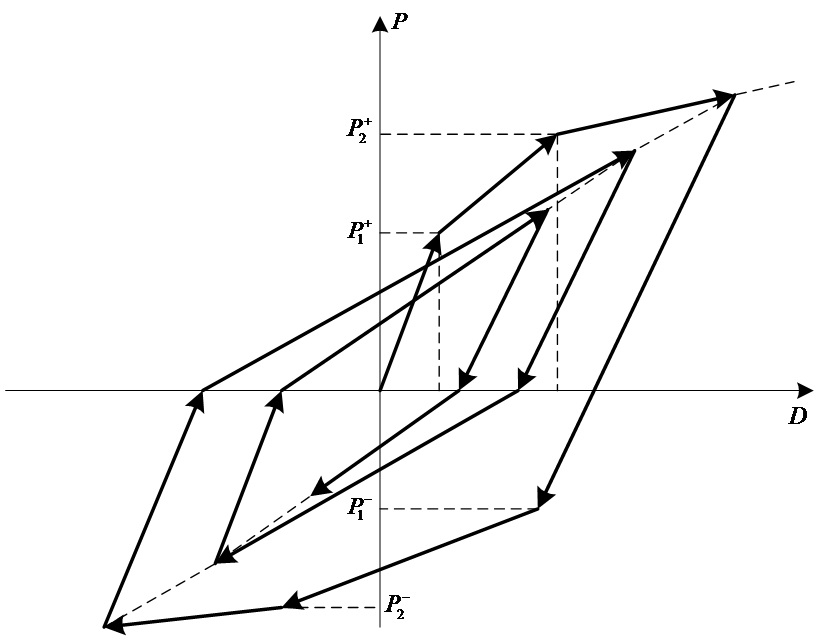
Modified Takeda : 초기재하 시의 응답점은 3선형 골격곡선상에서
이동합니다. 현재의 변위 혹은 변형, D가 처음으로 D1±을 넘은 경우, 혹은 현재까지의
최대 변형점을 넘은 경우는 3선형의 골격곡선 상에서 이동합니다. 이 직선으로부터 제하(Unloading)되어
반대방향으로 향하는 경우, 복원력이 0이 되는 점까지는 제하직선을 따라 이동하여,
복원력이 0인 점을 넘은 후에는 반대측의 최대 변형점을 향합니다.

-
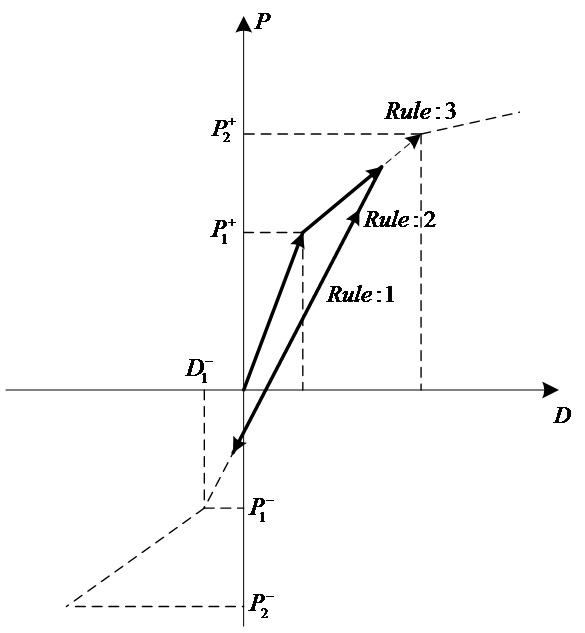
Normal Bilinear : 초기재하 시의 응답점은 2선형 뼈대곡선(Skeleton
Curve)상에서 이동합니다. 제하(unloading)강성은 탄성강성과 동일합니다.
-
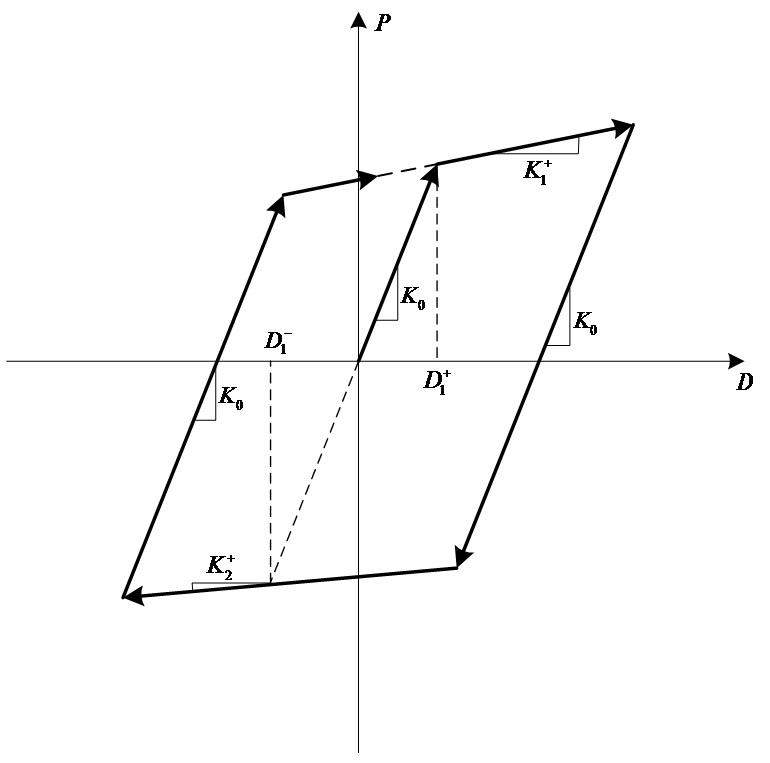
Modified Ramberg-Osgood : Ramberg-Osgood
모델은 원래 금속재료의 동역학 모델로 제안된 것이지만 타츠오카에 의한 수정된 모델입니다.

Maximum Damping : 등가점성감쇠(이력감쇠) 정수 h는 다음 식으로
정의됩니다.
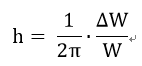
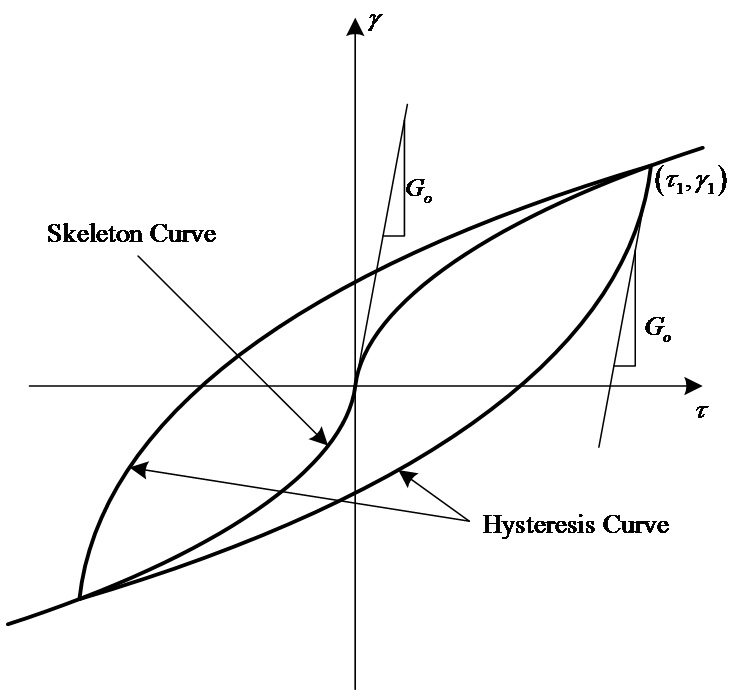
최대 감쇠정수 hmax의 값에 관해서 h-γ
곡선에 있어서 근사적으로 h가 거의 일정치로 수렴하는 대변형 레벨에서의 h 값을 사용하는
것이 일반적입니다. 기준변형율(reference strain)로서 흙의 전단강도 τ와
Go를 사용하여 γ_r= τ/Go 가 됩니다.
-
Modified Hardin-Drnevich : 골격곡선만 제안되어 있는
Hardin-Drnevich 모델에 코쿠쇼가 Massing 법칙을 적용시켜 이력곡선을
정의 한 모델입니다.

- Multi
Kinematic
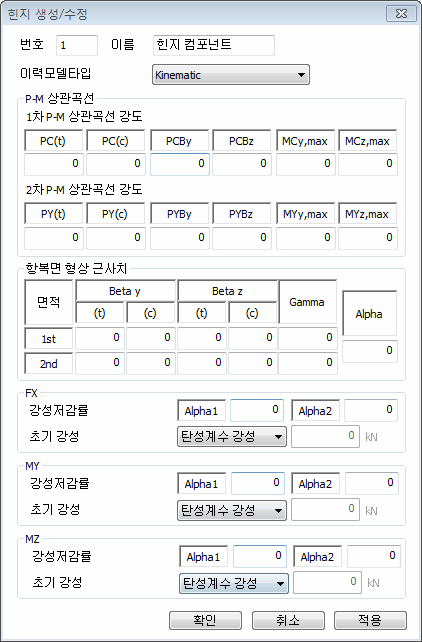
P-M
상관도: 3차원 항복면 상정에 필요한 P-M 상관곡선의
데이터를 입력합니다. |
|
1차 P-M 상관곡선
강도 : 1차 항복 상관곡선에서의 강도
PC(t) : 순수 인장력에
대한 1차항복강도.
PC(c) : 순수 압축력에
대한 1차항복강도.
PCBy : 단면의 y축-휨에
대한 1차항복 상관곡선에서 균형파괴 발생시의 축력
PCBz : 단면의 z축-휨에
대한 1차항복 상관곡선에서 균형파괴 발생시의 축력
MCy,max : 단면의 y축-휨에
대한 1차항복 상관곡선에서 최대 휨 항복강도
MCz,max : 단면의 z축-휨에
대한 1차항복 상관곡선에서 최대 휨 항복강도
2차
P-M 상관곡선 강도 : 2차 항복 상관곡선에서의 강도
PY(t) : 순수 인장력에
대한 2차항복강도.
PY(c) : 순수 압축력에
대한 2차항복강도.
PYBy : 단면의 y축-휨에
대한 2차항복 상관곡선에서 균형파괴 발생시의 축력
PYBz : 단면의 z축-휨에
대한 2차항복 상관곡선에서 균형파괴 발생시의 축력
MYy,max : 단면의 y축-휨에
대한 2차항복 상관곡선에서 최대 휨 항복강도
MYz,max : 단면의 z축-휨에
대한 2차항복 상관곡선에서 최대 휨 항복강도 |
항목면
형상 근사치 : P-M 상관곡선을 기초로 3차원 항복면의
파라미터를 사용자 입력합니다.
각각의 파라미터는 아래 항복곡면의 식에서 사용되는 값입니다. |
|
PY(t)
: 순수 인장력에 대한 2차항복강도.
PY(c) : 순수 압축력에
대한 2차항복강도.
PYBy : 단면의 y축-휨에
대한 2차항복 상관곡선에서 균형파괴 발생시의 축력
PYBz : 단면의 z축-휨에
대한 2차항복 상관곡선에서 균형파괴 발생시의 축력
MYy,max : 단면의 y축-휨에
대한 2차항복 상관곡선에서 최대 휨 항복강도
MYz,max : 단면의 z축-휨에
대한 2차항복 상관곡선에서 최대 휨 항복강도
Beta
y, Beta z, Gamma : P-My 또는 P-Mz
상관관계의 차수로 1차 및 2차 항복에 대해 다른 값을 입력 가능합니다.
또한 Beta y, Beta z는 균형파괴 발생시 축력을 기준으로 그보다
큰 축력과 작은 축력의 영역에 대해 서로 다른 2개 값을 입력할 수
있습니다.
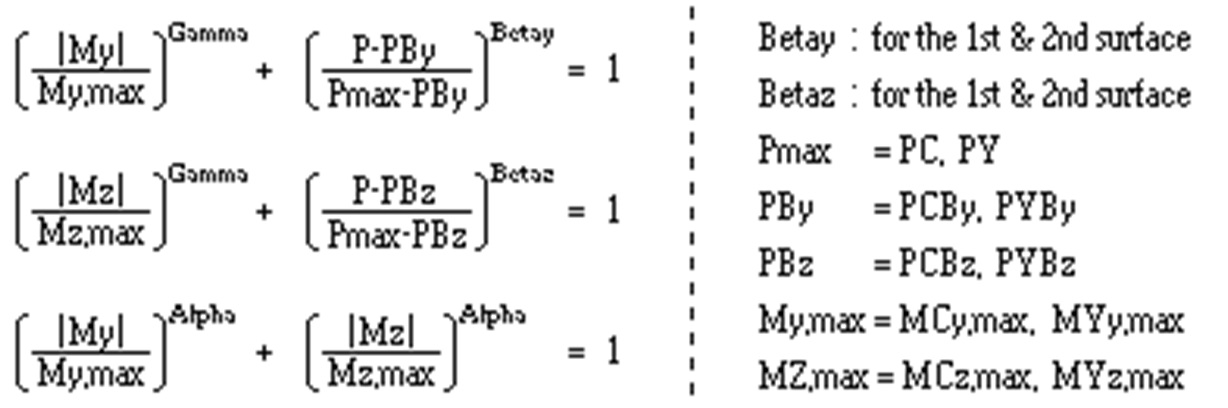
Alpha
: 1차 및 2차 항복에 대한 My-Mz 상관관계의 차수 입니다.
|
강성저감률
: 골격곡선의 강성 저감률을 입력합니다. 항복 기울기의 강성을 초기
강성으로 나눈 비를 의미합니다. Alpha1/2는 1/2차 항복 기울기의
강성을 초기 강성으로 나눈 비를 입력합니다.
초기강성
: 비탄성 해석에 사용되는 초기강성을 선택하거나 사용자가 직접 입력합니다 |
|
탄성계수 강성
: 요소에 정의된 탄성계수를 초기강성으로 사용합니다.
사용자
정의 : Stiffness Reduction 타입일 때에만
사용 가능하며, 사용자가 초기강성을 직접 입력합니다. |
|


