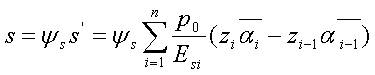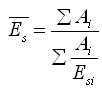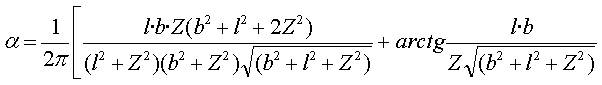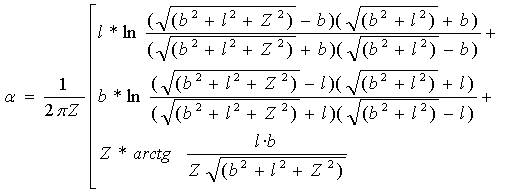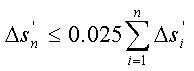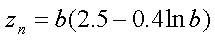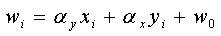17.7.1

17.7.1 一般基础沉降计算

区分

版本 / Revision No.

改善建议者

改善内容

内容列表

产品功能

Ver.112 R3 / No.2009-03

—

手册内容

Ver.110 R2 / No.2009-02

—

1	一般基础柔性假定沉降计算

功能说明

基础柔性假定适用于独基、条基、梁式基础、刚度较小或刚度不均匀的筏板基础。当选择基础柔性假定时，采用《建筑地基基础设计规范》GB50007- 2002第5.3.5条，第5.3.6条，第5.3.7条，第5.3.8条，第5.3.9条进行沉降计算。
对基础自动划分沉降计算区格，假设基础底面附加压力为直线分布，计算中考虑各区格之间的相互影响。
（1）计算公式

式中：

                 s —— 地基最终沉降量；
               s'—— 按分层总和法计算出的地基变形量；
              ψs—— 沉降计算经验系数，可参考GB50007-2002规范中表5.3.5数值；
               n —— 地基沉降计算深度范围内所划分的土层数；
             p0 —— 对应于荷载效应准永久组合时的基础底面处的附加压力；
            Esi —— 基础底面下第ｉ层土的压缩模量；
       zi,zi-1 —— 基础底面至第i层土、第i-1层土底面的距离；
      ai,ai-1 —— 基础底面计算点至第i层土、第i-1层土底面范围内平均附加应力系数，可按GB50007-2002规范中附录K采用，程序是直接采用布辛奈斯克（Boussinesq）公式计算的。

沉降计算经验ψs系数表表17.7.1-1

（MPa）基底的附加压力	2.5	4.0	7.0	15.0	20.0
p0≥fak	1.4	1.3	1.0	0.4	0.2
p0≤0.75fak	1.1	1.0	0.7	0.4	0.2

注：为变形计算深度范围内压缩模量的当量值，应按下式计算：

式中 Ai —— 第i层土附加应力系数沿土层厚度的积分值。

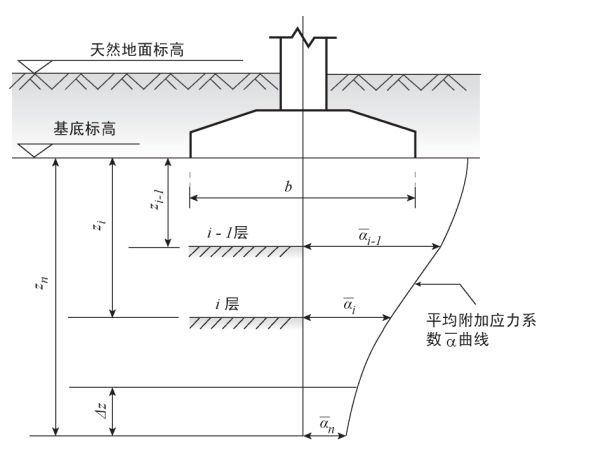
图17.7.7-1 基础沉降计算分层示意

计算平均附加应力系数 i的布辛奈克斯公式：
矩形面积上均布荷载作用下角点的附加应力系数：

② 矩形面积上均布荷载作用下角点的平均附加应力系数：

式中：

                 b —— 矩形的短边；
                l —— 矩形的长边；
               Z —— 从荷载作用平面起算的深度。

（2）沉降计算深度的确定

地基沉降的计算深度在基础大师程序中采用下列方法确定：

         ① 用户输入计算深度
      ② 按GB50007-2002规范第5.3.7条及第5.3.6条规定确定计算深度
           当采用程序自动确定计算深度时，按下列原则选择计算方法：计算独立基础的沉降且不考虑相邻荷载的影响时，采用GB50007-2002规范第5.3.7条的方法；其他情况按第5.3.6条的方法确定。
           GB50007规范第5.3.6条公式计算地基变形计算深度zn(图17.6.1)如下：

式中：

△s'i —— 在计算深度范围内，第i层土的计算变形值；
△s'n —— 在由计算深度向上取厚度为Δz的土层计算变形值，Δz见图17.6.6-1。
GB50007规范第5.3.6条公式计算地基变形计算深度zn如下：

式中：b为基础宽度。

2	一般基础刚性假定沉降计算

功能说明

基础刚性假定适用于基础和上部结构刚度较大的筏板基础，刚性基础与地基的共同作用使差异沉降得到调整，基础沉降与基础变形相互协调，刚性基础的底面在受荷前后始终保持平面，基础大师中基础刚性假定的沉降按下述方法进行计算。
计算时先将基础底面划分为n个平行于坐标轴x和y的矩形区格，由于刚性基础的底面在受荷后仍为平面，故任一矩形网格中点的位移为：

式中：

                Wi —— 矩形网格i中心点的位移；
              αy —— 基底绕y轴转动的倾斜度（即tanA，A为基础沿y轴的倾角）；
              αx —— 基底绕x轴转动的倾斜度（即tanB，B为基础沿x轴的倾角）；
        xi 、 yi —— 矩形网格i中点的坐标；
              W0—— 基底平面坐标原点位移。

根据位移协调和静力平衡，可得到如下方程：

式中：

                  fij——为修正后的地基柔度系数 fij=kijδij
                kij—— 地基模型系数，它实际上是考虑了土的应力、应变扩散能力后的折减系数；当i≠j时， kij=0.1~0.5；当i=j时，kij=1； kij取0时就称为文克尔地基模型；kij取1时就接近弹性半无限体模型，基础边缘反力过大。一般软土取小值，硬土取值大些；
                δij—— 地基区格柔度系数，即第j区格上施加单位均布压力对第i区格中点产生的沉降，沉降计算方法按第17.7.1节中的一般浅基础沉降计算；
           xi , yi —— 矩形网格i的中心坐标；
                ai —— 矩形网格i的面积；
                 qi—— 矩形网格i上的均布压力；
                Δi —— 基础以外荷载对矩形网格i的中点产生的沉降；
Mx、My、N —— 荷载对坐标原点的X、Y向总弯距和总竖向荷载。