| 功能说明 |
|
梁单元假设沿全长为等截面且具有三个平动自由度和三个旋转自由度。轴向刚度的计算方法与桁架单元相同,抗扭刚度的计算方法也类似于轴向刚度的计算方法。抗弯和抗剪刚度的计算使用了铁摩辛柯(Timoshenko)梁理论。 |
|
轴向刚度如下: |
|
|
|
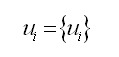 (2.3.2-1) (2.3.2-1) |
|
|
|
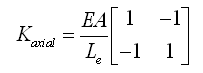 (2.3.2-2) (2.3.2-2) |
|
|
|
式中:
A
 截面面积; 截面面积;
Le
 单元长度。 单元长度。 |
|
抗扭刚度也可参照轴向刚度的计算方法可得: |
|
|
|
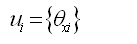 (2.3.2-3) (2.3.2-3) |
|
|
|
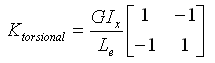 (2.3.2-4) (2.3.2-4) |
|
|
|
式中:
Ix
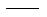 扭转常数(torsional
constant); 扭转常数(torsional
constant);
Le  单元长度。 单元长度。 |
|
|
|
抗剪和抗弯刚度是相关的,首先介绍基于铁摩辛柯梁理论的考虑剪切变形的刚度的计算方法。在单元坐标系x-z平面上表示剪切变形和弯曲变形的位移为沿在z方向的平动位移w和绕y轴的旋转位移θ。 |
|
|
|
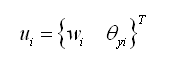 (2.3.2-5) (2.3.2-5) |
|
|
|
沿单元坐标系x轴上的任意点的坐标和位移w可用形函数表示如下: |
|
|
|
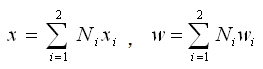 (2.3.2-6) (2.3.2-6) |
|
|
|
绕单元坐标系y轴的旋转角用二次方程表示如下: |
|
|
|
 (2.3.2-7) (2.3.2-7) |
|
|
|
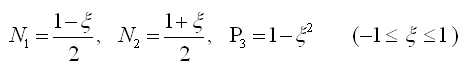 (2.3.2-8)
(2.3.2-8) |
|
|
|
为了计算单元中央的假想点的旋转角Δθy3使用了下列假定:
剪力和弯矩满足下列关系平衡关系: |
|
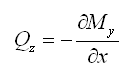 (2.3.2-9) (2.3.2-9) |
|
|
|
使用上面的平衡关系计算的平均剪切应变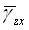 与由形函数计算的剪切应变 与由形函数计算的剪切应变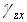 满足下列方程: 满足下列方程: |
|
|
|
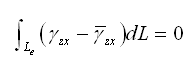 (2.3.2-10) (2.3.2-10) |
|
|
|
使用上述假定可得中央假想点的旋转角Δθy3如下: |
|
|
|
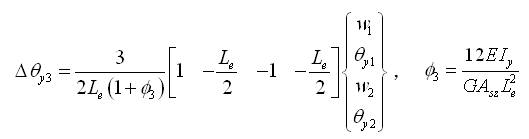 (2.3.2-11) (2.3.2-11) |
|
|
|
式中: |
|
Asx
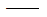 有效剪切面积; 有效剪切面积;
Iy
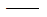 截面惯性矩。 截面惯性矩。 |
|
节点位移和曲率κy的关系使用矩阵Bbi表示如下: |
|
|
|
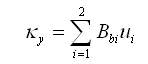 (2.3.2-12) (2.3.2-12) |
|
|
|
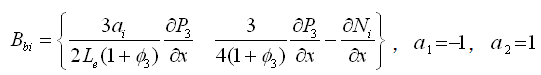 (2.3.2-13) (2.3.2-13) |
|
|
|
剪切变形使用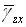 , ,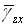 与节点位移的关系用Bsi表示如下: 与节点位移的关系用Bsi表示如下: |
|
|
|
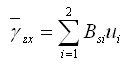 (2.3.2-14) (2.3.2-14) |
|
|
|
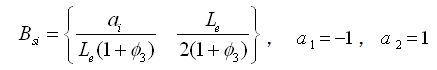 (2.3.2-15) (2.3.2-15) |
|
|
|
由此可得抗剪和抗弯刚度如下:
|
|
|
|
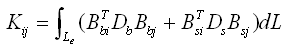 (2.3.2-16) (2.3.2-16) |
|
|
|
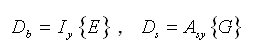 (2.3.2-17) (2.3.2-17) |
|
|
|
将式(2.3.2-16)积分整理可得x-z平面上的抗弯和抗剪刚度如下: |
|
|
|
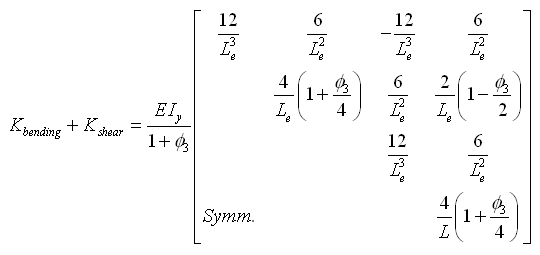 (2.3.2-18) (2.3.2-18) |
|
|
|
单元坐标系x-y平面上的抗弯和抗剪刚度也可按相同的方法获得。 |
|
|
