| 功能说明 |
|
假设平面应力单元的厚度不变,平面应力单元使用等参单元,四节点单元使用非协调模式。平面应力单元只有沿单元坐标系x、y方向的平动位移u、ν: |
|
|
|
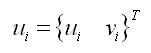 (2.5.2-1) (2.5.2-1) |
|
|
|
没有考虑非协调模式的单元内任意的坐标x、y和平动位移u、v使用形函数表示如下: |
|
|
|
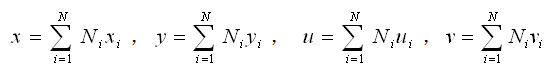 (2.5.2-2) (2.5.2-2) |
|
|
|
三节点单元的形函数 |
|
|
|
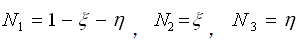 (2.5.2-3) (2.5.2-3) |
|
四边形单元的形函数 |
|
|
|
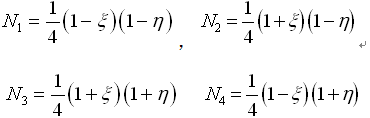 (2.5.2-4) (2.5.2-4) |
|
节点位移u与应变ε使用几何转换矩阵Bi表示如下: |
|
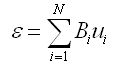 (2.5.2-5) (2.5.2-5) |
|
转换矩阵Bi可以使用形函数的微分表示如下: |
|
|
|
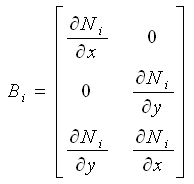 (2.5.2-6) (2.5.2-6) |
|
与面内变形相关的单元刚度矩阵如下: |
|
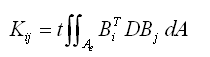 (2.5.2-7) (2.5.2-7) |
|
式中: |
|
t
 厚度; 厚度;
Ae
 面积。 面积。 |
|
各向同性材料的应力与应变的本构矩D如下: |
|
|
|
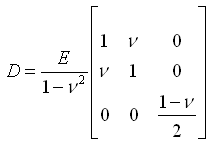 (2.5.2-8) (2.5.2-8) |
|
线性分析时,四节点单元使用非协调模式,除了节点位移以外会有下列其它自由度的位移: |
|
|
|
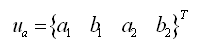 (2.5.2-9) (2.5.2-9) |
|
考虑非协调模式的节点坐标x、y和平动位移u、v如下: |
|
|
|
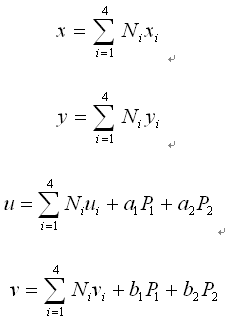 (2.5.2-10) (2.5.2-10) |
|
非协调模式的形函数如下: |
|
|
|
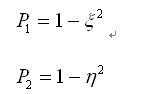 (2.5.2-11) (2.5.2-11) |
|
|
|
应变ε使用节点位移和非协调模式表示如下: |
|
|
|
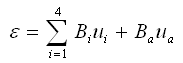 (2.5.2-12) (2.5.2-12) |
|
|
|
与非协调模式相关的转换矩阵Ba如下: |
|
|
|
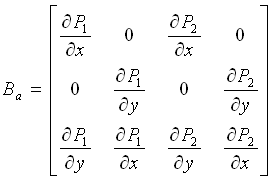 (2.5.2-13) (2.5.2-13) |
|
|
|
使用转换矩阵Bi和Ba计算面内刚度矩阵可得下面四个刚度矩阵: |
|
|
|
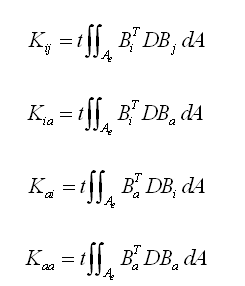 (2.5.2-14) (2.5.2-14) |
|
四个刚度矩阵的关系如下: |
|
|
|
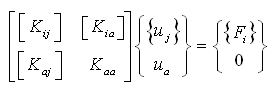 (2.5.2-15) (2.5.2-15) |
|
|
|
使用静力凝聚(static
condensation)方法消除非协调模式的刚度: |
|
|
|
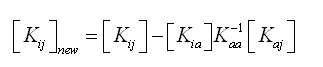 (2.5.2-16) (2.5.2-16) |
|
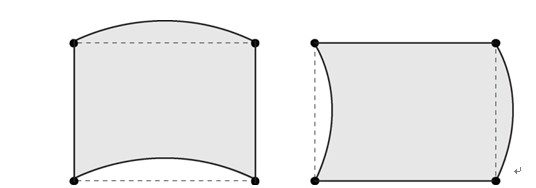
在计算与非协调模式相关的转换矩阵Ba时,微分中使用自然坐标系(natural coordinate)相对于原点(ξ=η=0)的雅可比转换。非协调模式可以模拟如图2.5.3所示的面内弯曲变形,所以可提高单元性能。
|
|
|
|
|
|
图2.5.2 非协调模式的形状(弯曲) |
|
|
