| 功能说明 |
|
反应谱分析的动力平衡方程如下: |
|
|
|
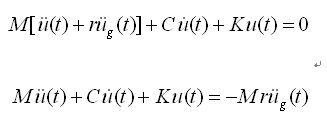 (4.5.2-1) (4.5.2-1) |
|
式中:
M
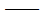 质量矩阵; 质量矩阵;
C
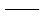 阻尼矩阵; 阻尼矩阵;
K
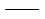 刚度矩阵; 刚度矩阵;
r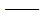 基底加速度向量; 基底加速度向量;
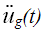 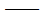 基底加速度时程; 基底加速度时程;
u(t)
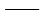 相对位移; 相对位移;
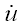 (t) (t)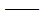 速度; 速度;
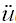 (t) (t)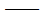 加速度。 加速度。
使用自由振动分析中获得的振型形状Φ和振型位移y(t)表示u(t)可得: |
|
|
|
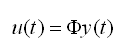 (4.5.2-2) (4.5.2-2) |
|
|
|
将式(4.5.2-2)代入式(4.5.2-1)后两边各乘ΦT可得: |
|
|
|
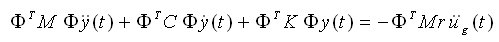 (4.5.2-3) (4.5.2-3) |
|
|
|
振型形状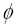 具有正交性,即满足下式: 具有正交性,即满足下式: |
|
|
|
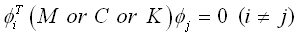 (4.5.2-4) (4.5.2-4) |
|
|
|
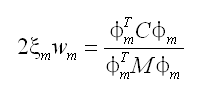 (4.5.2-5) (4.5.2-5)
|
|
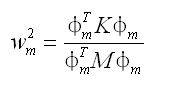 (4.5.2-6) (4.5.2-6)
|
|
|
|
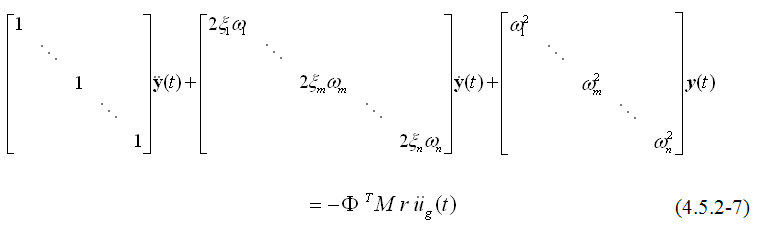
|
|
|
|
将式(4.5.2-7)表现为第m振型的公式可得: |
|
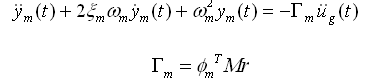 (4.5.2-8) (4.5.2-8) |
|
|
|
式(4.5.2-8)中的振型参与系数Γm是使用了用质量归一化的振型形状、节点质量、基底加速度的乘积。基底加速度的方向向量是单位方向向量。解(4.5.2-8)得n个方程的解后按下面式(4.5.2-9)进行组合: |
|
|
|
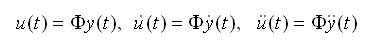 (4.5.2-9) (4.5.2-9) |
|
|
|
反应谱分析不是使用基底加速度函数,而是使用谱函数计算各振型的结果。谱函数为式(4.5.2-7)的各周期的最大值(地震影响系数),设计规范一般考虑地震的强度和近远震的影响、建筑的重要性等综合因素提供了设计谱函数。任意第m振型的位移、速度、加速度可按下式表示: |
|
|
|
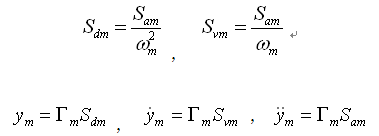 (4.5.2-10) (4.5.2-10) |
|
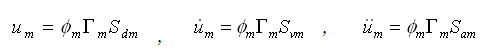 (4.5.2-11) (4.5.2-11) |
|
|
|
式中:
Sdm
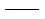 第m振型的位移谱值; 第m振型的位移谱值;
Svm  第m振型的速度谱值; 第m振型的速度谱值;
Sam
 第m振型的加速度谱值。 第m振型的加速度谱值。
因为各振型的结果都是最大值,所以无法像时程分析那样线性组合各时刻的结果。结构大师中提供了SRSS(square root
of the sum of the squares)法和CQC(complete quadratic combination)法。 |
|
|
|
SRSS
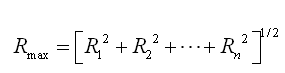 (4.5.2-12) (4.5.2-12) |
|
|
|
CQC
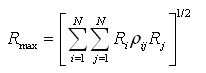 (4.5.2-13) (4.5.2-13) |
|
|
|
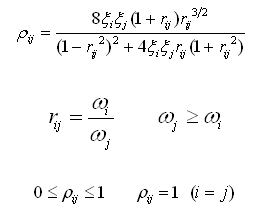
|
|
式中:
Rmax
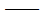 最终效应结果; 最终效应结果;
Ri 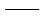 第i振型的谱值; 第i振型的谱值;
rij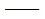 对第i振型的第j振型的特征值比值; 对第i振型的第j振型的特征值比值;
ωi、ωj 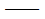 第i、j振型的特征值; 第i、j振型的特征值;
ξi、ξj
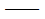 第i、j振型的阻尼比; 第i、j振型的阻尼比;
ρij
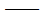 第i、j振型间的耦联系数(correlation
coefficient)。 第i、j振型间的耦联系数(correlation
coefficient)。
当i=j时,与阻尼比(ξi、ξj)无关始终有ρij=1;当阻尼比为0时,CQC的结果和SRSS相同。 |
|
|
