| 功能说明 |
|
振型分解法利用振型的正交性,将式(4.6.1-1)转化为独立的各振型的方程。为了使用振型分解法,需要假设结构的阻尼矩阵,可以用结构的刚度矩阵和质量矩阵的线性组合表达。求得各振型的响应后,再用下面公式进行线性组合。 |
|
|
|
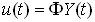 (4.6.2-1) (4.6.2-1) |
|
|
|
将式(4.6.2-1)代入式(4.6.1-1)可得: |
|
|
|
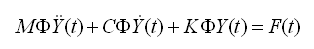 (4.6.2-2) (4.6.2-2)
|
|
|
|
在式(4.6.2-2)两边乘ΦmT(第m振型形状)可得:
|
|
|
|
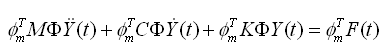 (4.6.2-3) (4.6.2-3)
|
|
|
|
特征模态的质量矩阵和刚度矩阵的正交性可用下式表示: |
|
|
|
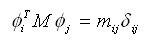 (4.6.2-4) (4.6.2-4) |
|
|
|
式中:
δij 克罗内克符号(Kronecker
delta) (i=j,δij=1;否则,δij=0)。 克罗内克符号(Kronecker
delta) (i=j,δij=1;否则,δij=0)。
利用模态对于质量和刚度矩阵的正交性,可将动力平衡方程式(4.6.2-3)分解为下面n个互相独立的方程式: |
|
|
|
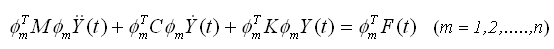 (4.6.2-5) (4.6.2-5) |
|
|
|
上面的n个方程就是在广义坐标系(general
coordinate)的多自由度体系的动力平衡方程。可将式(4.6.2-5)重新表示为如下公式: |
|
|
|
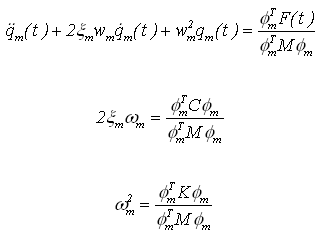 (4.6.2-6) (4.6.2-6)
|
|
式中:
ζm
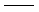 第m振型的阻尼比; 第m振型的阻尼比;
ωm
 第m振型的特征频率; 第m振型的特征频率;
qm(t)
 第m振型的广义位移; 第m振型的广义位移;
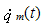  第m振型的速度; 第m振型的速度;
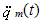 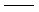 第m振型的加速度。 第m振型的加速度。 |
|
|
|
在广义坐标系下的位移响应如下: |
|
|
|
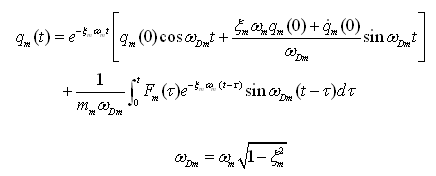 (4.6.2-7) (4.6.2-7) |
|
|
|
将各振型的广义位移结果代入式(4.6.2-7)可得结构的位移响应。
振型分解法结果的精确度受到振型数量的影响。振型分解法在解大型结构的线弹性时程分析中非常高效实用,但是不适于考虑材料非线性的动力弹塑性问题和包含消能减震装置的动力问题。 |
|
|
