| 功能说明 |
|
直接积分法是将分析时间长度分割为多个微小的时间间隔,用数值积分方法解微小时间间隔的动力平衡方程的动力分析方法。直接积分法可以解刚度和阻尼的非线性问题,但是随着分析步骤的增加分析时间会较长。
数值积分方法有很多,结构大师中提供Newmark-β法解动力方程。结构大师中Newmark-β法中有常加速度法(平均加速度法)、线性加速度法以及用户输入参数的方法。下面介绍平均加速度法。设在ti时刻和ti+1时刻的加速度分别为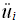 和 和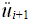 ,平均加速度法假定在ti<t<ti+1时间区段内的加速度为 ,平均加速度法假定在ti<t<ti+1时间区段内的加速度为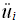 和 和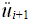 的平均值。 的平均值。 |
|
|
|
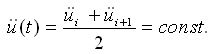 (4.6.3-1) (4.6.3-1) |
|
|
|
因此,在时刻ti+1的速度和位移如下: |
|
|
|
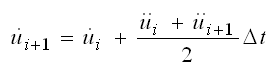 (4.6.3-2) (4.6.3-2) |
|
|
|
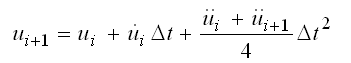 (4.6.3-3) (4.6.3-3) |
|
|
|
将式(4.6.3-2)和(4.6.3-3)用Newmark-β法的积分参数表达如下: |
|
|
|
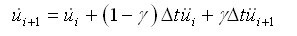 (4.6.3-4) (4.6.3-4) |
|
|
|
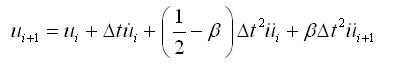 (4.6.3-5) (4.6.3-5) |
|
|
|
式中:
β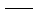 0.25; 0.25;
γ
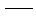 0.5。 0.5。
将式(4.6.3-5)整理如下: |
|
|
|
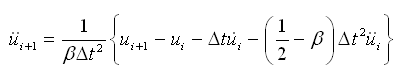 (4.6.3-6) (4.6.3-6) |
|
|
|
将式(4.6.3-4)代入式(4.6.3-6)并整理成速度的公式如下: |
|
|
|
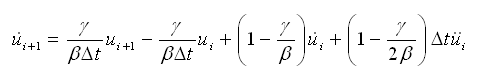 (4.6.3-7) (4.6.3-7) |
|
|
|
将式(4.6.3-6)和(4.6.3-7)代入动力平衡方程得时刻ti+1时的位移响应ui+1如下: |
|
|
|
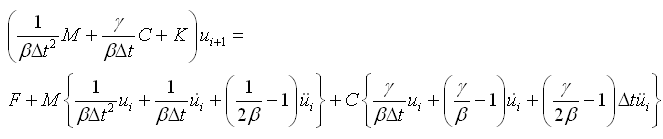
(4.6.3-8) |
|
|
|
将时刻ti+1的位移ui+1代入式(4.6.3-6)和(4.6.3-7)可得速度和加速度。
直接积分法的阻尼使用瑞利阻尼: |
|
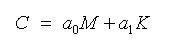 (4.6.3-9) (4.6.3-9) |
|
|
|
式中:
a0
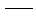 质量比例因子; 质量比例因子;
a1
 刚度比例因子。 刚度比例因子。
将式(4.6.3-9)代入(4.6.3-8)可得: |
|
|
|
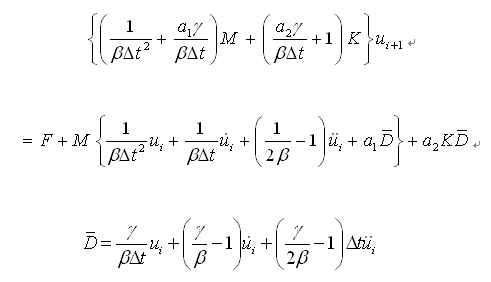 (4.6.3-10) (4.6.3-10)
|
|
|
|
通过时程分析计算的位移、速度、加速度为相对位移u(t)、相对速度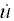 (t)、相对加速度 (t)、相对加速度 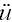 (t)。当结构受地面运动的作用时,结构的绝对响应可通过叠加相对响应和地面运动计算。 (t)。当结构受地面运动的作用时,结构的绝对响应可通过叠加相对响应和地面运动计算。 |
|
绝对加速度:
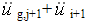
绝对速度:
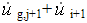
绝对位移:
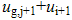 (4.6.3-11) (4.6.3-11) |
|
式中:
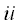 g,j+1 g,j+1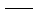 地面加速度; 地面加速度;
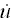 g,j+1 g,j+1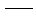 地面速度; 地面速度;
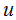 g,j+1 g,j+1 地面位移。 地面位移。 |
|
|
|
结构大师中使用地面加速度计算地面速度和地面位移的方法如下: |
|
|
|
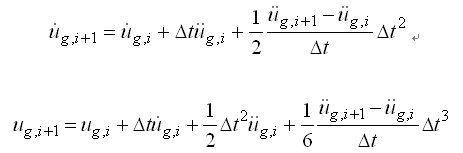 (4.6.3-12) (4.6.3-12)
|
|
|
|
|
