| 功能说明 |
1. 型钢混凝土框架梁,其正截面受弯承载力应按下列假定进行计算:
(1)截面应变保持平面
(2)不考虑混凝土的抗拉强度
(3)混凝土受压的应力与应变关系曲线按下列规定取用:
当εc≤ε0时
|
|
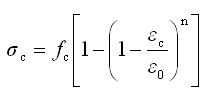 (5.2.8-1) (5.2.8-1)
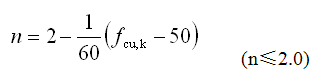 (5.2.8-2) (5.2.8-2)
|
|
当ε0<εc≤εcu时 |
|
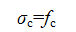 (5.2.8-3) (5.2.8-3)
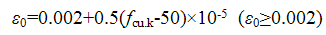 (5.2.8-4) (5.2.8-4)
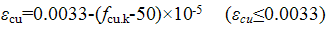 (5.2.8-5) (5.2.8-5)
|
|
式中:
σc
—— 混凝土压应变为εc时的混凝土压应力;
fc
—— 混凝土轴心抗压强度设计值;
ε0 —— 混凝土压应力刚达到fc时的混凝土压应变;
εcu
—— 正截面混凝土极限压应变,当处于非均匀受压时,按公式(5.2.8-4)计算;当处于轴心受压时取为ε0;
fcu,k
—— 混凝土立方体抗压强度标准值;
n
—— 系数。 |
|
(4)纵向受拉钢筋的极限应变取为0.01,纵向受拉钢筋的应力取等于钢筋应变与其弹性模量的乘积,纵向钢筋的应力可按下式计算:
|
|
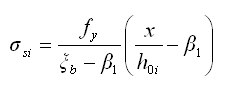 (5.2.8-6) (5.2.8-6)
|
|
按公式(5.2.8-6)计算的纵向钢筋应力应符合下列条件: |
|
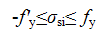 (5.2.8-7) (5.2.8-7)
|
|
当计算的σsi为拉应力且其值大于fy时,取σsi=fy;当σsi为压应力且其绝对值大于
f 'y时,取σsi=-f 'y 。 |
|
式中:
σsi
—— 第i层纵向钢筋的应力,正值代表拉应力,负值代表压应力;
h0i
—— 第i层纵向钢筋截面重心至截面受压边缘的距离;
x
—— 等效矩形应力图形混凝土压应力刚达到fc时的混凝土压应变;
εcu
—— 正截面混凝土极限压应变,当处于非均匀受压时,按公式(5.2.8-4)计算;当处于轴心受压时取为ε0;
fcuk
—— 混凝土立方体抗压强度标准值;
n
—— 系数。 |
|
(5)型钢腹板的应力图为拉、压梯形应力图形。设计计算时,简化为等效矩形应力图形;
2. 型钢截面为充满型实腹型钢的型钢混凝土框架梁,其正截面受弯承载力应按下列公式计算:
(1)非抗震设计 |
|
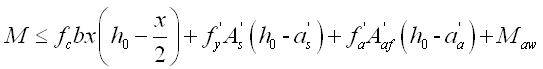 (5.2.8-8) (5.2.8-8)
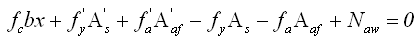 (5.2.8-9) (5.2.8-9)
|
|
(2)抗震设计 |
|
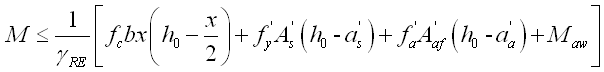 (5.2.8-10) (5.2.8-10)
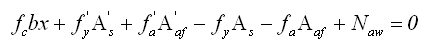 (5.2.8-11) (5.2.8-11)
|
|
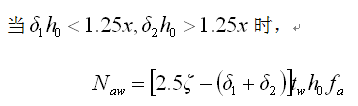 (5.2.8-12) (5.2.8-12)
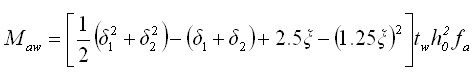 (5.2.8-13) (5.2.8-13)
|
|
混凝土受压区高度x尚应符合下列公式要求: |
|
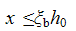 (5.2.8-14) (5.2.8-14)
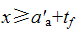 (5.2.8-15) (5.2.8-15) |
|
式中:
ζ —— 相对受压区高度;
ζb
—— 相对界限受压区高度;
xb
—— 界限受压区高度;
Maw —— 型钢腹板承受的轴向合力对受拉翼缘和纵向受拉钢筋合力点的力矩;
Naw
—— 型钢腹板承受的轴向合力;
δ1
—— 型钢腹板上端至截面上边距离与h0的比值;
δ2
—— 型钢腹板下端至截面上边距离与h0的比值;
tw
—— 型钢腹板厚度;
tf —— 型钢翼缘厚度;
hw
—— 型钢腹板高度;
h
—— 型钢受拉翼缘和纵向受拉钢筋合力点至混凝土受压边缘的距离。 |
|
3. 型钢混凝土框架梁,其斜截面受剪承载力应按下列假定进行计算:
(1)型钢混凝土框架梁考虑抗震等级的剪力设计值Vb,应按如下计算:
一级抗震等级: |
|
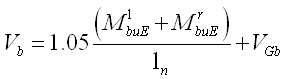 (5.2.8-16) (5.2.8-16)
|
|
二级抗震等级: |
|
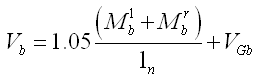 (5.2.8-17) (5.2.8-17) |
|
三级抗震等级: |
|
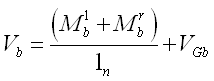 (5.2.8-18) (5.2.8-18)
|
|
式中:
MlbuE、MrbuE
—— 框架梁左、右端采用实配和实配型钢、强度标准值,且考虑承载力抗震调整系数的正截面受弯承载力所对应的弯矩值;
Mlb、Mrb
—— 考虑地震作用组合的框架梁左、右端弯矩设计值相对界限受压区高度;
VGb
—— 考虑地震作用组合的重力荷载代表值产生的剪力设计值,可按简支梁计算确定;
ln
—— 梁的净跨。 |
|
在公式(5.2.8-9)~(5.2.8-11)中,MlbuE和MrbuE之和,以及Mlb和Mrb之和,应分别按顺时针和逆时针方向进行组合,并取其较大值。
(2)型钢混凝土框架梁的受剪截面应符合下列规定:
① 非抗震设计 |
|
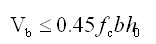 (5.2.8-19) (5.2.8-19)
|
|
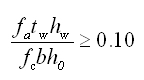 (5.2.8-20) (5.2.8-20)
|
|
②
抗震设计 |
|
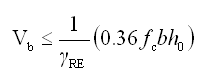 (5.2.8-21) (5.2.8-21)
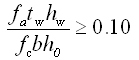 (5.2.8-22) (5.2.8-22)
|
|
(3)型钢混凝土框架梁的斜截面承载力应按下列公式计算:
① 非抗震设计 |
|
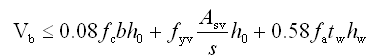 (5.2.8-23) (5.2.8-23)
|
|
②
抗震设计 |
|
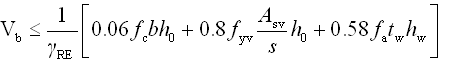 (5.2.8-24) (5.2.8-24)
|
|
4. 型钢混凝土框架梁正常使用极限状态验算
(1)型钢混凝土框架梁裂缝宽度验算
型钢混凝土框架梁最大裂缝宽度应按荷载的短期效应组合并考虑长期效应组合的影响进行计算。计算公式如下所示: |
|
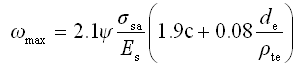 (5.2.8-25) (5.2.8-25)
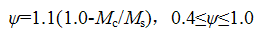 (5.2.8-26) (5.2.8-26)
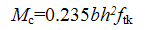 (5.2.8-27) (5.2.8-27)
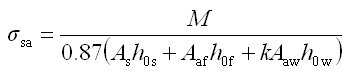 (5.2.8-28) (5.2.8-28)
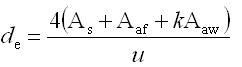 (5.2.8-29) (5.2.8-29)
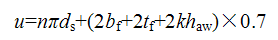 (5.2.8-30) (5.2.8-30)
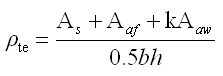 (5.2.8-31) (5.2.8-31)
|
|
式中:
c
—— 纵向受拉钢筋的混凝土保护层厚度;
ψ
—— 相对界限受压区高度考虑型钢翼缘作用的钢筋应变不均匀系数;当ψ<0.4时ψ=0.4;当ψ>1.0时ψ=1.0;
k
—— 考型钢腹板影响系数,其值取梁受拉侧1/4梁高范围中腹板高度与整个腹板高度的比值;
de、ρte
—— 型钢受拉翼缘与部分腹板及受拉钢筋的有效直径、有效配筋率;
σsa
—— 考虑型钢受拉翼缘与部分腹板及受拉钢筋的钢筋应力值;
Mc
—— 混凝土截面的抗裂弯矩;
As、Aaf —— 纵向受力钢筋、型钢受拉翼缘面积;
Aaw、haw —— 型钢腹板面积、高度;
h0s、h0f、h0w
—— 纵向受拉钢筋、型钢受拉翼缘、KAaw截面重心至混凝土截面受压边缘的距离;
n
—— 纵向受拉钢筋数量;
u、h
—— 型纵向受拉钢筋和型钢受拉翼缘与部分腹板周长之和。
|
|
(2)型钢混凝土框架梁挠度验算
型钢混凝土框架梁在正常使用极限状态下的挠度,可根据构件的刚度用结构力学的方法计算。在等截面构件中,可假定各同号弯矩区段内的刚度相等,并取用该区段内最大弯矩处的刚度。受弯构件的挠度应按荷载短期效应组合并考虑长期效应组合影响的长期刚度B1进行计算,所求得的挠度计算值不应大于规范限值。
当型钢混凝土框架梁的纵向受拉钢筋配筋率为0.3%~1.5%范围时,其荷载短期效应和长期效应组合作用下的短期刚度Bs和长期刚度B1,按下列公式计算: |
|
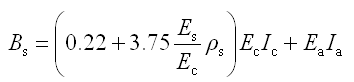 (5.2.8-32) (5.2.8-32)
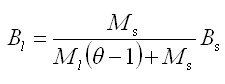 (5.2.8-33) (5.2.8-33)
|
|
式中:
Ec
—— 混凝土弹性模量;
Ea
—— 型钢弹性模量;
Ic
—— 按截面尺寸计算的混凝土截面惯性矩;
Ia
—— 型钢的截面惯性矩;
Ms
—— 按荷载短期效应组合计算的弯矩值;
Ml
—— 按荷载长期效应组合计算的弯矩值;
θ
—— 考虑荷载长期效应组合对挠度增大的影响系数。 |
|
|
 |
|
1 |

|
|
|
