| 功能说明 |
|
特征值分析是分析结构固有振动特性的分析方法,又称为无阻尼自由振动分析。特征值分析是反应谱分析和振型分解时程分析前必须做的分析。
特征值分析的运动方程式如下: |
|
|
|
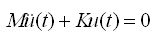 (4.4.1-1) (4.4.1-1)
|
|
|
|
式中:
K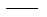 结构的刚度矩阵; 结构的刚度矩阵;
M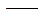 结构的质量矩阵。 结构的质量矩阵。
将位移u使用形函数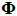 和时间向量Y(t)的乘积u= 和时间向量Y(t)的乘积u=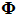 Y(t)表现,则可得下面公式: Y(t)表现,则可得下面公式: |
|
|
|
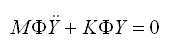 (4.4.1-2) (4.4.1-2)
|
|
|
|
将时间函数Y(t)用下列向量表示: |
|
|
|
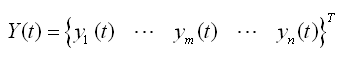 (4.4.1-3) (4.4.1-3) |
|
|
|
式中:
n
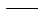 总自由度数; 总自由度数;
ym(t) cos(wmt+βm)。 cos(wmt+βm)。
将式(4.4.1-3)代入(4.4.1-2)可得: |
|
|
|
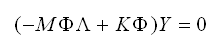 (4.4.1-4) (4.4.1-4) |
|
|
|
矩阵Λ和Ф如下: |
|
|
|
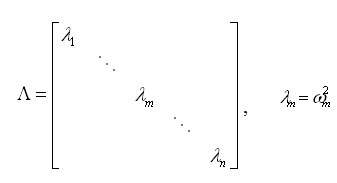 (4.4.1-5) (4.4.1-5)
|
|
|
|
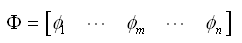 (4.4.1-6) (4.4.1-6) |
|
|
|
对各ym(t)需要满足式(4.4.1-4),则可得: |
|
|
|
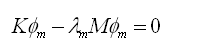 (4.4.1-7) (4.4.1-7)
|
|
|
|
式(4.4.1-7)即为解特征值的方程,为了获得有意义的解需要满足下式: |
|
|
|
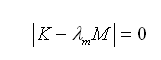 (4.4.1-8) (4.4.1-8)
|
|
|
|
质量矩阵M和刚度矩阵K是对称矩阵,特征值λm和特征向量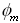 为实数。当没有外部荷载作用时,结构按特征向量 为实数。当没有外部荷载作用时,结构按特征向量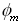 的形状振动,其振动的速度用圆频率ωm
(radian/time)或固有频率fm(cycle/time)和固有周期tm(time/cycle)表示。ω、fm、Tm的相互关系如下: 的形状振动,其振动的速度用圆频率ωm
(radian/time)或固有频率fm(cycle/time)和固有周期tm(time/cycle)表示。ω、fm、Tm的相互关系如下: |
|
|
|
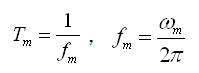 (4.4.1-9) (4.4.1-9)
|
|
|
|
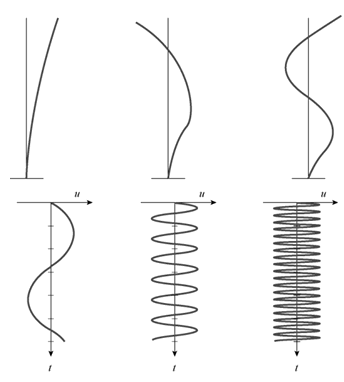
特征值λm为第m振型的应变能和动能的比值,从小到到大依次称为第一振型、第二振型、...、第n振型。下图4.4.1显示的是悬臂梁的振型形状示意图。 |
|
|
|
图4.4.1 悬臂梁的振型形状示意图 |
|
|
|
结构大师还提供反映结构振动特性的振型周期、振型参与系数、振型方向系数和特征向量等参数。
振型参与系数按下面公式计算,被应用于反应谱分析和时程分析中。 |
|
|
|
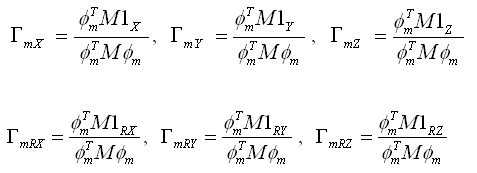 (4.4.1-10) (4.4.1-10)
|
|
|
|
式中:
ГmX、ГmY、ГmZ
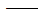 弹性刚度矩阵; 弹性刚度矩阵;
ГmRX、ГmRY、ГmRZ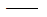 每次通过迭代计算得到的几何刚度矩阵; 每次通过迭代计算得到的几何刚度矩阵;
Ix、Iy、Iz
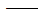 静力荷载向量; 静力荷载向量;
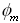 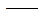 位移向量。 位移向量。 |
|
振型参与质量等于该振型质量(或称为模态质量)乘以该振型的振型参与系数的平方,由式4.4.1-10可得振型参与质量计算公式如下。因为振型有正负号,所以振型参与质量有可能为零。所有振型的参与质量之和为结构的总有效质量,当结构的节点质量没有被约束时,总有效质量和结构的总质量相同。 |
|
|
|
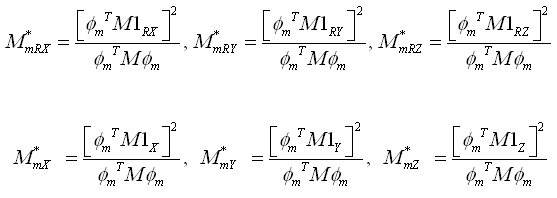 (4.4.1-11) (4.4.1-11)
|
|
|
|
式中:
Mmx、Mmy、Mmz
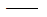 第m振型在x、y、z平动方向的振型参与质量; 第m振型在x、y、z平动方向的振型参与质量;
MmRx、MmRy、MmRz
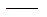 第m振型在x、y、z轴旋转方向的振型参与质量。 第m振型在x、y、z轴旋转方向的振型参与质量。
振型参与质量系数为各振型的参与质量与总有效质量的比值,《抗规》GB50011-2001规定在反应谱分析中,考虑的振型数量的质量参与系数之和要达到90%以上。这是为了保证地震作用的计算精度。
结构大师中提供了两种求解特征值方程的方法,即兰佐斯法 和子空间迭代法。兰佐斯法的计算速度较快,适合于解大型工程的特征值问题;子空间迭代法计算比较稳定,适合求解各种工程的特征值问题。 |
|
|
|
|
