等截面焊接工字形和轧制H型钢（图B.1）简支梁的整体稳定系数应按下式计算：
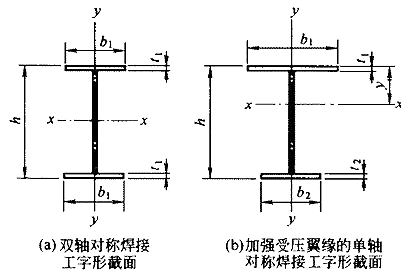
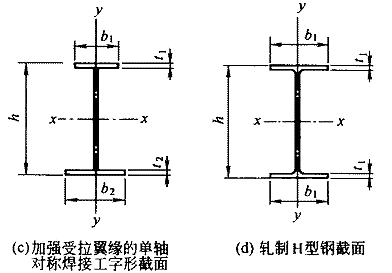
图 B.1 焊接工字形和轧制H型钢截面
(B.1-1)
式中
: 梁整体稳定的等效临界弯矩系数，按表B.1采用
: 梁在侧向支承点间对截面弱轴y-y的长细比，
,
见本规范第4.2.1条，
为梁毛截面对y轴的截面回转半径
:
梁的毛截面面积；
、
: 梁截面的全高和受压翼缘厚度
: 截面不对称影响系数；对双轴对称截面（图B1a、d）：
；对单轴对称工字形截面（图B.1b、c）：加强受压翼缘：
；加强受
拉翼缘： ；
，，式中
和
分别为受压翼缘和受拉翼缘对y轴的惯性矩。
当按公式(B.1-1)算得的值大于0.6时，应用下式计算的
代替
值：
(B.1-2)
※注：
公式（B.1-1）亦适用于等截面铆接（或高强度螺栓连接）简支梁，其受压翼缘厚度t1包括翼缘角钢厚度在内。
轧制普通工字钢简支梁的整体稳定系数应按表B.2采用，当所得的
值大于0.6时，应按公式（B.1-2）算得相应的
代替
值。
表B.2
|
轧制普通工字钢简支梁的φb |
|||||||||||||||||||||
|
项次 |
荷载情况 |
工字钢 型 号 |
自由长度l1(m) |
||||||||||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 | |||||||||||||
|
1 |
跨 中 无 侧 向 支 撑 点 的 梁 |
集 中 荷 载 作 用 与 |
上 翼 缘 |
10～20 |
2.00 |
1.30 |
0.99 |
0.80 |
0.68 |
0.58 |
0.53 |
0.48 |
0.43 | ||||||||
|
22～32 |
2.40 |
1.48 |
1.09 |
0.86 |
0.72 |
0.62 |
0.45 |
0.49 |
0.45 | ||||||||||||
|
36～63 |
2.80 |
1.6 |
1.07 |
0.83 |
0.68 |
0.56 |
0.50 |
0.45 |
0.40 | ||||||||||||
|
2 |
下 翼 缘 |
10～20 |
2.80 |
1.60 |
1.07 |
0.83 |
0.68 |
0.56 |
0.50 |
0.45 |
0.40 | ||||||||||
|
22～40 |
3.10 |
1.95 |
1.34 |
1.01 |
0.82 |
0.69 |
0.63 |
0.57 |
0.52 | ||||||||||||
|
45～63 |
5.50 |
2.80 |
1.84 |
1.37 |
1.07 |
0.86 |
0.73 |
0.64 |
0.56 | ||||||||||||
|
3 |
均 布 荷 载 作 用 于 |
上 翼 缘 |
10～20 |
1.70 |
1.12 |
0.84 |
0.68 |
0.57 |
0.50 |
0.45 |
0.41 |
0.37 | |||||||||
|
22～40 |
2.10 |
1.30 |
0.93 |
0.73 |
0.60 |
0.51 |
0.45 |
0.40 |
0.36 | ||||||||||||
|
45～63 |
2.60 |
1.45 |
0.97 |
0.73 |
0.59 |
0.50 |
0.44 |
0.38 |
0.35 | ||||||||||||
|
4 |
上 翼 缘 |
10～20 |
2.50 |
1.55 |
1.08 |
0.83 |
0.68 |
0.56 |
0.52 |
0.47 |
0.42 | ||||||||||
|
22～40 |
4.00 |
2.20 |
1.45 |
1.10 |
0.85 |
0.70 |
0.60 |
0.52 |
0.46 | ||||||||||||
|
45～63 |
5.60 |
2.80 |
1.80 |
1.25 |
0.85 |
0.78 |
0.65 |
0.55 |
0.49 | ||||||||||||
|
5 |
跨中有侧向支撑点 的梁（不论荷载作用 点在截面高度上的位置） |
10～20 |
2.20 |
1.39 |
1.01 |
0.79 |
0.66 |
0.57 |
0.52 |
0.47 |
0.42 | ||||||||||
|
22～40 |
3.00 |
1.80 |
1.24 |
0.96 |
0.76 |
0.65 |
0.56 |
0.49 |
0.43 | ||||||||||||
|
45～63 |
4.00 |
2.20 |
1.38 |
1.01 |
0.80 |
0.66 |
0.56 |
0.49 |
0.43 | ||||||||||||
※注：
1. 同表B.1的注3.5
2. 表中的φb适用于Q235钢。对其他钢号，表中数值应乘以235/fy。
轧制槽钢简支梁的整体稳定系数，不论荷载的形式和荷载作用点在截面高度上的位置，均可按下式计算：
（B.3）
式中
、
、
：分别为槽钢截面的高度、翼缘跨度和平均厚度
按公式（B.3）算得的值大于0.6时，应按公式（B.1-2）计算的
代替
值。
双轴对称工字形等截面（含H型钢）悬臂梁的整体稳定系数，可按公式（B.1-1）计算，但式中系数应按表B.4查得
（l为悬臂梁的悬伸长度）。当求得的
值大于0.6时，应按公式（B.1-2）计算的
代替
值。
表 B.4
|
双轴对称工字形等截面（含H型钢）悬臂梁的系数βb |
|||||
|
项次 |
荷载形式 |
0.6≤ξ≤1.24 |
1.24≤ξ≤1.96 |
1.96≤ξ≤3.10 | |
|
1 |
自由端一个集中荷载作用在 |
上翼缘 |
0.21+0.67ξ |
0.72+0.26ξ |
1.17+0.03ξ |
|
2 |
下翼缘 |
0.94-0.65ξ |
2.64-0.40ξ |
2.15-0.15ξ | |
|
3 |
均布荷载作用在上翼缘 |
0.62+0.82ξ |
1.25+0.31ξ |
1.66+0.10ξ | |
※注：
1. 本表是按支承端为固定的情况确定的。当用于由邻跨延伸出来的伸出来的伸臂梁时，应在构造上采取措施施加
强支承处的抗扭能力。
2. 表中ξ见表B.1注1。
均匀弯曲的受弯构件，当时，其整体稳定系数
可按下列近似公式计算：
1. 工字形截面（含H型钢）：
双轴对称时：
(B.5-2)
单轴对称时：
(B.5-2)
2. T形截面（弯矩作用在对称轴平面，绕x轴）：
1) 弯矩使翼缘受压时：
双角钢T形截面：
(B.5-3)
剖分T型钢和两板组合T形截面：
(B.5-4)
2) 弯矩使翼缘受拉且腹板宽厚比不大于时：
(B.5-5)
按公式（B.5-1）至公式（B.5-5）算得的值大于0.6时，不需按公式（B.1-2）换算成
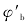，当按公式（B.5-1）和公式（B.5-2）算得的值大于1.0时，取
=1.0