本节对梁腹板局部稳定计算有较大变动,主要是:
1. 对原来按无限弹性计算的腹板各项临界应力作了弹塑性修正;
2. 修改了设置横向加劲肋的区格在几种应力共同作用下的临界条件;
3. 无局部压应力且承受静力荷载的工字形截面梁推荐按新增的4.4节利用腹板屈曲后强度;
4. 对轻、中级工作制吊车梁,为了适当考虑腹板局部屈曲后强度的有利影响,故吊车轮压设计值可乘以折减系数0.9。
4.3.2
需要配置纵向加劲肋的腹板高厚比,由原来硬性规定的界限值改为根据计算需要配置。但仍然给出高厚比的限值,并按梁受压翼缘扭转受到约束与否分为两档,
即:和
还增加了在任何情况下高厚比不应超过250的规定,以免高厚比过大时产生焊接翘曲。
4.3.3
多种应力作用下原用的临界条件公式来源于完全弹性条件。新的公式(4.3.3-1)参考了澳大利亚规范等资料,适合于弹塑性修正后的临界应力。
单项临界应力、
、
,
各有三个计算公式,如
为(4.3.3-2a、b、c)三个式子(图6)。
其中第一个为临界应力等于强度设计值;第三个为完全弹性的临界应力,而第二个则为弹性屈曲到屈服之间的过渡。虽然三个公式在形式上都以钢材强度设计值(或
)为准,但第三个式子的
(或
)乘以1.1后相当于
(或
),亦即不计抗力分项系数。弹性和非弹性范围区别对待的原因,是当板处于弹性范围时存在较大的屈曲后强度,安全系数可以小一些,只保留荷载分项系数就够了。早在编制TJ17-74规范时,一般安全系数为1.41,而腹板稳定的安全系数为1.25,相当于前者的1/1.13。第三个式子采用系数1.1,才能使本规范的弹性临界应力不低于74和88规范。
公式采用国际上通行的表达方式,即以通用高厚比(正则化宽厚比):
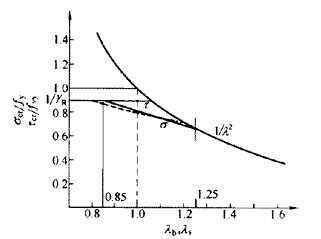
图 6 临界应力与通用高厚比关系曲线
或作为参数使同一公式通用于各个牌号的钢材。
它和压杆稳定计算的具有同样性质。以弯曲正应力为例,在弹性范围临界应力即为
用强度设计值表达,可取
。
把临界应力 代入,并取
,
对于受弯腹板,k=23.9,并取嵌固系数x=1.66和1.23(分别相当于梁翼缘扭转受约束和未受约束),代替原来的单一系数1.61,得:k=23.9,并取嵌固系数x=1.66和1.23(分别相当于梁翼缘扭转受约束和未受约束),代替原来的单一系数1.61,得:
和
对没有缺陷的板,当
时临界应力等于屈服点。
考虑残余应力和几何缺陷影响,取为弹塑性修正的上起始点,
相应的高厚比为:和
此高厚比比4.3.2条是否需要设置纵向加劲肋的高厚比限值小。这是由于需要计算腹板局部稳定的通常是吊车梁(一般梁推荐利用屈曲后强度,可不必设置纵向加劲肋),在横向水平力和竖向荷载共同作用下,腹板上边缘的弯曲压应力仅为强度设计值f的0.8~0.85倍,腹板高厚比虽达到上述高厚比,往往也不需要设置纵向加劲肋。=0.85也是4.4.1条考虑腹板屈曲后强度时截面是否全部有效的分界点。
弹塑性过渡段采用直线式(4.3.3-2b)比较简便。其下起始点参照梁整体稳定计算,弹性界限为,相应的
。考虑到腹板局部屈曲受残余应力影响不如整体届曲大,故取
=1.25
腹板在弯矩作用下屈曲,是压应力引起的。因此,对单轴对称的工字形截面梁,在计算时以2h代替ho。
、
,
情况和
类似,但单轴对称截面仍以ho为准。这两个临界应力的计算公式中,嵌固系数均保留原规范的数值,故不区分受压翼缘扭转是否受到约束。
4.3.4
有纵向加劲肋时,多种应力作用下的临界条件也有改变。受拉翼缘和纵向加劲肋之间的区格,相关公式和仅设横向加劲肋者形式上相同,而受压翼缘和纵向加劲肋之间的区格则在原公式的基础上对局部压应力项加上平方。这一区格的特点是高度比宽度小很多,和
(或
)的相关曲线上凸得比较显著。单项临界应力的计算公式都和仅设横向加劲肋时一样,只是由于屈曲系数不同,通用高厚比的计算公式有些变化。
在公式(9)中,代入屈曲系数k=5.13,并取x=1.4和1.0(分别相当于翼缘扭转受到约束和未受到约束),即得计算式[规范公式(4.3.4-2a、b)]中分母
和64代入
和
,则得
表达式[规范公式(4.3.4-5)]中分母
对局部横向压应力作用下,原规范对板段Ⅱ中
的计算公式(附2.12)与仅有横向肋时的
计算公式(附2.3)形式一致,只是区格高度不同。因此,修改后的
也采用与
相同的计算公式,但把ho改为h2.但原规范中对板段Ⅰ中的
的计算公式和仅有横向肋时
的计算公式没有联系且比较复杂,算得的结果都大于屈服点,需要另觅计算公式。由于区格Ⅰ宽高比常在4以上,宜作为上下两边支承的均匀受压板看待,取腹板有效宽度为h1的2倍。当受压翼缘扭转未受到约束时,上下两端均视为铰支,计算长度为h1;扭转受到完全约束时,则计算长度取0.7h1。规范公式(4.3.4-3a、b)就是这样得出的。
4.3.5
在受压翼缘与纵向加劲肋之间设置短加劲肋使腹板上部区格宽度减小,对弯曲压应力的临界值并无影响。对剪应力的临界值虽有影响,仍可用仅设横向加劲肋的临界应力公式计算。计算时以区格高度h1和宽度a1代替ho和a。影响最大的是横向局部压应力的临界值,需要用式(4.3.5)代替(4.3.4-3)来计算,原因是仅设纵向加劲肋时,腹板区格为一窄条,接近两边支承板,而设置短加劲肋后成为四边支承板,压应力临界值得到提高。当
时,式(9)中的"可取常数6.8;当
k呈直线变化。χ系数按受压翼缘扭转有无约束分别取1.4和1.0。
4.3.6
为使梁的整体受力不致产生人为的侧向偏心,加劲肋最好两侧成对配置。但考虑到有些构件不得不在腹板一侧配置横向加劲肋的情况(见图7),故本条增加了一侧配置横向加劲肋的规定。其外伸宽度应大于按公式(4.3.6-1)算得值的1.2倍,厚度应大于其外伸宽度的1/15。其理由如下:
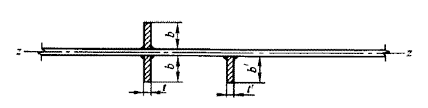
图 7 横向加劲肋的配置方式
钢板横向加劲肋成对配置时,其对腹板水平轴(z—z轴)的惯性矩lz为:
一侧配置时,其惯性矩为:
两者的线刚度相等,才能使加劲效果相同。即:
则:
纵向加劲肋截面对腹板竖直轴线的惯性矩,本规范规定了分界线当
时,用公式(4.3.6-4a)计算;当
时,用公式(4.3.6-4h)计算。
对短加劲肋外伸宽度及其厚度均提出规定,其根据是要求短加劲肋的线刚度等于横向加劲肋的线刚度。即:
取
,
,
得
故规定短加劲肋外伸宽度为横向加劲肋外伸宽度的0.7~1.0倍。
本条还规定了短加劲肋最小间距为0.75h1,这是根据、
、
等常用边长之比的情况导出的。
4.3.8
明确受压翼缘外伸宽厚比分为两档,以便和4.1.1相配合。