5  轴心受力构件和拉弯压弯构件的计算

  5.1 轴心受力构件

5.1.1

本条为轴心受力构件的强度计算要求。

从轴心受拉构件的承载能力极限状态来看，可分为两种情况：

1. 毛截面的平均应力达到材料的屈服强度，构件将产生很大的变形，即达到不适于继续承载的变形的极限状态，其计算式为：

                                      (10)

式中   

：抗力分项系数：对Q235钢， =1.087；对Q345、Q390和Q420钢， =1.111

2. 净截面的平均应力达到材料的抗拉强度fu，即达到最大承载能力的极限状态，其计算式为：

      (11)

由于净截面的孔眼附近应力集中较大，容易首先出现裂缝，因此其抗力分项系数应予提高。上式中参考国外资料取即比增大25%。

本规范为了简化计算，采用了净截面处应力不超过屈服强度的计算方法［即规范中公式（5.1.1-1）］：

        (12)

对本规范推荐的Q235、Q345、Q390钢来说，其屈强比均小于或很接近于0.8，因此一般是偏于安全的。如果今后采用了屈强比更大的钢材，宜用公式（10）和公式（11）来计算，以确保安全。

摩擦型高强度螺栓连接处，构件的强度计算公式是从连接的传力特点建立的。规范中的公式（5.1.1-2）为计算由螺栓孔削弱的截面（最外列螺栓处），在该截面上考虑了内力的一部分已由摩擦力在孔前传走。公式中的系数0.5即为孔前传力系数。根据试验，孔前传力系数大多数情况可取为0.6，少数情况为0.5。为了安全可靠，本规范取0.5。

在某些情况下，构件强度可能由毛截面应力控制，所以要求同时按公式（5.1.1-3）计算毛截面强度。

5.1.2

本条为轴心受压构件的稳定性计算要求。

1. 轴心受压构件的稳定系数，是按柱的最大强度理论用数值方法算出大量-曲线（柱子曲线）归纳确定的。进行理论计算时，考虑了截面的不同形式和尺寸，不同

的加工条件及相应的残余应力图式，并考虑了1/1000杆长的初弯曲。在制定GBJ 17-88根据大量数据和曲线，选择其中常用的96条曲线作为确定值的依据。由于这96条曲线的分布较为离散，若用一条曲线来代表这些曲线，显然不合理，所以进行了分类，把承载能力相近的截面及其弯曲失稳对应轴合为一类，归纳为a、b、c三类。每类中柱子曲线的平均值（即50%分位值）作为代表曲线。

关于轴心压杆的计算理论和算出的各曲线值，参见李开禧、肖允徽等写的”r;逆算单元长度法计算单轴失稳时钢压杆的临界力”和”r;钢压杆的柱子曲线”两篇文章（分别载于《重庆建筑工程学院学报》，1982年4期和1985年2期）。

由于当时计算的柱子曲线都是针对组成板件厚度t＜40mm的截面进行的，规范表5.1.2-1的截面分类表就是按上述依据略加调整确定的。

2. 组成板件t≥40mm的构件，残余应力不但沿板宽度方向变化，在厚度方向的变化也比较显著。板件外表面往往以残余压应力为主，对构件稳定的影响较大。在制定原规范时对此研究不够，只提出了”r;板件厚度大于40mm的焊接实腹截面属c类截面”。后经西安建筑科技大学等单位研究，对组成板件t≥40mm的工字形、H形截面和箱形截面的类别作了专门规定，并增加了d类截面的φ值。在表5.1.2-2中提出的组成板件厚度t≥40mm的轧制H形截面的截面类别，实际上我国目前尚未生产这种型钢，这是指进口钢材而言。

我国的《高层建筑钢结构设计与施工规程》GJG99-98和上海市的同类规程都已经在研究工作的基础上制订了这类稳定系数。前者计算了四种焊接H形厚壁截面的稳定系数曲线，并取一条中间偏低的曲线作为!类系数。后者计算了三种截面的稳定系数曲线，并取其平均值作为d类系数。两者所取截面只有一种是共同的，因而两曲线有些差别，不过在常用的长细比范围内差别不大。基于这一情况，综合两条d曲线取一条新的曲线，其φ值的比较见表7。

表7  

※注：

为正则化长细比（通用长细比），，λ为构件长细比。

为正则化长细比（通用长细比），，为构件长细比。

3.

单轴对称截面绕对称轴的稳定性是弯扭失稳问题。原规范认为对等边单角钢截面、双角钢T形截面和翼缘宽度不等的工字形截面绕对称轴（y轴）的弯扭失稳承载力比弯曲失稳承载力低得不多，值未超出所属类别的范围。仅轧制T形、两板焊接T形以及槽形截面绕对称轴弯扭屈曲承载力较低，降低为c类截面而未计及弯扭。以上处理弯扭失稳问题的办法，难免粗糙，尤其是将”r;无任何对称轴的截面绕任意轴”都按c类截面弯曲屈曲对待更缺少依据。故本规范表5.1.2的截面类别只根据截面形式和残余应力的影响来划分，将弯扭屈曲用换算长细比的方法换算为弯曲屈曲。虽然换算是按弹性进行，但由于弯曲屈曲的φ值考虑了非弹性和初始缺陷，这就相当于弯扭屈曲也间接考虑了非弹性和初始缺陷。

根据弹性稳定理论，单轴对称截面绕对称轴（y轴）的弯扭屈曲临界力和弯曲屈曲临界力及扭转屈曲临界力之间的关系由下式表达：

      (13)

      (14)

式中   

：截面剪心在对称轴上的坐标；

、：构件截面抗扭惯性矩和扇性惯性矩；

：对于剪心的极回转半径；

：-扭转屈曲的计算长度

令   代入公式（13）可得：

              （15）

上式即为规范公式（5.1.2-3）。而式中

对T形截面（轧制、双板焊接、双角钢组合）、十字形截面和角形截面可近似取，因而这些截面的：

           (16)

为了方便计算，对单角钢和双角钢组合T形截面给出简化公式。简化过程中，对截面特性如回转半径和剪心坐标都采用平均近似值。例如等边单角钢对两个主轴的回转半径分别取0.385b和0.195b，剪心坐标取b/3；另外取 双角钢组合T形截面连有填板，其抗扭性能有较大提高。图9所示的等边角钢组合截面，无填板部分（图9a）的抗扭惯性矩为：

有填板部分（图9b），设合并肢与填板的总厚度为2.75t，抗扭惯性矩为：

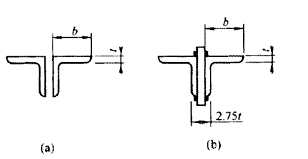
 图 9 双角钢组合T形截面

设有填板（和节点板）部分占杆件总长度的15%，则杆件综合抗扭惯性矩可取：

不等边双角钢组合T形截面也可用类似方法进行计算，推导所得的换算长细比的实用公式均为简单的线性公式。例如等边双角钢截面的实用公式有如下两个：

当时：

当 时：            

其他的双角钢组合T形截面和等边单角钢截面都可按此方法得到简单实用计算式。

4. 对双轴对称的十字形截面构件（图10），其扭转屈曲换算长细比为按公式（16）得：

因此规定”r; 或取值不得小于”，以避免发生扭转屈曲。

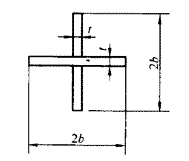
图 10 双轴对称十字形截面

 5. 根据构件的类别和长细比λ（或换算长细比）即可按规范附录8的各表查出稳定系数φ，表中的根号为考虑不同钢种对长细比λ的修正。

为了便于使用电算，采用非线性函数的最小二乘法将各类截面的理论φ值拟合为Perry公式形式的表达式：

当正则化长细比时：

式中

、: 系数，根据截面类别按附录C表C-5取用。

当时（相当于），Perry公式不再适用，采用一条近似曲线使与（）衔接，即对a、b、c、d类截面，系数 a1 值分别为0.41、0.65、0.73和1.35经可靠度分析，采用多条柱子曲线，在常用的λ值范围内，可靠指标基本上保持均匀分布，符合《建筑结构可靠度设计统一标准》GB 50068的要求。

图11为采用的柱子曲线与我国的试验值的比较情况。由于试件的厚度较小，试验值一般偏高，如果试件的厚度较大，有组成板件超过40mm的试件，自然就会有接近于d曲线的试验点。

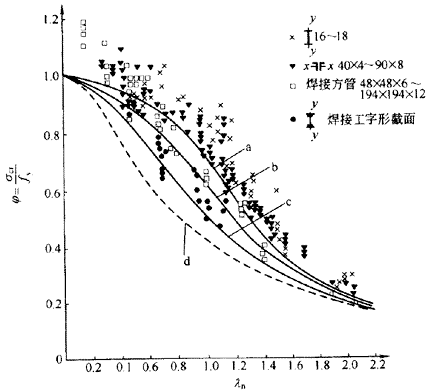
图 11 柱子曲线与实验值

5.1.3

对实腹构件，剪力对弹性屈曲的影响很小，一般不予考虑。但是格构式轴心受压构件，当绕虚轴弯曲时，剪切变形较大，对弯曲屈曲临界力有较大影响，因此计算时应采用换算长细比来考虑此不利影响。

换算长细比的计算公式是按弹性稳定的理论公式，经简化而得：

1. 双肢缀板组合构件，对虚轴的临界力可按下式计算：

即换算长细比为：

                        （18）

式中

：缀板间的距离；

：构件两分肢的轴线距离；

：分肢截面对其弱轴的惯性矩；

：两侧缀板截面惯性矩之和；

：分肢的线刚度；

：两侧缀板线刚度之和。

根据本规范第8.4.1条的规定，。将代入公式（18）中，得：

       （19）

2. 双肢缀条组合构件，对虚轴的临界力可按下式计算：

           (20)

即换算长细比为：

式中  

：斜缀线与构件轴线间的夹角；

：一个节间内两侧斜缀条截面积之和。

本规范条文注2中规定为：α角应在40°～70°范围内。在此范围时，公式（21）中：

       (22)

因此双肢缀条组合构件对虚轴的换算长细比取为：

        (23)

当α角不在40°～70°范围，尤其是小于40°时，上式中的系数值将大于27的甚多，公式（23）是偏于不安全的，此种情况的换算长细比应改用公式（21）计算。

3. 四肢缀板组合构件换算长细比的推导方法与双肢构件类似。一般说来，四肢构件截面总的刚度比双肢的差，构件截面形状保持不变的假定不一定能完全做到，而且分肢的受力也较不均匀，因此换算长细比宜取值偏大一些。根据分析，按角钢的截面最小回转半径计算，可以保证安全。

4. 对四肢缀条组合构件，考虑构件截面总刚度差、四肢受力不均匀等影响，将双肢缀条组合构件中的系数27提高到40。

5. 三肢缀条组合构件的换算长细比是参照国家现行标准《冷弯薄壁型钢结构技术规范》GB 50018的规定采用的。

5.1.4

对格构式受压构件的分肢长细比的要求，主要是为了不使分肢先于构件整体失去承载能力。

对缀条组合的轴心受压构件，由于初弯曲等缺陷的影响，构件受力时呈弯曲状态，使两分肢的内力不等。条文中规定是在考虑构件几何和力学缺陷（总的等效初弯曲取构件长度1/500）的条件下，经计算分析而得的。满足此要求时，可不计算分肢的稳定性。

如果缀条组合的轴心受压构件的，就需要对分肢进行计算，但计算时应计入上述缺陷的影响。

对缀板组合的轴心受压构件，与缀条组合的构件类似，在一定的等效初弯曲条件下，经计算分析认为，当和时，基本上可使分肢不先于整体构件失去承载能力。

5.1.5

双角钢或双槽钢构件的填板间距规定为：对于受压构件是为了保证一个角钢或一个槽钢的稳定；对于受拉构件是为了保证两个角钢和两个槽钢共同工作并受力均匀。由于此种构件两分肢的距离很小，填板的刚度很大，根据我国多年的使用经验，满足本条要求的构件可按实腹构件进行计算，不必对虚轴采用换算长细比。

5.1.6

轴心受压构件的剪力V，分析时取构件弯曲后为正弦曲线（图12）。

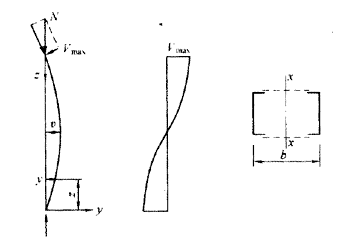
图 12 剪力V计算

设：

    (24)

则：

         (25)

按边缘屈服准则：

        (26)

令、，代入公式（26） 可得:

         (27)

将此v值代入公式（25）中，并使，，得：

       （28）     

        （29）

下标符号见桩基规范中第2.2节，上标暂定用^表示，如平方米用mm^2

对格构柱，稳定系数φ应根据边缘屈服准则求出，或近似地按换算长细比由规范b类截面的表查得。

计算证明，在常用的长细比范围，α值的变化不大，可取定值，即取：

Q235钢     α=85

Q345钢     α=70

Q390钢     α=65

Q420钢     α=62

这些数值恰好与较为吻合，因此建议轴心受压构件剪力的表达式为：

   （30）

为了便于计算，令公式（30）中的，即得规范的公式（5.1.6）：

    （31）

对格构式构件，此剪力由两侧缀材面平均分担，其中三肢柱缀材分担的剪力还应除以cosθ（θ角见本规范图5.1.3）。

实腹式构件中，翼缘与腹板的连接，有必要时可按此剪力进行计算。

5.1.7

重新规定了减小受压构件自由长度的支撑力，不再借用受压构件的偶然剪力。

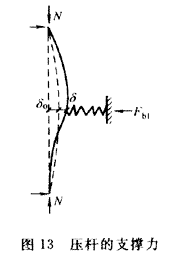
1. 当压杆的长度中点设置一道支撑时（图13），设压杆有初弯曲，受压力后增至，增加的挠度

应等于支撑杆的轴向变形。根据变形协调关系即可得支撑力（参见陈绍蕃《钢结构设计原理》第二版，科学出版社）。当压杆长度中点有一道支撑时，支撑力，与原规范规定的偶然剪力相比，当压杆长细比（对Q235钢）或,&（对Q345钢）时，小于偶然剪力。

2. 当一道支撑支于距柱端al时，则支撑力。当α=0.4时，

与N/60相比仅相差4%。因此对不等间距支承，若间距与平均间距相比相差不超过20%时，可认为是等间距支承。

3. 支承多根柱的支撑力取为，式中n为被撑柱的根数，ΣNi为被撑柱同时存在的轴心压力设计值之和。

支撑多根柱的支撑，往往承受较大的支撑力，因此不能再只按容许长细比选择截面，需要按支撑力进行计算，且一道支撑架在一个方向所撑柱数不宜超过8根。

4. 本条中还明确提出下列两项：

1)  支撑力可不与其他作用产生的轴力叠加，取两者中的较大值进行计算。

2) 支撑轴线应通过被撑构件截面的剪心［对双轴对称截面，剪心与形心重合；对单轴对称的T形截面（包括双角钢组合T形）及角形截面，剪心在两组成板件轴线相交点，其他单轴对称和无对称轴截面剪心位置可参阅有关力学或稳定理论资料］。