7.4 梁与柱的刚性连接 

本节为新增内容。

7.4.1

梁与柱刚性连接时，如不设置柱腹板的横向加劲肋，对柱腹板和翼缘厚度的要求是：

1. 在梁受压翼缘处，柱腹板的厚度应满足强度和局部稳定的要求。公式（7.4.1-1）是根据梁受压翼缘与柱腹板在有效宽度范围内等强的条件来计算柱腹板所需的厚度。计算时忽略了柱腹板向轴向（竖向）内力的影响，因为在主框架节点内，框架梁的支座反力主要通过柱翼缘传递，而连于柱腹板上的纵向梁的支座反力一般较小，可忽略不计。日本和美国均不考虑柱腹板竖向应力的影响。

公式（7.4.1-2）是根据柱腹板在梁受压翼缘集中力作用下的局部稳定条件，偏安全地采用的柱腹板宽厚比的限值。

2. 柱翼缘板按强度计算所需的厚度可用规范公式（7.4.1-3）表示，此式源于AISC，其他各国亦沿用之。现简要推演如下（图22）：

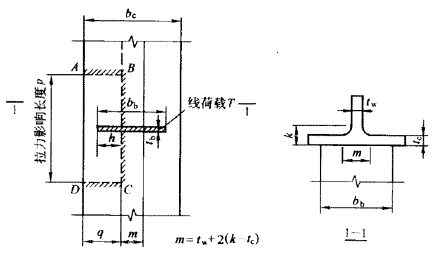
图 22 柱翼缘在拉力下的受力情况

在梁受拉翼缘处，柱翼缘板受到梁翼缘传来的拉力（为梁受拉翼缘截面积，为梁钢材抗拉强度设计值）。T由柱翼缘板的三个组成部分承担，中间部分（分布长度为m）直接传给柱腹板的力为，其余各由两侧ABCD部分的板件承担。根据试验研究，拉力在柱翼板上的影响长度p≈12tc，并可将此受力部分视为三边固定一边自由的板件，在固定边将因受弯而形成塑性铰。因此可用屈服线理论导出此板的承载力设计值为，式中C1为系数，与几何尺寸p、h、q等有关。对实际工程中常用的宽翼缘梁和柱，，可偏安全地取。这样，柱翼缘板受拉时的总承载力为：考虑到冀板中间和两侧部分的抗拉刚度不同，难以充分发挥共同工作，可乘以0.8的折减系数后再与拉力T相平衡：

在上式中，愈小，愈大。按统计分析， 的最小值约为0.15，以此代入，即得，即。

7.4.2

当梁柱刚性连接处不满足本规范7.4.1条的要求时，应设置柱腹板的横向加劲肋。在以柱翼缘和横向加劲肋为边界的节点腹板域，所受的剪力为（图23）：

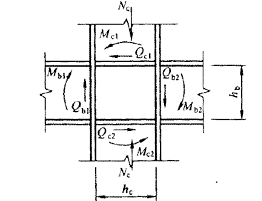
图 23 节点腹板域受力状态

剪应力应满足：

实际上节点腹板域的周边有柱翼缘和加劲肋提供的约束，使抗剪承载力大大提高。试验证明可将节点域的抗剪强度提高到。另外，在节点域设计中弯矩的影响最大，当略去式中剪力项的有利影响，则求得的剪应力τ偏于安全且使算式简化，因此上式即成为：

式中

tw为柱腹板厚度，令，为节点腹板域的体积；

对箱形截面柱，考虑两腹板受力不均的影响，取。

在上述节点板域的抗剪强度计算中同样没有考虑柱腹板轴力的影响，这是因为抗剪强度提高到后仍留有较大的余地，而且略去剪力项后使算得的剪应力偏高20%～30%，而柱腹板的轴压力对抗剪强度的影响系数为（N为柱腹板轴压力设计值，为柱腹板的屈服轴压承载力）。当影响系数为0.83～0.77（相当于略去剪力项后使剪应力计算值增加20%～30%）时，而框架节点以承受弯矩为主，只要柱截面在、作用下产生拉应力，将小于0.5，可以忽略。

节点腹板域除应按式（7.4.2-1）验算强度外，还应接式（7.4.2-2）验算局部稳定，式（7.4.2-2）与现行国家标准《建筑抗震设计规范》GB 50011 对高层钢结构的规定相同，采用了美国的建议，是在强震作用下不产生弹塑性剪切失稳的条件。但我国的初步研究则认为在轴力与剪力共同作用下保证不失稳的条件应为。考虑到在抗震规范中对高层钢结构因柱截面尺寸较大已采用了公式（7.4.2-2），为与其协调，并将其作为最低限值，故本规范亦采用式（7.4.2-2）。

当柱腹板节点域不满足公式（7.4.2-1）的要求时，应采取加强措施。其中加贴补强板的措施有两种，在国外均有应用实例。至于斜向加劲肋则主要用于轻型结构，因它对抗震耗能不利，而且与纵向梁连接时构造上亦有困难。