7.5 连接节点处板件的计算  

本节为新增内容。

7.5.1

连接节点处板件在拉、剪共同作用下的强度计算公式是根据我国对双角钢杆件桁架节点板的试验研究中拟合出来的，它同样适用于连接节点处的其他板件，如规范中图7.5.1。

我们试验的桁架节点板大多数是弦杆和腹杆均为双角钢的K形节点，仅少数是竖杆为工字钢的N形节点。抗拉试验共有6种不同形式的16个试件。所有试件的破坏特征均为沿最危险的线段撕裂破坏，即图24中的三折线撕裂，其中、与节点板的边界线基本垂直。

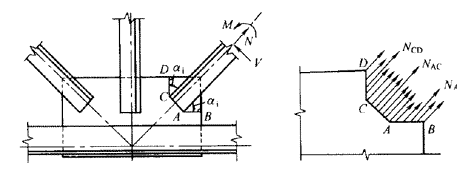
图 24 节点板受拉计算简图

规范公式（7.5.1）的推导过程如下：

在图24中，沿BACD撕裂线割取自由体，由于板内塑性区的发展引起的应力重分布，假定在破坏时撕裂面上各线段的应力在线段内均匀分布且平行于腹杆轴力，当各撕裂段上的折算应力同时达到抗拉强度时，试件破坏。根据平衡条件并忽略很小的M和V，则：

式中

： 第撕裂段的长度，为节点板厚度。

设为第段撕裂线与腹杆轴线的夹角，则第i段撕裂面上的平均正应力和平均剪应力为：

令则：

按极限状态设计法，即：

式中

：节点板钢材的强度设计值；

：斜腹杆的轴向内力设计值；

：为第段撕裂面的净截面积。

公式（70）符合破坏机理，其计算值与试验值之比平均为87.5%，略偏于安全且离散性较小。

7.5.2

考虑到桁架节点板的外形往往不规则，用规范公式（7.5.1）计算比较麻烦，加之一些受动力荷载的桁架需要计算节点板的疲劳时，该公式更不适用，故参照国外多数国家的经验，建议对桁架节点板可采用有效宽度法进行承载力计算。所谓有效宽度即认为腹杆轴力N将通过连接件在节点板内按照某一个应力扩散角度传至连接件端部与N相垂直的一定宽度范围内，该一定宽度即称为有效宽度。

在试验研究中，假定范围内的节点板应力达到，并令（为节点板破坏时的腹杆轴力），按此法拟合的结果：当应力扩散角θ=27°时精确度最高，计算值与试验值的比值平均为98.9%；当θ=30°时此比值为106.8%。考虑到国外多数国家对应力扩散角均取30°，为与国际接轨且误差较小，故亦建议取θ=30°。

有效宽度法计算简单，概念清楚，适用于腹杆与节点板的多种连接情况，如侧焊、围焊和铆钉、螺栓连接等（当采用铆钉或螺栓连接时应取为有效净宽度）。

当桁架弦杆或腹杆为:形钢或双板焊接T形截面时，节点构造方式有所不同，节点内的应力状态更加复杂，故规范公式（7.5.1）和（7.5.2）均不适用。

用有效宽度法可以制作腹杯内力N与节点板厚度t的关系表，我们先制作了表，反映了影响有效宽度的斜腹杆连接肢宽度b和侧焊缝焊脚尺寸地、的作用，因而该表比以往的表更精确。但由于表形较复杂且参数b和hf的可变性较大，使用不便。为方便设计，便在表的基础上按不同参数组合下的最不利情况整理出包络图表（表10），使该表具有较充分的依据，而且在常用不同参数、下亦是安全的。

表10  

※注：

1. 本表的适用范围为：

1）适用于焊接桁架的节点板强度验算，节点板钢材为Q235，焊条E43；

2）节点板边缘与腹杆轴线之间的夹角应不小于30°；

3）节点板与腹杆用侧焊缝链接，当采用围焊时，节点板的厚度应通过计算确定；

4）对有竖腹杆的节点板，当时，可不验算节点板的稳定；对无竖腹杆的节点板，当时，可将受压腹杆的内力诚意增大系数1.25后再查求节点板厚度，

此时亦可不验算节点板的稳定；式中c为受压腹杆链接肢端面中点沿腹杆轴线方向至弦杆的净距离。

2.  支座节点板的厚度宜较中间节点板增加2mm。

7.5.3

本条为桁架节点板的稳定计算要求。

1. 共作了8个节点板在受压斜腹杆作用下的试验，其中有无竖腹杆的各4个试件。试验表明：

1） 当节点板自由边长度与其厚度之比时，节点板的稳定性很差，将很快失稳，故此时应沿自由边加劲。

2） 有竖腹杆的节点板或的无竖腹杆节点板在斜腹杆压力作用下，失稳均呈三折线屈折破坏，其屈折线的位置和方向，均与受拉时的撕裂线类同。

3） 节点板的抗压性能取决于的大小（为受压斜腹杆连接肢端面中点沿腹杆轴线方向至弦杆的净距，t为节点板厚度），在一般情况下，愈大，稳定承载力愈低。

 ① 对有竖腹杆的节点板，当时，节点板的抗压极限承载力与抗拉极限承载力大致相等，破坏的安全度相同，故此时可不进行稳定验算。当时，，应按本规范附录F的近似法验算稳定；当时，近似法算出的计算值将大于试验值，不安全，故规。

 ② 对无竖腹杆的节点板，，故一般都应该验算稳定，当时，节点板用近似法的计算值将大于试验值，不安全，故规定。

4） 的无竖腹杆节点板沿自由边加劲后，在受压斜腹杆作用下，节点板呈两折线屈折，这是由于区因加劲加强后，稳定承载力有较大提高所致。但此时，故仍需验算稳定，不过，仅需验算区和区而不必验算区而已。

2. 本规范附录F所列桁架节点板在斜腹杆轴压力作用下的稳定计算公式是根据8个试件的试验结果拟合出来的。根据破坏特征，节点板失稳时的屈折线主要是三折线形（见本规范附录F图F.0.1）。为计算方便且与实际情况基本相符，假定平行于弦杆，。

从试验可知，在斜腹杆轴压力N作用下，节点板内存在三个受压区，即区（FBGHA板件）、区（AIJC板件）和区（CKMP板件）。当其中某一个受压区先失稳后，其他各区立即相继失稳，因此有必要对三个区分别进行验算。其中区往往起控制作用。

计算时要先将腹杆轴压力N分解为三个平行分力各自作用于三个受压区屈折线的中点。平行分力的分配比例假定为各屈折线段在有效宽度线（在本规范附录F图F.0.1中为的延长线）上投影长度与的比值。然后再将此平行分力分解为垂直于各屈折线的力，应小于或等于各受压区板件的稳定承载力。而受压区板件则可假定为宽度等于屈折线长度的钢板，按轴压构件计算其稳定承载力。钢板长度取为板件的中线长度，计算长度系数经拟合后取为0.8，长细比。这样各受压板区稳定验算的表达式为：

区：

区:

区：

其中、、分别为各区屈折线、、的长度；

、、为各屈折线在有效宽度线上的投影长度；

t为板厚；为各受压板区的轴压稳定系数，按计算。

对且沿自由边加劲的无竖腹杆节点板失稳时，一般呈两屈折线屈曲，显然，在区因加劲后其稳定承载力大为提高，已不起控制作用，故只需用上述方法验算区和区的稳定。

用上述拟合的近似法计算稳定的结果表明，试件的极限承载力计算值与试验值之比平均为85%，计算值偏于安全。

3. 为了尽量缩小稳定计算的范围，对于无竖腹杆的节点板，我们利用国家标准图梯形钢屋架（G511）和钢托架（G513）中的16个节点，用同一根斜腹杆对节点板作稳定和强度计算，并进行对比以达到用强度计算的方法来代替稳定计算的目的。

对比结果表明：当10。大多数节点的大于（、为节点板的稳定和强度计算承载力），仅少数节点的，此时的斜腹杆倾角θ1大多接近60°，这说明θ1的大小对稳定承载力的影响较大。

因为强度计算时的有效宽度，而稳定计算中假定斜腹杆轴压力N分配的有效宽度（式中、为斜腹杆两侧角焊缝的长度）当θ1=60°或30°时，，与相差最大，此时的稳定计算承载力亦最低。

设，经统计，k≈0.356，因此，当θ1=60°或30°时的、值分别为：

本规范附录F公式（F.0.2-2），

当时，,（Q235钢）和0.910（Q420钢），这样，稳定承载力计算值与受拉计算抗力之比为：

，平均为0.784

因此，对无竖腹杆的节点板，当且时，可将按强度计算［公式（70）］的节点板抗力乘以折减系数0.784作为稳定承载力。考虑到稳定计算公式偏安全近15%，故可将折减系数取为0.8（0.8/0.784=1.020），以方便计算。

当然，必要时亦可专门进行稳定计算，若时,则应按近似公式计算稳定。