10.3 杆件和节点承载力

10.3.2

根据本规范第10.2.5条的规定，支管与主管连接焊缝可沿全周采用角焊缝，也可部分采用对接焊缝。由于坡口角度、焊根间隙都是变化的，对接焊缝的焊根又不能清渣及补焊，考虑到这些原因及方便计算，故参考国外规范的规定，连接焊缝计算时可视为全周角焊缝按本规范公式（7.1.3-1）计算，取。

焊缝的长度实际上是支管与主管相交线长度，考虑到焊缝传力时的不均匀性，焊缝的计算长度均不大于相交线长度。因主、支管均为圆管的节点焊缝传力较为均匀，焊缝的计算长度取为相交线长度，该相交线是一条空间曲线。若将曲线分为2n段，微小段可取空间折线代替空间曲线。则焊缝的计算长度为：

          (73)

式中

:相交线率。它是和的函数，即：

经采用回归分析方法，提出了规范中的公式（10.3.2-1）和公式（10.3.2-2）。两式精度较高，计算也较方便。

圆管节点焊缝有效厚度沿相交线是变化的。第区段的焊缝有效厚度为：

          (74)

式中

：第段中点支管外壁切平面与主管外壁切平面的夹角。

沿焊缝长度有效厚度平均值：

C值与和θ有关，经电算分析，一般C＞0.7，最低为0.6079。C值小于0.7都发生在θ＞60°的情况，考虑到这时支管与主管的连接焊缝基本上属于端焊缝，它的强度将比侧焊缝强度规定值高30%，放取C=0.7是安全的目前国际上对角焊缝的计算考虑外荷载方向，这样经电算分析其有效厚度平均系数C均大于0.7，最高可达0.8321.放取还是合适的。

矩形管书点支管与主管的相交线是直线，计算方便，但考虑到主管顶面板件沿相交线周围在支管轴力作用下刚度的差异和传力的不均匀性，相交焊缝的计算长度将不等于周长，需由试验研究而得。本条公式（10.3.2-3～10.3.2-5）引自《Design Guide ForRectangular Hollow Section （RHS）Joints Under Predominantly Static Loading》Verlag Tǔv Rheinland，1992，P19～20《空心管结构连接设计指南》J.A.Packer，科学出版社，1997年版，第246～249页。该公式是在试验研究基础上归纳出来的，既简单又可靠。

10.3.3

本条为圆管节点的承载力适用范围和要求。

原规范对保证钢管节点处主管强度的支管轴心承载力设计值的公式是比较、分析国外有关规范和国内外有关资料的基础上，根据近300个各类型管节点的承载力极限值试验数据，通过回归分析归纳得出承载力极限值经验公式，然后采用校准法换算得到的。

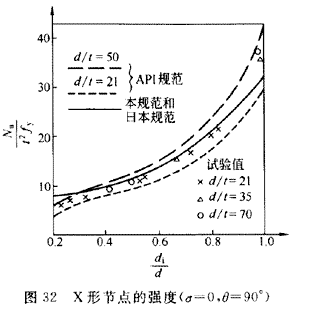
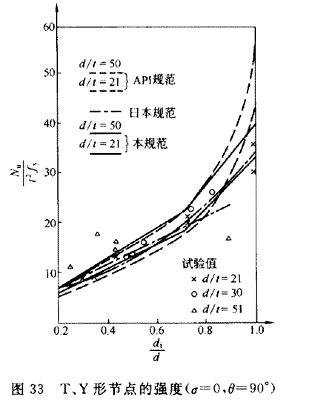
X形和T、Y形节点的承载力极限值与试验值比较见图32、图333。图中纵坐标用无量纲系数表达。图32、图33中也给出了美国石油学会API RP-2A规范和日本《钢管结构设计施工指南》中所采用的计算曲线，以便比较。对于X形节点，从图32可看出d/t对节点强度影响不大，故采用单一曲线公式已有足够的精度。对T、Y形节点，本规范采用折线形公式，并以计及径厚比对节点强度的影响。由图33可见，其计算值与试验结果吻合较好。

K形节点强度的几何影响因素较多，情况也较复杂。一般说来由于两支管受力（拉压）性质不同，限制了节点局部变形，提高了节点强度。API规范和欧洲《钢结构规范》对K形节点公式的计算误差较大，一般偏于保守。本规范对K形节点公式是采用将T、Y形节点强度乘上提高系数得到的。节点强度的提高值体现在中三个代数式的乘积，它分别反映了间隙比a/d、径厚比d/t和直径比的影响。这三个代数式是通过对有关试验资料的回归分析确定的。图34给出了K形节点的计算值和试验值的比较。图中也给出了日本规范的曲线。

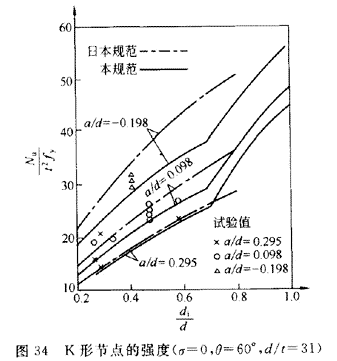
由于K形节点的强度对各种随机因素的敏感性较强，试验值本身的离散性较大，在一般情况下本条公式的取值也略低一些。对于搭接节点，规定仍按a=0计算，稍偏保守。这是考虑到搭接节点相交线几何形状更为复杂，而目前加工、焊接、装配经验不足，另外也是为了进一步简化计算。从与试验值对比的统计计算结果看，这样计算的结果比采用精确而烦琐的公式计算，离散度的增加并不明显，仅2%左右。

除了几何因素影响外，管节点强度与节点受力状态关系很大，如支管与主管的夹角θ、支管受压还是受拉，以及主管轴向应力情况等。

试验表明，支管轴心力垂直于主管方向的分力是造成节点破坏的主要因素。支管倾角θ越小，支管轴心力的垂直分力也越小，节点承载力就越高。由于支管倾斜使相交线加长和支管轴心力的水平分力分别会对节点强度产生有利和不利的影响。但由于其影响相对较小，并相互抵消，为计算方便起见，公式中未予考虑。公式中用来表达支管倾角θ对节点强度的影响，也就是说仅考虑支管轴力垂直分力作用。

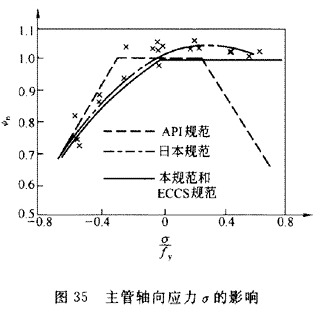
圆管节点的破坏多由于节点处过大的局部变形而引起的。当主管受轴向压应力时，将促使节点的局部变形，节点强度随主管压应力增大而降低，而当主管受轴向拉应力时，可减小节点局部变形，此时节点承载力比主管σ=0时约高3%～4%,如图35 所示.本公式在σ＜0时，采用二次抛物线；而当σ＞0时，为简化计算近似取σ=0时的值，即=1。这样基本与试验结果符合。

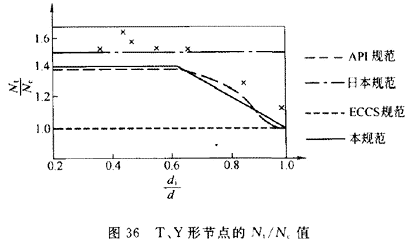
当支管承受压力时，节点的破坏主要是由于主管壁的局部屈曲引起的，而当支管承受拉力时主要是强度破坏。大量试验得出结论4支管受拉时承载力的数据离散性大，大约比受压时大1.4～1.7倍。对X形节点，经分析，用规范公式（10.3.3-2行计算。对T、Y形节点，由图36中的试验点可看出：当β＞0.6时，值由1.4逐步下降，公式中采用直线下降，当β趋近于1.0时，节点的破坏已趋近于强度破坏的性质，无论支管受压还是受拉，其强度差别不大。

原规范在确定圆钢管节点承载力极限值公式时，以经过筛选的日本和欧美大量的试验数据为依据，对日本、欧洲、美国规范中的公式和本规范采用的公式进行了统计分析比较。由统计离散度看，除K形搭接节点外，均较日本、欧洲、美国公式计算精度有所提高或相当，K形搭接节点也接近于日本公式的结果。

这次对圆管节点承载力设计值计算公式的修订工作，是根据同济大学的研究成果进行的。除对平面管节点承载力的计算公式作局部修正外，还增加了空间管节点承载力的计算方法。

随着钢管结构的发展，应用到结构中的钢管书点的尺寸越来越大；由于试件的尺寸效应对节点试验承载力有影响，因此先前节点尺寸过小的试验数据被删除，新的试验数据得到了补充，一个包含1546个圆钢管节点试验结果和790个圆钢管节点有限元分析结果的数据库建立了起来。根据不断补充的试验数据，一些国家和组织如日本和国际管结构研究和发展委员会（CIDECT）从20世纪80年代起，对节点强度计算公式作了不同程度的修改。

对于圆钢管节点强度计算公式的修正是对照新建立的管节点数据库中的试验结果（由于不少试验的破坏模式为支管破坏，分析时只采用属于节点破坏的试验结果），比较了原规范中平面管节点强度公式的计算结果得出的。同时又将GBJ 17-88公式、日本建筑学会（AIJ）公式、国际管结构研究和发展委员会（CIDECT）公式和本规范修订后的公式与试验数据进行了比较后得出来的。其对比结果如表12所示。

表12  

※注：

表中m为规范公式计算值与试验值比值的平均值，σ为方差，v为离散度，cl为置信度。

对修改各点说明如下：

1. 将d/t的取值范围从d/t≤50改为d/t≤100。由于钢管节点试验的尺寸越来越大，d/t值也已超过50，K、T、X形试验节点的d/t都达到100。这一扩大也与本规范第5.4.5条一致。

2. 对于X形节点，支管受压情形下GBJ 17-88 的计算结果置信度和均值皆较适中，且介于AIJ和CIDECT之间，故未作调整；支管受拉情形下GBJ 17-88的计算结果均值偏低，改为式（10.3.3-2）后，均值提高为0.7032，置信度仅微有降低，比修正前更合理。

3. 由于T、Y形节点支管受压情形下GBJ 17-88的计算结果置信度偏低，故将承载力设计值降低5%，即将原规范式中的12.12改为本规范公式（10.3.3-3）中的11.51，修正后的计算结果置信度提高至80.53%，比修正前更合理；相应地，T、Y形节点支管受拉情形下修正后的计算结果置信度提高至78.80%。

4. 由于T、Y形节点是,形节点在间隙a为无穷大时的特例，,形节点受压情形下GBJ 17-88 的计算公式中12.12也相应地改为11.51［见本规范公式（10.3.3.-6）］，修正后的计算结果置信度和均值皆较适中，且介于AIJ和CIDECT之间，因而是可行的。

5. GBJ 17-88 没有空间管节点强度计算公式，而目前国内的空间管结构中已大量出现KK形节点和TT形节点，增加相应的计算公式是必要的。本规范公式（10.3.3-9）、（10.3.3-10）及第#款的规定是对试验结果进行数据分析得出的，这些公式比AIJ和CIDECT的计算公式更为合理。

6. 试验数据中TT形和KK形管节点支管的横向夹角φ分布在60°～120°之间，故将φ限定在该范围内，同时φ确定后支管的横向间距g即已相应地确定。

7. 由于XX形管节点的数据较少，AIJ和CIDECT计算公式的计算结果与试验结果吻合情况也不甚理想，而这种节点类型目前在实际应用中较少用到，故在本规范内未予列入。

8. 在规范公式（10.3.3-1）中，将主管轴力影响系数表达式中对主管轴向应力σ的定义由原来的”r;最大轴向应力（拉应力为正，压应力为负）”改为”r;节点两侧主管轴心压应力的较小绝对值”是为了使用方便，不易混淆，且与国外资料相符。由于采用了绝对值，故将的公式改为： 。

当节点一侧的主管受压另一侧受拉时，可将σ取为零，此时=1.0

10.3.4

矩形管（含方管）平面管节点承载力设计值计算公式，是根据哈尔滨工业大学的研究成果并结合国外资料补充的。

试验研究表明，矩形管节点有7种破坏模式=主管平壁因形成塑性铰线而失效；主管平壁因冲切而破坏或主管侧壁因剪切而破坏；主管侧壁因受拉屈服或受压局部失稳而失效；受拉支管被拉坏；受压支管因局部失稳而失效；主管平壁因局部失稳而失效；有间隙的K、N形节点中，主管在间隙处被剪坏或丧失轴向承载力而破坏等。有时几种失效模式同时发生。国外已针对不同破坏模式给出了节点承载力的计算公式，这些公式只有少数是理论推出的，大部分是经验公式。CIDECT和欧洲规范（Eurocode 3）均采用了这些公式作为节点的承载力设计值公式，没有给出正常使用极限状态的验算公式。

国外的新近研究成果指出，对于以主管平壁形成塑性铰线的破坏模式，应考虑两种极限状态的验算。建议取令主管表面的局部凹（凸）变形达主管宽度b的3%时的支管内力为节点的极限承载力（承载力极限状态）；取局部变形为0.01b的支管内力为节点正常使用极限状态的控制力。至于由哪个极限状态起控制作用，应视承载力极限状态的承载力与正常使用极限状态的控制力的比值K而定。若K值小于折算的总安全系数，则承载力极限状态起控制作用，反之由正常使用极限状态起控制作用。欧洲规范的总安全系数是1.5，因此当K＞1.5时，应验算正常使用状态。分析表明，当β＜0.6、b/t＞15时，一般由正常使用极限状态局部变形（δ=0.16b）控制。目前尚没有简单的变形计算公式可供应用。

根据哈尔滨工业大学的管节点试验和考虑几何和材料非线性的有限元分析结果，以及国内外收集到的其他试验结果，对CIDECT和欧洲规范的公式进行了局部修订，得到了本规范的承载力设计值公式。具体修改如下：

1. 考虑到在以主管平壁形成塑性铰线为破坏模式的某些情况下，节点将由正常使用极限状态控制，为避免复杂的变形验算，将相应公式乘以0.9的系数予以降低，作为节点的极限承载力设计值［即得本规范公式（10.3.4-1）和（10.3.4-6）］。经大量有限元分析表明，采取上述处理方法，可不必再验算节点的正常使用极限状态。

2. 将主管因受轴心压力使节点承载力降低的参数表达式改为：，与国外的相关公式比较，该式没有突变，符合有限元分析和试验结果，并可用于β=1.0的节点。

改为。这一修改符合试验结果的破坏模式，经与收集到的国外49个试验结果和哈尔滨工业大学5个主管截面高宽比h/b≥2的等宽.形节点的有限元分析结果相比，精度远高于国外公式。以屈服应力代入修订后的公式所得结果与试验结果的比值作为统计值，27个试验的平均值为0.830，其方差为0.111，而按国外的公式计算，这两个值分别为0.531和0.195。在本规范修订过程中，还考虑了1.25倍的附加安全系数和主管受压时节点承载力降低的参数，使本规范公式（10.3.4-2）的计算值不致较国外公式提高的太多。

4 对β=1.0的X形节点侧壁抗剪验算的规范公式（10.3.4-3）补充了限制条件：当且时，尚应验算主管侧壁的抗剪承载力。该条件排除了支管壁可能帮助抗剪的情况。

5 矩形管节点其他破坏模式的计算公式均与CIDECT和欧洲规范的相同，仅将国外公式中的用f代替。国外节点承载力设计值的表达式可简写为：

式中

：平均荷载系数，其值约为我国平均荷载系数的1.1倍；

：荷载效应标准值；

：以表述的节点极限承载设计值。

若将公式中的用f乘以抗力分项系数代替，则考虑将上述二式代入公式（75）后，即得本规范的表达通式：

由此可见，除以塑性铰线失效模式控制的承载力公式（10.3.4-1）和（10.3.4-6）以外，国内外管节点的承载力设计值的安全系数大体相当。