6.2.2
框架结构的变形能力与框架的破坏机制密切相关。试验研究表明,梁先屈服,可使整个框架有较大的内力重分布和能量消耗能力,极限层间位移增大,抗震性能较好。
在强震作用下结构构件不存在强度储备,梁端实际达到的弯矩与其受弯承载力是相等的,柱端实际达到的弯矩也与其偏压下的受弯承载力相等。这是地震作用效应的一个特点。因此,所谓”r;强柱弱梁”指的是:节点处梁端实际受弯承载力和柱端实际受弯承载力
之间满足下列不等式:
这种概念设计,由于地震的复杂性、楼板的影响和钢筋屈服强度的超强,难以通过精确的计算真正实现。国外的抗震规范多以设计承载力衡量或将钢筋抗拉强度乘以超强系数。
本规范的规定只在一定程度上减缓柱端的屈服。一般采用增大柱端弯矩设计值的方法。在梁端实配钢筋不超过计算配筋10%的前提下,将承载力不等式转为内力设计值的关系式,不同抗震等级的柱端弯矩设计值有不同程度的差异。
对于一级,89规范除了用增大系数的方法外,还提出了采用梁端实配钢筋面积和材料强度标准值计算的抗震受弯承载力所对应的弯矩值来提高的方法。这里,抗震承载力即本规范5章的RE=R/γRE,此时必须将抗震承载力验算公式取等号转换为对应的内力,即S=R/γRE。当计算梁端抗震承载力时,若计入楼板的钢筋,且材料强度标准值考虑一定的超强系数,则可提高框架结构”r;强柱弱梁”的程度。89规范规定,一级的增大系数可根据工程经验估计节点左右梁端顺时针或反时针方向受拉钢筋的实际截面面积与计算面积的比值λs,取1.1λs,作为弯矩增大系数ηc的近似估计。其值可参考λs的可能变化范围确定。
本次修订提高了强柱弱梁的弯矩增大系数ηc,9度时及一级框架结构仍考虑框架梁的实际受弯承载力;其他情况,弯矩增大系数ηc考虑了一定的超配钢筋和钢筋超强。
当框架底部若干层的柱反弯点不在楼层内时,说明该若干层的框架梁相对较弱,为避免在竖向荷载和地震共同作用下变形集中,压屈失稳,柱端弯矩也应乘以增大系数。
对于轴压比小于0.15的柱,包括顶层柱在内,因其具有与梁相近的变形能力,可不满足上述要求;对框支柱,在第6.2.10条另有规定,此处不予重复。
由于地震是往复作用,两个方向的弯矩设计值均要满足要求。当柱子考虑顺时针方向之和时,梁考虑反时针方向之和;反之亦然。
6.2.3
框架结构的底层柱底过早出现塑性屈服,将影响整个结构的变形能力。底层柱下端乘以弯矩增大系数是为了避免框架结构柱脚过早屈服。对框架-抗震墙结构的框架,其主要抗侧力构件为抗震墙,对其框架部分的底层柱底,可不作要求。
6.2.4、6.2.5、6.2.8
防止梁、柱和抗震墙底部在弯曲屈服前出现剪切破坏是抗震概念设计的要求,它意味着构件的受剪承载力要大于构件弯曲时实际达到的剪力,即按实际配筋面积和材料强度标准值计算的承载力之间满足下列不等式:
规范在超配钢筋不超过计算配筋10%的前提下,将承载力不等式转为内力设计表达式,仍采用不同的剪力增大系数,使”r;强剪弱弯”的程度有所差别。该系数同样考虑了材料实际强度和钢筋实际面积这两个因素的影响,对柱和墙还考虑了轴向力的影响,并简化计算。
一级的剪力增大系数,需从上述不等式中导出。直接取实配钢筋面积Aas与计算实配筋面积Acs之比λs的1.1倍,是ηv最简单的近似,对梁和节点的”r;强剪”能满足工程的要求,对柱和墙偏于保守。89规范在条文说明中给出较为复杂的近似计算公式如下:
式中,λN为轴压比,λsw为墙体实际受拉钢筋(分布筋和集中筋)截面面积与计算面积之比,ζ为考虑墙体边缘构件影响的系数, ρtw为墙体受拉钢筋配筋率。
当柱λs≤1.8、λN≥0.2且ρt=0.5%~2.5%,墙λsw≤1.8、λN≤0.3且ρtw=0.4%~1.2%时,通过数百个算例的统计分析,能满足工程要求的剪力增大系数ηv的进一步简化计算公式如下:
本次修订,框架柱、抗震墙的剪力增大系数ηvc、ηvw,即参考上述近似公式确定。
注意:柱和抗震墙的弯矩设计值系经本节有关规定调整后的取值;梁端、柱端弯矩设计值之和须取顺时针方向之和以及反时针方向之和两者的较大值;梁端纵向受拉钢筋也按顺时针及反时针方向考虑。
6.2.7
对一级抗震墙规定调整各截面的组合弯矩设计值,目的是通过配筋方式迫使塑性铰区位于墙肢的底部加强部位。89规范要求底部加强部位以上的组合弯矩设计值按线性变化,对于较高的房屋,会导致弯矩取值过大。为简化设计,本次修订改为:底部加强部位的弯矩设计值均取墙底部截面的组合弯矩设计值,底部加强部位以上,均采用各墙肢截面的组合弯矩设计值乘以增大系数。
底部加强部位的纵向钢筋宜延伸到相邻上层的顶板处,以满足锚固要求并保证加强部位以上墙肢截面的受弯承载力不低于加强部位顶截面的受弯承载力。
双肢抗震墙的某个墙肢一旦出现全截面受拉开裂,则其刚度退化严重,大部分地震作用将转移到受压墙肢,因此,受压肢需适当增加弯矩和剪力。注意到地震是往复的作用,实际上双肢墙的每个墙肢,都可能要按增大后的内力配筋。
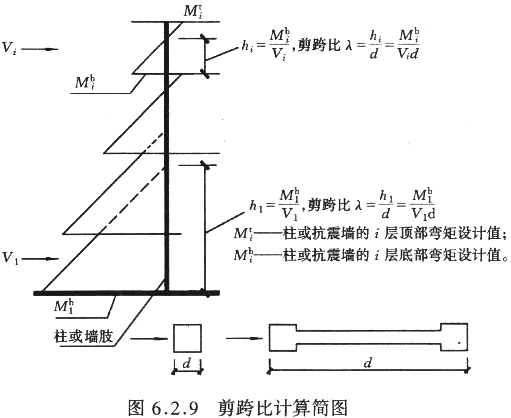
6.2.9
框架柱和抗震墙的剪跨比可按图6.2.9及公式进行计算。
6.2.11
框支结构落地墙,在转换层以下的部位是保证框支结构抗震性能的关键部位,这部位的剪力传递还存在矮墙效应。为了保证抗震墙在大震时的受剪承载力,只考虑有拉筋约束部分的混凝土受剪承载力。
无地下室的单层框支结构的落地墙,特别是联肢或双肢墙,当考虑不利荷载组合出现偏心受拉时,为了防止墙与基础交接处产生滑移,除满足本规范(6.2.14)公式的要求外,宜按总剪力的30%设置45°交叉防滑斜筋,斜筋可按单排设在墙截面中部并应满足锚固要求。
6.2.13
本条规定了在结构整体分析中的内力调整:
1. 框架-抗震墙结构在强烈地震中,墙体开裂而刚度退化,引起框架和抗震墙之间塑性内力重分布,需调整框架部分承担的地震剪力。调整后,框架部分各层的剪力设计值均相同。其取值既体现了多道抗震设防的原则,又考虑了当前的经济条件。
此项规定不适用于部分框架柱不到顶,使上部框架柱数量较少的楼层。
2. 抗震墙连梁内力由风荷载控制时,连梁刚度不宜折减。地震作用控制时,抗震墙的连梁考虑刚度折减后,如部分连梁尚不能满足剪压比限值,可按剪压比要求降低连梁剪力设计值及弯矩,并相应调整抗震墙的墙肢内力。
3. 对翼墙有效宽度,89规范规定不大于抗震墙总高度的1/10,这一规定低估了有效长度,特别是对于较低房屋,本次修订,参考UBC97的有关规定,改为抗震墙总高度的15%。
6.2.14
抗震墙的水平施工缝处,由于混凝土结合不良,可能形成抗震薄弱部位。故规定一级抗震墙要进行水平施工缝处的受剪承载力验算。
验算公式依据于试验资料,忽略了混凝土的作用,但考虑轴向压力的摩擦作用和轴向拉力的不利影响。穿过施工缝处的钢筋处于复合受力状态,其强度采用0.6的折减系数。还需注意,在轴向力设计值计算中,重力荷载的分项系数,受压时为有利,取1.0;受拉时取1.2。
6.2.15
节点核芯区是保证框架承载力和延性的关键部位,为避免三级到二级承载力的突然变化,三级框架高度接近二级框架高度下限时,明显不规则或场地、地基条件不利时,可采用二级并进行节点核芯区受剪承载力的验算。
本次修订,增加了梁宽大于柱宽的框架和圆柱框架的节点核芯区验算方法。梁宽大于柱宽时,按柱宽范围内外分别计算。圆柱的计算公式依据国外资料和国内试验结果提出:
上式中Aj为圆柱截面面积,Ash为核芯区环形箍筋的单根截面面积。去掉γRE及ηi附加系数,上式可写为:
上式中最后一项系参考ACI Structural Journal Jan—Feb.1989 Priestley and Paulay 的文章:Seismic strength of Circular Reinforced Concrete Columns。
圆形截面柱受剪,环形箍筋所承受的剪力可用下式表达:
式中
:环形箍单肢截面面积;
:纵向钢筋所在圆周的直径;
:框架梁截面有效高度;
:环形箍筋间距。
根据重庆建筑大学2000年完成的4个圆柱梁柱节点试验,对比了计算和试验的节点核芯区受剪承载力,计算值与试验之比约为85%,说明此计算公式的可靠性有一定保证。