第附录C.1.1条
混凝土的多轴强度和本构关系可采用下列方法确定:
1. 制作试件并通过试验测定:
2. 选择合理形式的数学模型,由试验标定其中所需的参数值;
3. 采用经过试验验证或工程经验证明可行的数学模型。
第附录C.1.2条
本附录中所给出的各种数学模型适用于下述条件:混凝土强度等级;混凝土质量密度
;正常温度、湿度环境;正常加载速度。
第附录C.1.3条
本附录中,混凝土的应力-应变曲线和多轴强度均按相对值
、
、
、
、
和
等给出。其中,分母为混凝土的单轴强度(
或
)和相应的峰值应变(
或
)。
根据结构分析方法和极限状态验算的需要,单轴强度(或
)可分别取为标准值(
或
)、设计值(
或
)或平均值(
或
)。其中,平均值应按下列公式计算:
(C.1.3-1)
(C.1.3-2)
式中
、
: 混凝土抗压强度、抗拉强度的变异系数,宜根据试验统计确定。
第附录C.2.1条
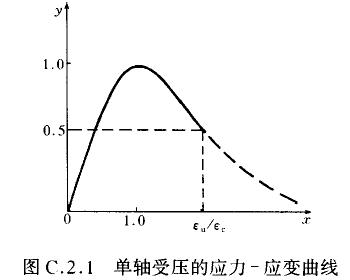
混凝土单轴受压的应力-应变曲线方程可按下列公式确定(图C.2.1):
当时
(C.2.1-1)
当时
(C.2.1-2)
(C.2.1-3)
(C.2.1-4)
式中
、
: 单轴受压应力-应变曲线上升段、下降段的参数值,按表C.2.1采用;
: 混凝土的单轴抗压强度(
、
或
);
: 与
相应的混凝土峰值压应变,按表C.2.1采用。
表C.2.1
|
混凝土单轴受压应力-应变曲线的参数值 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
f*c(N/mm2) |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
εc(×10-6) |
1370 |
1470 |
1560 |
1640 |
1720 |
1790 |
1850 |
1920 |
1980 |
2030 |
|
αa |
2.21 |
2.15 |
2.09 |
2.03 |
1.96 |
1.90 |
1.84 |
1.78 |
1.71 |
1.65 |
|
αd |
0.41 |
0.74 |
1.06 |
1.36 |
1.65 |
1.94 |
2.21 |
2.48 |
2.74 |
3.00 |
|
εu/εc |
4.2 |
3.0 |
2.6 |
2.3 |
2.1 |
2.0 |
1.9 |
1.9 |
1.8 |
1.8 |
※注:
为应力-应变曲线下降段上应力等于
时的混凝土压应变。
第附录C.2.2条
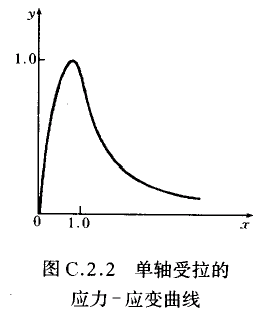
混凝土单轴受拉的应力-应变曲线方程可按下列公式确定(图C.2.2):
当时
(C.2.2-1)
当时
(C.2.2-2)
(C.2.2-3)
(C.2.2-4)
式中
: 单轴受拉应力-应变曲线下降段的参数值,按表C.2.2取用;
: 混凝土的单轴抗拉强度(
、
或
);
: 与
相应的混凝土峰值拉应变,按表C.2.2取用。
表 C.2.2
|
混凝土单轴受拉应力-应变曲线的参数值 |
|||||||
|---|---|---|---|---|---|---|---|
|
f*t(N/mm2) |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
|
εt(×10-6) |
65 |
81 |
95 |
107 |
118 |
128 |
137 |
|
αt |
0.31 |
0.70 |
1.25 |
1.95 |
2.81 |
3.82 |
5.00 |
第附录C.3.1条
二维、三维结构或处于多维应力状态的杆系结构的局部,由线弹性分析、非线性分析或试验方法求得应力分布和混凝土主应力值后,混凝土多轴强度验算应符合下列要求:
(C.3.1)
式中
: 混凝土主应力值:受拉为正,受压为负,且
;
: 混凝土多轴强度:受拉为正,受压为负,且
,宜按第C.3.2至C.3.4条的混凝土多轴强度相对值(
或
)计算。
第附录C.3.2条
在二轴(压-压、拉-压、拉-拉)应力状态下,混凝土的二轴强度可按图C.3.2所示的包络图确定。
第附录C.3.3条
在三轴受压(压-压-压)应力状态下,混凝土的抗压强度可根据应力比
按图C.3.3插值确定,其最高强度值不宜超过
。
第附录C.3.4条
在三轴拉-压(拉-拉-压、拉-压-压)应力状态下,混凝土的多轴强度可不计的影响,按二轴拉-压强度取值(图C.3.2)。
在三轴受拉(拉-拉-拉)应力状态下,混凝土的抗拉强度可取
。
第附录C.4.1条
混凝土在多轴应力状态下的破坏准则可采用下列一般方程表达:
(C.4.1-1)
(C.4.1-2)
(C.4.1-3)
(C.4.1-4)
(C.4.1-5)
式中
: 按混凝土多轴强度计算的八面体正应力;
: 按混凝土多轴强度计算的八面体剪应力;
、
、
、
、
: 参数值,宜由试验标定;无试验依据时可按下列数值取用:
。
第附录C.4.2条
混凝土的本构关系可采用非线弹性的正交异性模型,也可采用经过验证的其他本构模型。