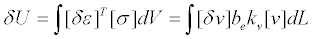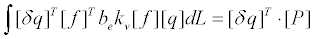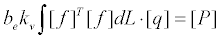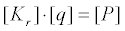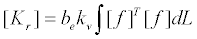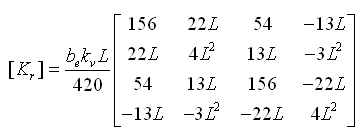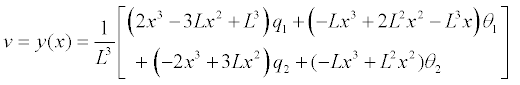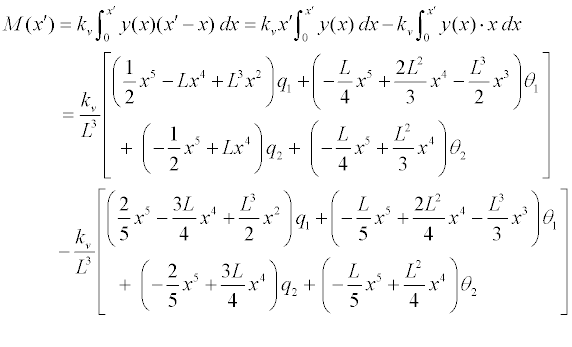|
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| 功能说明 | |||||||||||||||||||||||||||
|
1. 弹性地基法(弹性桩法) | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
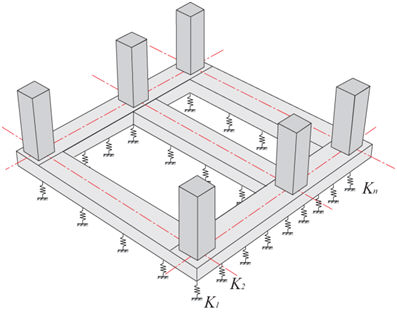
图17.3.1-1 弹性地基上的梁 | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
2. 梁单元计算公式
| |||||||||||||||||||||||||||
|
δu δε σ v δv k | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
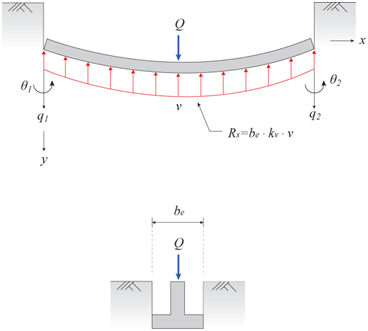
图17.1.3-2 弹性地基上的梁 | |||||||||||||||||||||||||||
|
内部虚应变能和外部虚功(external
virtual work)相同,所以可得如下公式:
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
式中, P f q kr 单元长度为L的弹性地基上的梁的文克儿弹簧(winkler spring)的刚度矩阵如下,该刚度与梁刚度叠加构成弹性地基上梁单元的最终刚度矩阵。
3. 文克尔(winkler)弹簧对梁单元内力的影响 梁单元的内部位移使文克尔(Winkler)弹簧产生内力,从而反过来也会影响梁的内力。梁单元任意位置x处的内部位移可使用节点位移 q 和 θ 按下式计算: | |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
文克尔(Winkler)弹簧引起的梁单元的剪力和弯矩可使用梁的位移和基床反力系数按下式计算,梁的内力加上文克儿弹簧的内力就是梁的最终内力值。
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
|
4. 倒楼盖法 | |||||||||||||||||||||||||||
|
|