| 技术原理 |
包含了非线性构件(分配了铰特性的构件)的运动方程如下:
|
|
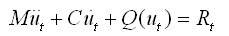 (4.2.1-1) (4.2.1-1) |
|
式中: |
|
M
——
质量矩阵;
C
——
阻尼矩阵;
Q(ut) —— 弹塑性恢复力;
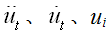 —— 在时间 时的各节点的加速度、速度、位移; —— 在时间 时的各节点的加速度、速度、位移;
Rt
——
节点上的动力荷载。 |
|
|
动力弹塑性分析属于非线性分析不能使用振型叠加法,程序提供Newmark-β直接积分方法。根据Newmark-β法的基本假定,使用t时刻的加速度、速度和位移表现t+Δt时刻的速度和加速度如下:
|
|
|
|
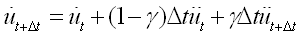 (4.2.1-2) (4.2.1-2) |
|
|
|
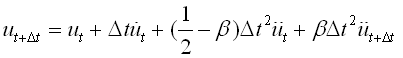 (4.2.1-3) (4.2.1-3) |
|
|
|
可重新整理上面公式如下: |
|
|
|
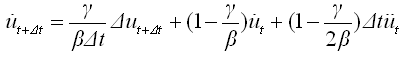 (4.2.1-4) (4.2.1-4) |
|
|
|
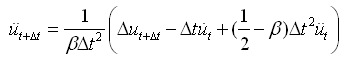 (4.2.1-5) (4.2.1-5) |
|
|
|
位移、速度、加速度增量为: |
|
|
|
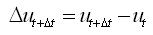 (4.2.1-6) (4.2.1-6) |
|
|
|
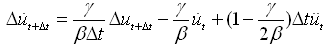 (4.2.1-7) (4.2.1-7) |
|
|
|
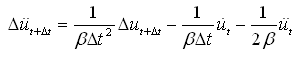 (4.2.1-8) (4.2.1-8) |
|
|
|
使用完全牛顿-拉普森计算的迭代增量为: |
|
|
|
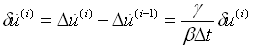 (4.2.1-9) (4.2.1-9) |
|
|
|
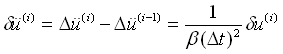 (4.2.1-10) (4.2.1-10) |
|
|
|
因此在时间t+Δt时的第(i)次迭代计算时的位移、速度、加速度为: |
|
|
|
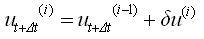 (4.2.1-11) (4.2.1-11) |
|
|
|
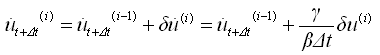 (4.2.1-12) (4.2.1-12) |
|
|
|
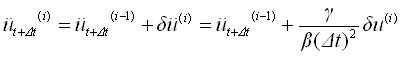 (4.2.1-13) (4.2.1-13) |
|
|
|
在时间t+Δt时的第(i)次迭代计算时的非线性运动方程如下: |
|
|
|
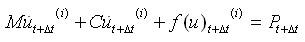 (4.2.1-14) (4.2.1-14) |
|
|
|
将(4.2.1-12)和(4.2.1-13)代入(4.2.1-14)可得对于位移增量δu(i)的平衡方程: |
|
|
|
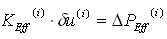 (4.2.1-15) (4.2.1-15) |
|
|
|
式中: |
|
KEff
——
有效刚度矩阵;
ΔPEff —— 各迭代计算中的有效荷载向量;
K(i)t+Δt
——
包含非线性单元的切线刚度矩阵;
δu(i)—— 各迭代计算中的位移增量向量;
β
——
Newmark-β法时间积分参数。 |
|
|
|
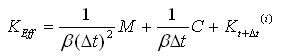 (4.2.1-16) (4.2.1-16) |
|
|
|
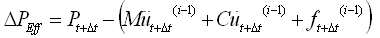 (4.2.1-17) (4.2.1-17) |
|
|
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
