| 技术原理 |
下面介绍梁柱单元的分析过程,其中省略了收敛迭代的计算过程,可参见静力弹塑性和动力弹塑性中的相关介绍。
|
|
(1)计算节点位移 |
|
利用非线性增量平衡方程计算节点位移增量ΔU,然后将其转换为单元坐标系增量Δu。 |
|
|
|
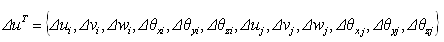 (5.2.2-1) (5.2.2-1) |
|
|
|
(2)将节点位移由总位移转换为相对位移 |
|
单元两端的总位移是包含了单元刚体移动的位移,而结构的内力是由扣除刚体位移的相对位移(变形)决定的。下面介绍轴向、扭转、旋转方向相对位移(变形)的计算过程。 |
|
① 单元的轴向变形:两端节点的轴向位移差为轴向变形。 |
|
|
|
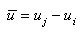 (5.2.2-2) (5.2.2-2) |
|
|
|
② 单元的扭转变形:两端节点的扭转角差为扭转变形。
|
|
|
|
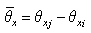 (5.2.2-3) (5.2.2-3) |
|
|
|
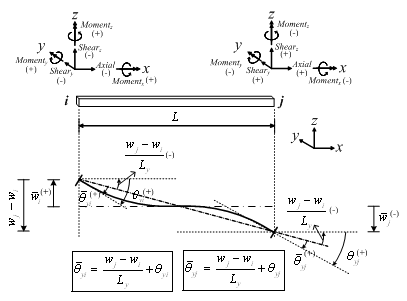
③ 单元的旋转角:如下图5.2.2-1所示由弯矩和剪力引起的变形角和刚体旋转角组成。
|
|
|
|
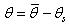 (5.2.2-4) (5.2.2-4) |
|
|
|
式中: |
|
θ
——节点位置总的旋转角; |
|
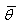 —— 弯矩和剪力引起的变形角; —— 弯矩和剪力引起的变形角; |
|
θs
——
刚体运动引起的旋转角。 |
|
|
|
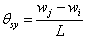 , ,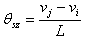 |
|
|
|
弯矩方向的内力-变形非线性关系中使用的是扣除刚体运动引起的旋转角的变形角,即 |
|
|
|
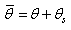 (5.2.2-5) (5.2.2-5) |
|
|
|
 |
|
|
|
图5.2.2-1 单元的绝对位移和相对位移的关系
|
|
|
|
将各方向的变形整理为单元的变形增量公式 如下: |
|
|
|
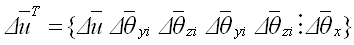 (5.2.2-6) (5.2.2-6) |
|
|
|
其中: |
|
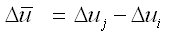 |
|
|
|
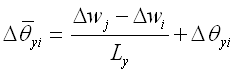 |
|
|
|
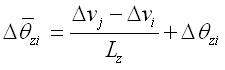 |
|
|
|
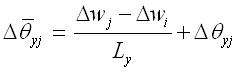 |
|
|
|
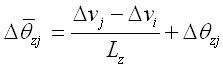 |
|
|
|
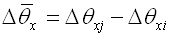 |
|
|
|
(3)利用单元的变形增量
计算单元的内力增量 |
|
单元的内力增量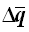 为单元的变形增量 为单元的变形增量 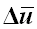 和使用扣除了刚体移动计算的切线刚度矩阵 和使用扣除了刚体移动计算的切线刚度矩阵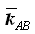 的乘积。单元的内力增量 的乘积。单元的内力增量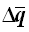 中的轴向力、扭矩、剪力为单元跨中值,弯矩则为单元两端值。 中的轴向力、扭矩、剪力为单元跨中值,弯矩则为单元两端值。
|
|
|
|
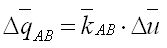 (5.2.2-7) (5.2.2-7) |
|
|
|
其中,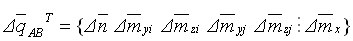 为单元的轴向力和弯矩的内力增量向量, 为单元的轴向力和弯矩的内力增量向量,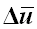 为单元的变形增量向量, 为单元的变形增量向量,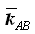 为扣除了刚体移动计算的单元的切线刚度矩阵。 为扣除了刚体移动计算的单元的切线刚度矩阵。 |
|
|
|
单元剪力的内力增量 可使用弯矩增量计算如下: |
|
|
|
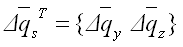 (5.2.2-8) (5.2.2-8) |
|
|
|
其中: |
|
|
|
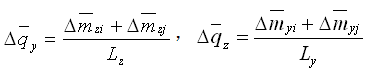 |
|
|
|
(4)使用单元的内力增量
和铰的柔度矩阵计算铰的变形增量 |
|
弯矩-旋转角型单元和弯矩-曲率型单元中,将单元的内力增量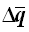 转换为非线性铰(截面)的内力增量Δq的方法是不同的,这将在各自单元的说明中另行阐述。得到铰(截面)的内力增量Δq后与铰的当前状态的柔度矩阵相乘可得铰(截面)的变形增量。 转换为非线性铰(截面)的内力增量Δq的方法是不同的,这将在各自单元的说明中另行阐述。得到铰(截面)的内力增量Δq后与铰的当前状态的柔度矩阵相乘可得铰(截面)的变形增量。
|
|
|
|
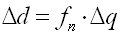 (5.2.2-9) (5.2.2-9) |
|
|
|
式中: |
|
fn
—— 弹塑性铰的柔度(fn=1/kn)。 |
|
|
|
(5)铰的总内力和总变形 |
|
铰的总内力和总变形为前次步骤的内力和变形与当前步骤的内力和变形的累加。 |
|
|
|
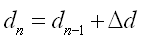 (5.2.2-10) (5.2.2-10) |
|
|
|
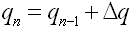 (5.2.2-11) (5.2.2-11) |
|
|
|
式中: |
|
dn-1
——
弹塑性铰的前次步骤的总的变形; |
|
qn-1
——
弹塑性铰的前次步骤的总的内力。 |
|
|
|
(6)铰的柔度和内力 |
|
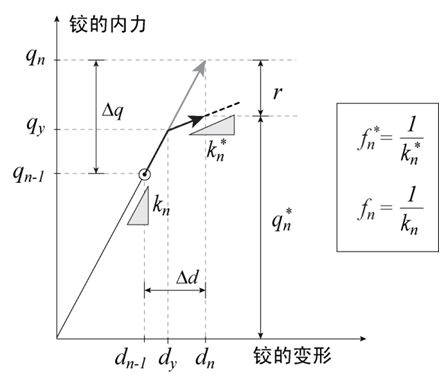
铰的柔度和内力的计算方法如图5.2.2-2所示,可采用的铰骨架曲线(或滞回曲线)按如下步骤计算: |
|
① 判断在前次步骤(n-1)向当前步骤(n)移动时,弹塑性铰的变形dn是否超过了屈服变形dy。当前步骤中的变形超过了屈服变形dy时,表示弹塑性铰的内力超过了屈服内力,表示铰发生了屈服。 |
|
② 当弹塑性铰的变形dn超过了屈服变形dy时,铰的刚度kn将使用骨架曲线中折减后的刚度kn*,并使用更新的刚度kn*计算柔度fn*。 |
|
③ 使用更新的刚度kn*计算铰的内力qn*。 |
|
④ 计算不平衡力r,且r=qn-qn* |
|
|
|
|
|
|
|
图5.2.2-2 弹塑性铰的内力和变形关系(骨架曲线) |
|
|
|
(7)计算单元的单元刚度矩阵和内力 |
|
使用通过骨架曲线计算的铰的柔度和内力计算单元的柔度矩阵和单元内力,单元的刚度矩阵为柔度矩阵的逆矩阵。 |
|
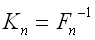 (5.2.2-12) (5.2.2-12) |
|
|
|
式中: |
|
Fn
——
非线性梁柱单元的柔度矩阵;
Kn
——
非线性梁柱单元的刚度矩阵。 |
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
