| 技术原理 |
对于面内和面外变形的计算公式参见结构大师《分析设计原理》技术手册中关于板单元的介绍,在此仅介绍位移-应变关系矩阵和刚度矩阵的计算方法。
|
|
(1)位移-应变的转换矩阵 |
|
竖向和水平向的应变由轴心受拉或受压应变与弯曲应变组成,单元内的任意位置的应变如下式所示: |
|
|
|
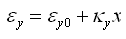 (5.3.2-1) (5.3.2-1) |
|
|
|
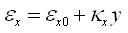 (5.3.2-2) (5.3.2-2) |
|
|
|
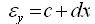 (5.3.2-3) (5.3.2-3) |
|
|
|
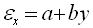 (5.3.2-4) (5.3.2-4) |
|
式中: |
|
εy、εx
——
单元内任意点的竖向和水平向应变;
εy0、εx0
——
中和轴位置的竖向/水平向应变;
κy、κx
——
竖向/水平向的曲率。 |
|
|
|
使用最小二乘法计算单元内任意位置的位移-应变关系矩阵如下: |
|
|
|
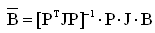 (5.3.2-5) (5.3.2-5) |
|
|
|
式中: |
|
P
——
单元内任意位置的坐标矩阵;
B
——
积分点位置的位移-应变关系矩阵;
J
——
积分点位置的雅可比矩阵;
B——
单元内任意位置的位移-应变关系矩阵。 |
|
|
|
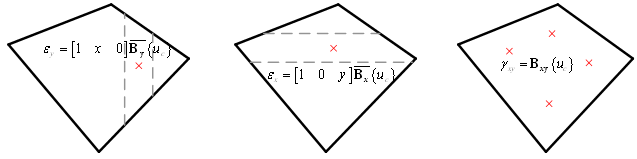
对于剪切成分使用高斯积分点位置的变形-应变关系矩阵,如图5.3.2所示分别为竖向、水平向、剪切方向的应变。图中
为使用最小二乘法计算的竖向和水平向位移-应变关系矩阵,Bxy是剪切变形-剪切应变的关系矩阵,{uc}是单元的位移向量。 |
|
|
|
|
|
|
|
(a) 竖向应变 (b)
水平应变 (c)
剪切应变 |
|
|
|
图5.3.2 各应变成分 |
|
|
|
(2)单元刚度矩阵 |
|
因为前面已经假设单元的竖向、水平、剪切方向的变形成分互相独立,因此各方向的刚度也是相互独立的。 |
|
① 竖向刚度 |
|
|
|
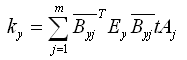 (5.3.2-6) (5.3.2-6) |
|
|
|
式中: |
|
m
——
竖向纤维数量;
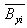 —— 竖向第j个纤维的位移-应变关系矩阵; —— 竖向第j个纤维的位移-应变关系矩阵;
Ey
——
Ey=Ecy+ρyEsy;
Ecy
——
竖向混凝土的弹性模量;
Esy
——
竖向钢筋的弹性模量;
ρy
——
竖向钢筋配筋率;
Aj
——
竖向第j个纤维的面积;
t
——
单元厚度。 |
|
|
|
② 水平方向刚度 |
|
|
|
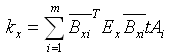 (5.3.2-7) (5.3.2-7) |
|
式中: |
|
n
——
水平方向的纤维数量;
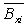 —— 水平方向第i个纤维的位移-应变关系矩阵; —— 水平方向第i个纤维的位移-应变关系矩阵;
Ex
——
Ex=Ecx+ρxEsx;
Ecx——水平方向混凝土弹性模量;
Esx
——
水平方向钢筋的弹性模量;
ρx——
水平方向钢筋配筋率;
Ai
——
水平方向第i个纤维的面积;
t
——
单元厚度。 |
|
|
|
③ 剪切刚度 |
|
|
|
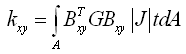 (5.3.2-8) (5.3.2-8) |
|
式中: |
|
G
——
剪切模量。 |
|
|
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
