| 技术原理 |
下面介绍混凝土、钢筋、墙单元剪切特性本构关系的使用方法。
|
|
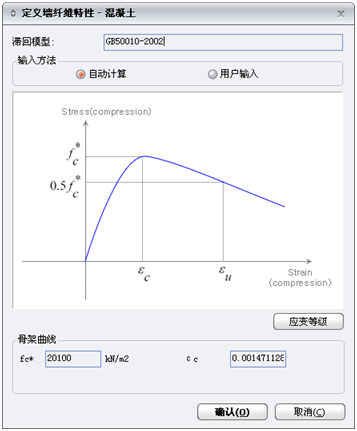
(1)混凝土材料的本构关系采用了混凝土结构设计规范(GB 50010-2002)附录C.2.1中提供的单轴受压曲线,在首选项中的混凝土参数值只是示意值,分配到具体构件时,程序会根据各构件的材料强度等级自动计算各构件的材料非线性参数。用户可在非线性工作目录树中查看具体构件的非线性参数。 |
|
|
|
|
|
图8.4-1
混凝土材料的本构关系 |
|
|
|
混凝土单轴受压的应力-应变曲线方程可按下列公式确定(图8.4-1): |
|
当x≤1时 |
|
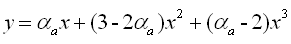 (8.4-1) (8.4-1) |
|
|
|
当x>1时 |
|
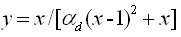 (8.4-2)
(8.4-2) |
|
|
|
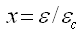 (8.4-3)
(8.4-3) |
|
|
|
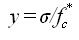 (8.4-4)
(8.4-4) |
|
|
|
另外,条文说明中公式为: |
|
|
|
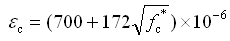
|
|
|
|
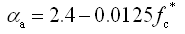
|
|
|
|
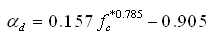 |
|
|
|
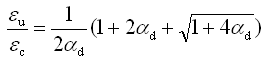
|
|
|
|
式中: |
|
αa、 αd
——
单轴受压应力-应变曲线上升段、下降段的参数值;
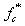 —— 混凝土的单轴抗压强度,程序在非线性分析中使用了混凝土的抗压强度标准值fck; —— 混凝土的单轴抗压强度,程序在非线性分析中使用了混凝土的抗压强度标准值fck;
εc
——
与 相应的混凝土峰值压应变;
εu
——
为应力-应变曲线下降段上应力等于0.5 时的混凝土压应变。 |
|
|
|
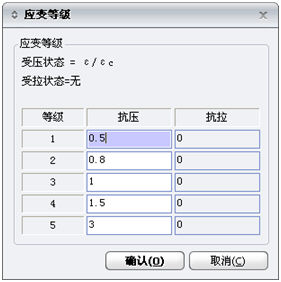
混凝土材料本构关系对话框中的" 应变等级" 键用于定义混凝土材料所处的受力状态应变级别。第1等级可认为是弹性状态,第2等级可认为是开裂状态,第3等级可定义为屈服状态,第4等级可认为是屈服后状态,第5等级可认为是极限状态。极限状态的极限压应变值与混凝土材料强度相关,一般在1.8~4.2之间,常用材料强度约为2.0,可按前面公式计算。
|
|
|
|
 |
|
|
|
图8.4-2
混凝土材料应变等级 |
|
|
|
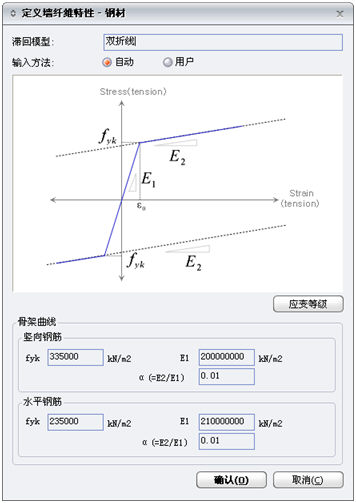
(2)钢筋的材料本构关系使用双折线,程序认为钢筋是理想弹塑性材料,但为了计算的收敛性第二段直线的斜率采用了0.01。在首选项中的参数值只是示意值,分配到具体构件时,程序会根据各构件的材料强度等级自动计算各构件的材料非线性参数。用户可在非线性工作目录树中查看具体构件的非线性参数。
|
|
|
|
|
|
图8.4-3 钢筋材料的本构关系 |
|
钢筋材料本构关系对话框中的"应变等级"
键用于定义钢筋所处的受力状态级别。第1等级可认为是弹性状态,第2等级可认为是屈服状态,第3和第4等级可定义为屈服后状态,第5等级可认为是极限状态。 |
|
|
|
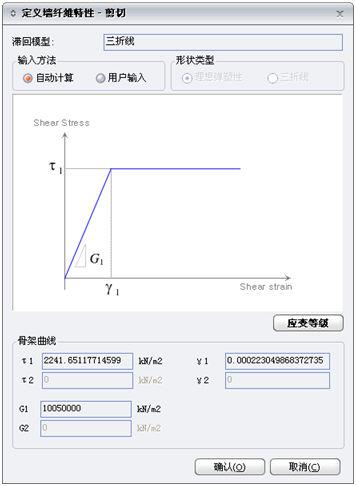
(3)墙单元的剪切特性材料本构关系使用三折线,但程序内部默认使用理想弹塑性材料,即将第二和第三折线段的斜率设为零。对于剪切特性,程序仅对理想弹塑性本构模型提供自动计算特性功能。在形状类型中可选择理想弹塑性(E-P-P类型,即双折线类型)和剪力退化类型(三折线类型)。 |
|
 |
|
图8.4-5
墙单元剪切特性 |
|
|
|
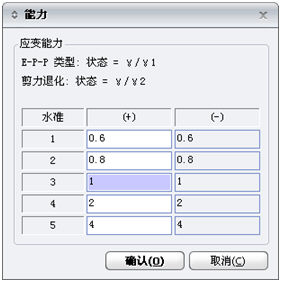
墙单元剪切特性本构关系对话框中的"应变等级"键用于定义墙单元所处的受力状态级别。对于理想弹塑性(双折线类型),第1和第2等级可认为是弹性状态,第3等级可认为是屈服状态,第4等级可定义为屈服后状态,第5等级可认为是极限状态。对于剪力退化模型(三折线类型),状态根据输入的数据决定。 |
|
|
|
|
|
|
|
图8.4-6
墙单元剪切应变等级 |
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
