| 技术原理 |
能力谱和需求谱的交点为性能点,结构大师中使用ATC-40的能力谱法(CSM)中推荐的Procedure-A和Procedure-B两种方法计算性能点。两种方法的原理相同,Procedure-A在计算有效阻尼时使用直接迭代计算,而Procedure-B则是使用延性比的假定和有效周期计算有效阻尼。
|
|
(1)等效阻尼(equivalent
damping) |
|
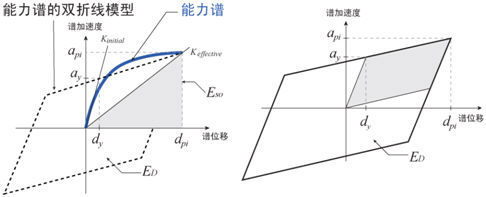
能力谱法(CSM)中将能力谱转换为面积相同的双折线模型,并使用阻尼比为5%的弹性响应谱和能力谱计算结构的等效阻尼。结构阻尼耗散的能量等于双折线模型中的阴影面积,可使用下式(3.3.2-1)计算。
|
|
|
|
|
|
|
|
图3.3.2-1
使用骨架曲线计算等效阻尼 |
|
|
|
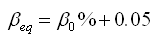 (3.3.2-1) (3.3.2-1) |
|
|
|
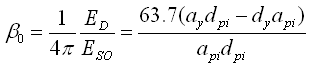
|
|
|
|
式中: |
|
ED
——
结构阻尼耗散的能量;
ESO
——
结构的最大变形能。 |
|
|
|
将式(3.3.2-1)用百分比的形式表现如下: |
|
|
|
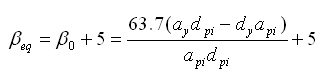 (3.3.2-2) (3.3.2-2) |
|
|
|
其中βeq为等效阻尼(%),当其超过25%时ATC-40要求慎重使用,且不能超过50%。
|
|
|
|
(2)有效阻尼(effective
damping) |
|
钢筋混凝土的滞回曲线不能准确反映钢筋混凝土的刚度退化(stiffness
degradation)和强度损伤(strength
deterioration)、滑移和挤压(slip
or pinching)等特性,为了能反映这些特性,ATC-40使用了阻尼修正系数(damping
modification factor)对等效阻尼进行调整,调整后的等效阻尼被称为有效阻尼。 |
|
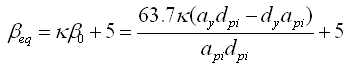 (3.3.2-3) (3.3.2-3) |
|
|
|
阻尼修正系数如下: |
|
反映结构滞回特性的阻尼修正系数
表3.3.2-1 |
|
结构响应类型 |
等效阻尼β0 (%) |
阻尼修正系数(κ) |
|
类型 A
(具有完整的滞回特性) |
≤16.25 |
1.0 |
|
> 16.25 |
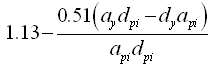
|
|
类型 B
(一般的滞回特性) |
≤25 |
0.67 |
|
> 25 |
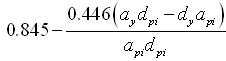
|
|
类型
C
(较差的滞回特性) |
所有值 |
0.33 |
|
|
(3)有效周期 |
|
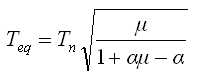 (3.3.2-4)
(3.3.2-4) |
|
|
|
式中: |
|
Tn
——
结构周期,可取地震作用方向的第一振型;
μ
——
延性比;
α
——
α
= (αpi-αy) / (dpi-dy)
。 |
|
|
|
(4)非弹性需求谱 |
|
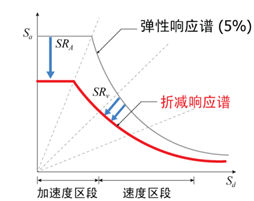
下面介绍使用有效阻尼计算非弹性需求谱的方法。使用有效阻尼系数分别计算加速度影响区段和速度影响区段的谱折减系数(spectrum
reduction factor, SR)(见图
3.3.2-2)。谱折减系数可使用Newmark和Hall(1982)推荐的地面运动放大系数计算,加速度区段的谱折减系数(SRA)和速度区段的谱折减系数(SRV)的计算式见(3.3.2-5)。
ATC-40中对不同结构响应类型规定了谱折减系数的下限值。 |
|
|
|
|
|
图3.3.2-2
使用谱折减系数对弹性谱进行折减 |
|
|
|
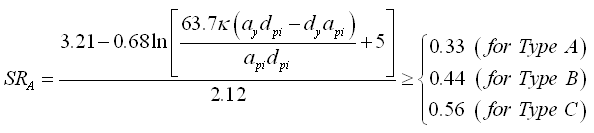
|
|
|
|
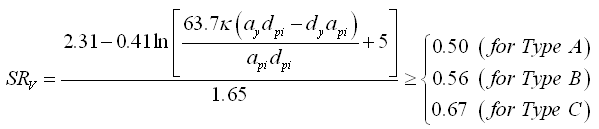 (3.3.2-5) (3.3.2-5) |
|
|
|
结构响应类型对应的谱折减系数的下限值
表3.3.2-2 |
|
结构响应类型 |
κ |
SRA
|
SRV |
|
Type
A
(完整滞回特性) |
1.00
|
0.33
|
0.50 |
|
Type
B
(一般滞回特性) |
0.67 |
0.44
|
0.56 |
|
Type
C
(较差滞回特性) |
0.33 |
0.56
|
0.67 |
|
|
通过对弹性反应谱的折减可得弹塑性需求谱,该弹塑性需求谱是阻尼比为5%的弹塑性需求谱,计算性能点还需要通过计算有效阻尼对应的需求谱。下面介绍计算性能点的方法。
|
|
|
|
(5)计算性能点的方法 |
|
结构大师中按照ATC-40的推荐的两种方法计算性能点,两种方法都是通过计算有效阻尼获得需求谱,并计算需求谱与能力谱的交点的方法。 |
|
①
Procedure-A方法 |
|
|
|
|
|
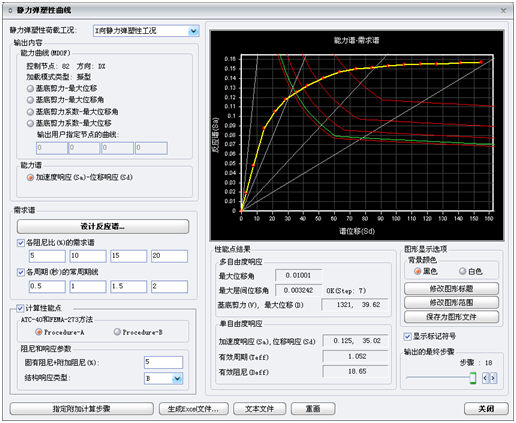
图3.3.2-3
使用Procedure-A方法计算性能点(结构大师) |
|
|
|
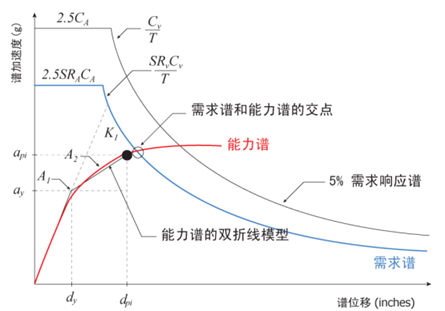
是ATC-40中提供的基本方法,其步骤如下(见图3.3.2-4):
a. 首先获得能力谱的初始切线刚度直线与阻尼比为5%的弹性需求谱的交点,将该交点作为初始性能点。
b. 计算初始性能点上的等效阻尼以及有效阻尼,利用有效阻尼计算弹塑性需求谱,并获得弹塑性需求谱与能力谱的交点,即获得新的性能点。
c. 反复计算上述过程当性能点上的响应位移和响应加速度满足程序内部设置的误差范围时,将该步骤的性能点作为最终性能点。 |
|
|
|
|
|
图3.3.2-4
使用Procedure-A方法计算性能点的示意图(ATC-40) |
|
|
|
② Procedure-B方法 |
|
|
|
|
|
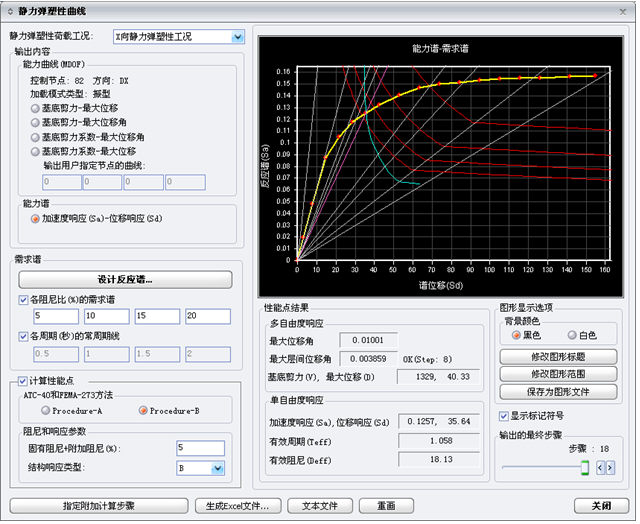
图3.3.2-5
使用Procedure-B方法计算性能点(结构大师) |
|
|
|
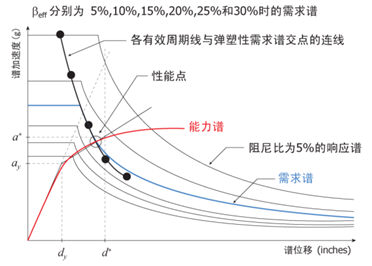
计算性能点的操作步骤如下(见图3.3.2-6):
a.
首先假设一个位移延性系数,使用位移延性系数计算结构的有效周期和有效阻尼,然后获得有效周期线(直线)与弹塑性需求谱(使用有效阻尼计算)的交点。
b.
这样一系列的交点上的连线与能力谱的交点就是最终的性能点。 |
|
|
|
|
|
图3.3.2-6
使用Procedure-B方法计算性能点的示意图(ATC-40) |
|
|
|
Procedure-B方法具有收敛性能好的优点,并且只需要计算一系列不同有效阻尼比和有效周期对应的加速度谱值和位移谱值的点即可,因此计算方法也相对简单。 |
|
|
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
