| 技术原理 |
|
(1)弯矩-旋转角梁柱单元的各成分的非线性特性 |
|
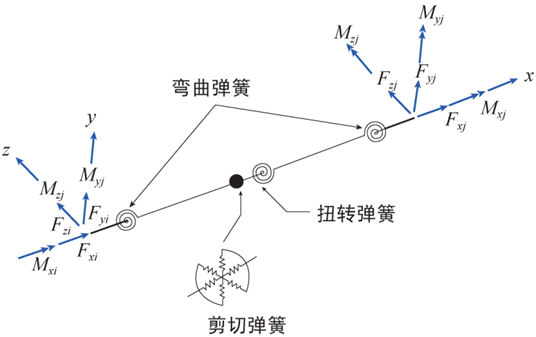
弯矩-旋转角梁柱单元是在单元两端设置了长度为0的平动和旋转非线性弹簧,而单元内部为弹性的非线性单元类型,如下图5.2.3-1所示非线性弹簧的位置示意图。
|
|
|
|
|
|
|
|
图5.2.3-1
弯矩-旋转角单元的铰位置示意图 |
|
|
|
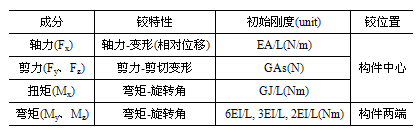
弯矩-旋转角单元各成分非线性特性
表5.2.3
|
|
|
|
|
|
(2)弯矩-旋转角梁柱单元的柔度矩阵 |
|
弯矩旋转角单元的柔度矩阵由弹塑性铰的柔度矩阵和弹性梁柱单元的柔度矩阵相加而成,弹塑性铰的柔度为用户定义的铰的切线柔度和初始柔度的差,单元屈服前为零,铰的切线柔度矩阵由单轴(Single Component)或多轴(P-M-M)模型的状态决定。 |
|
|
|
弯矩-旋转角梁柱单元的分析过程如下:
|
|
①通过在前面第5.2.2节中介绍的(1)~(6)的计算过程获得铰的柔度和内力。因为在弯矩-旋转角梁柱单元中,计算的内力增量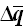 的位置就是铰的位置,所以铰的内力Δq直接使用单元的内力增量 的位置就是铰的位置,所以铰的内力Δq直接使用单元的内力增量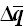 。 。 |
|
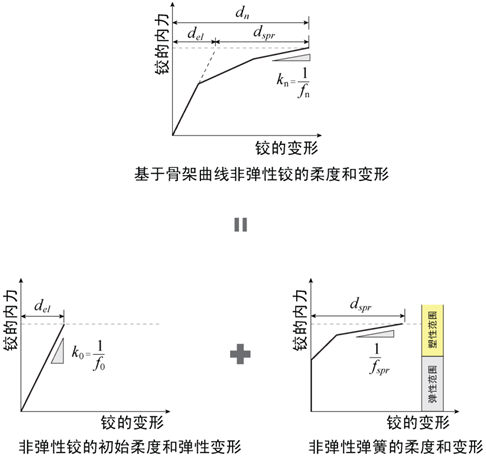
②使用图5.2.3-2(a)的骨架曲线计算的各成分的铰的柔度,分为初始状态的柔度和弹塑性铰的柔度两个部分。
|
|
|
|
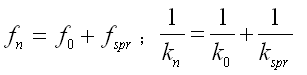 (5.2.3-1) (5.2.3-1) |
|
|
|
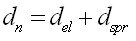 (5.2.3-2) (5.2.3-2) |
|
|
|
式中: |
|
fn
——
由骨架曲线计算的铰的柔度; |
|
fn
——
初始柔度; |
|
fspr
——
非线性弹簧的柔度; |
|
dn
——
弹塑性铰的变形; |
|
del
——
弹性变形; |
|
dspr
——
非线性弹簧的塑性变形。 |
|
|
|
|
|
|
|
图5.2.3-2
弹塑性铰的柔度 |
|
|
|
非线性弹簧的柔度如下: |
|
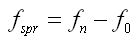 (5.2.3-3) (5.2.3-3) |
|
|
|
弹塑性梁柱单元的柔度矩阵可由弹性梁单元的柔度矩阵和非线性弹簧的柔度矩阵相加而得:
|
|
|
|
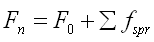 (5.2.3-4) (5.2.3-4) |
|
|
|
式中: |
|
Fn
——
弹塑性梁柱单元的柔度矩阵; |
|
F0
——
弹性梁单元的柔度矩阵; |
|
Σfspr
——
非线性弹簧的柔度矩阵(弹性状态时为0)。 |
|
|
|
只有铰内力达到屈服内力时,才会产生非线性弹簧铰,所以在弹性范围内非线性铰的的柔度为0,即屈服前梁柱单元的柔度矩阵与弹性梁柱单元的柔度矩阵相同,所以用户输入的铰的初始刚度在单元屈服前对分析结果没有影响。
弯矩-旋转角梁柱单元的刚度矩阵可由弹塑性梁柱单元的柔度矩阵取逆计算。 |
|
|
|
(3)弯矩-旋转角梁柱单元弯矩成分的弹塑性铰的初始刚度 |
|
弯矩铰的弯矩-旋转角的关系不仅受单元端部的弯矩的影响,而且受单元内弯矩分布的影响,所以在定义铰的弯矩-旋转角关系时,需要定义弯矩在单元内的分布规律。一般来说按照图5.2.3-3~图5.2.3-
5所示通过定义端部具有弯矩作用的简支梁的初始刚度矩阵来模拟单元内弯矩分布的影响。 |
|
|
|
① 两端弯矩值相同方向相反时 |
|
|
|
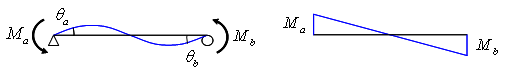
|
|
|
|
(a) 变形形状 (b)
弯矩分布 |
|
|
|
图5.2.3-3
两端弯矩大小相同方向相反的简支梁 |
|
|
|
二维梁单元的弯矩-位移关系如下: |
|
|
|
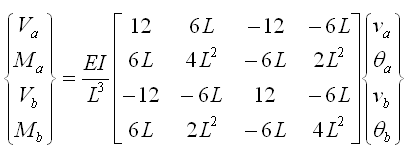 (5.2.3-5) (5.2.3-5) |
|
|
|
图5.2.3-3的va=vb=0、θa=θb,所以可将上式写为:
|
|
|
|
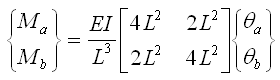 (5.2.3-6) (5.2.3-6) |
|
|
|
所以有: |
|
|
|
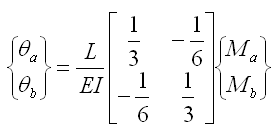 (5.2.3-7) (5.2.3-7) |
|
|
|
因为有θa=θb、Ma=Mb,所以有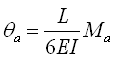 、 、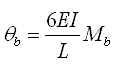 。 。 |
|
|
|
因此两端承受大小相同方向相反弯矩的梁单元的初始柔度和初始刚度如下:
|
|
|
|
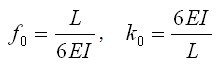 (5.2.3-8) (5.2.3-8) |
|
|
|
② 仅一端有弯矩作用时 |
|
|
|
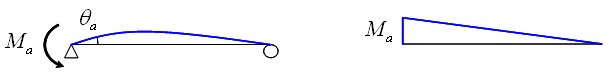 |
|
|
|
(a) 变形形状 (b)
弯矩分布 |
|
|
|
图5.2.3-4
仅一侧有弯矩作用的简支梁(Mb=0) |
|
|
|
图5.2.3-4的va=vb=0、Mb=0,所以可将式(5.2.3-5)写成如下: |
|
|
|
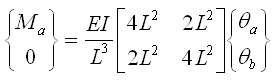 (5.2.3-9) (5.2.3-9) |
|
|
|
所以有: |
|
|
|
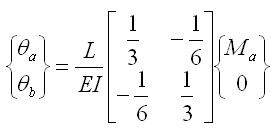 (5.2.3-10) (5.2.3-10) |
|
|
|
所以有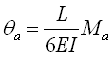 ,即仅有一侧有弯矩的梁单元的初始柔度和初始刚度如下: ,即仅有一侧有弯矩的梁单元的初始柔度和初始刚度如下: |
|
|
|
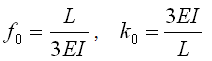 (5.2.3-11) (5.2.3-11) |
|
|
|
③ 两端弯矩大小相同且符号相同时(Mb=-Ma) |
|
|
|
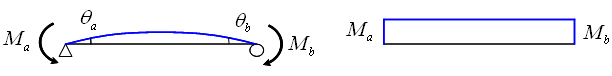
|
|
|
|
(a) 变形形状 (b)
弯矩分布 |
|
|
|
图5.2.3-5
两端弯矩大小相同方向相同的简支梁 |
|
|
|
图5.2.3-5的va=vb=0、Mb=-Ma,所以可将式(5.2.3-5)写成如下: |
|
|
|
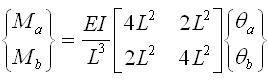 (5.2.3-12) (5.2.3-12)
|
|
|
|
所以有: |
|
|
|
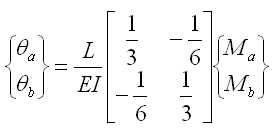 (5.2.3-13) (5.2.3-13) |
|
|
|
所以两端弯矩大小相同且符号相同的梁单元的初始柔度和初始刚度如下: |
|
|
|
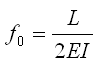 , ,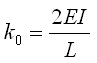 (5.2.3-14) (5.2.3-14) |
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
