| 技术原理 |
|
(1)弯矩-曲率梁柱单元的各成分的非线性特性 |
|
|
|
|
|
|
|
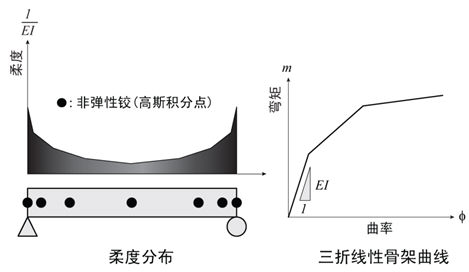
图5.2.4-1
弯矩-曲率型梁柱铰 |
|
|
|
弯矩-曲率型梁柱单元的特点如下:
①
弹塑性铰:指定积分点(可设置1~20个)。
②
可沿单元全长考虑弹塑性。
③ 对不同成分可指定不同的积分点(铰位置)。 |
|
弯矩-曲率单元各成分的非线性特性
表5.2.4 |
|
成 分 |
弹塑性铰特性 |
初始刚度(unit) |
铰位置 |
|
轴力(Fx)
|
轴力-应变 |
EA(N) |
积分点位置 |
|
剪力(Fy、Fz)
|
剪力-剪切应变 |
GAs(N)
|
积分点位置 |
|
扭矩(Mx) |
弯矩-曲率 |
GJ(Nm2) |
积分点位置 |
|
弯矩(My、Mz)
|
弯矩-曲率 |
EI(Nm2) |
积分点位置 |
|
|
|
|
(2)弯矩-曲率型梁柱单元的柔度矩阵 |
|
弯矩-曲率型梁柱单元的柔度矩阵是通过对各积分点的柔度进行积分计算获得的,弹塑性铰的切线柔度矩阵由单轴或多轴铰模型的状态决定。
弯矩-曲率型弹塑性梁柱单元的分析过程如下: |
|
① 通过在前面第5.2.2节中介绍的(1)~(3)的计算过程获得单元的内力增量 ,各积分点位置的弹塑性铰的内力增量Δq(x)可使用单元内力增量
的内插 函数(force
interpolation function)按下式计算。 |
|
a. 轴力和弯曲成分的铰内力增量 |
|
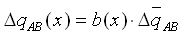 (5.2.4-1) (5.2.4-1) |
|
|
|
其中: |
|

|
|
|
|
b.
剪切成分的铰的内力增量 |
|
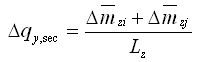
|
|
|
|
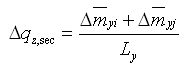
|
|
|
|
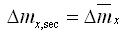 (5.2.4-2) (5.2.4-2) |
|
|
|
式中: |
|

|
|
|
|
② 通过在第5.2.2节中的(4)~(6)的计算过程计算各积分点的柔度f(x)和内力。
③
将各积分点的各成分的柔度f(x)通过数值积分得到梁柱单元的柔度矩阵: |
|
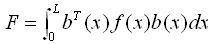 (5.2.4-3) (5.2.4-3) |
|
式中: |
|
f(x) —— 在位置x的截面的柔度矩阵;
b(x) —— 在位置x的内力分布函数(内插函数);
F
——
单元柔度矩阵;
L
——
单元长度;
x
——
截面(积分点)的位置。 |
|
|
|
④ 弯矩-曲率型弹塑性梁柱单元的刚度矩阵可对柔度矩阵取逆矩阵而得。 |
|
|
|
|
|
|
|
(4)弯矩-曲率型弹塑性梁柱单元的数值分析 |
|
梁柱单元的弹塑性特性主要发生在构件端部,而高斯-勒让德(Gauss-Legendre)积分法无法将构件端部作为积分点,所以结构大师中使用了高斯-罗贝托(Gauss-Lobatto)积分法计算单元的柔度矩阵。
积分点的数量意味着单元内的弹塑性铰的数量,可指定的数量为1~20个。如图5.2.4-2所示,积分点的位置与积分点的数量相关,离端部越近积分点的间距越小。因为高斯-罗贝托积分法无法处理两个积分点的情况,所以当积分点为两个时,程序内部使用了古典高斯积分法(Classical
Gauss Integration)构建了柔度矩阵。
分析结果的准确性与积分点的数量没有必然的联系,而积分点数量的增多会增加分析时间。经大量的分析比较当积分点的数量等于5个及以上时,分析结果的差异不大,所以一般可取5个积分点。 |
|
|
|
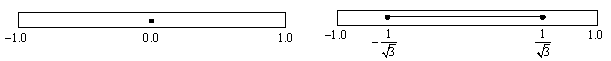
(a) 积分点=1 (b)
积分点=2
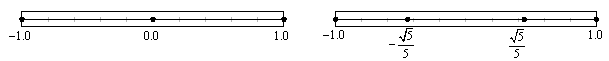
(c) 积分点=3 (d)
积分点=4
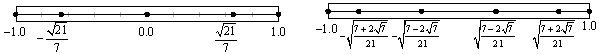
(e) 积分点=5 (f)
积分点=6 |
|
|
|
图5.2.4-2
高斯-罗贝托积分法的积分点位置 |
|
|
 |
|
1 |

|
动力弹塑性分析的一键式操作方法 |
|
