图7.2.8-1  武田三折线模型

（2）定义骨架曲线

非线性特性用下面参数定义：

P1(+)、P1(-) —— 正向和负向的第一屈服强度；

 P2(+)、P2(-) —— 正向和负向的第二屈服强度；

D1(+)、D1(-) —— 正向和负向的第一屈服变形；

 D2(+)、D2(-)—— 正向和负向的第二屈服变形；

                  K0 —— 初始刚度；

K2(+)、K2(-)  —— 正向和负向的第二条折线的刚度，K2(+)=α1(+)∙K0，K2(-)=α1(-)∙K0；

  K3(+)、K3(-)—— 正向和负向的第三条折线的刚度，K3(+)=α2(+)∙K0，K3(-)=α2(-)∙K0；

   α1(+)、α1(-)—— 正向和负向第一屈服后刚度折减系数；

  α2(+)、α2(-) —— 正向和负向第二屈服后刚度折减系数。

                     β —— 计算卸载刚度的幂阶；

                     α —— 内环卸载刚度折减系数，用于对内环的卸载刚度进行折减，。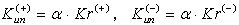

（3）武田三折线滞回模型的路径移动规则

①  时，为线弹性状态，沿着经过原点斜率为K0的直线移动(Rule:0)。

② 变形D初次超过D1(±)时，沿着第二条折线的斜率K2(+)、K2(-) 移动(Rule:1)；

在第二条折线移动时卸载，将沿着指向反向最大变形点移动，反向没有发生屈服时，反向第一屈服点为最大变形点(Rule:2)；在到达反向变形最大点之前重新加载时，将沿着相同的卸载直线移动(Rule:3)；当达到骨架曲线位置时，重新沿着斜率为K2(+)、K2(-)的骨架曲线移动(Rule:4)。

图7.2.8-2  变形D初次超过D1(±)时的路径移动规则

③ 变形D初次超过D2(±)时，沿着第三条折线的斜率K3(+)、K3(-)移动(Rule:13)；此时卸载时，将沿着斜率为Kr(+)、Kr(-)的直线移动(Rule:15)；反向为发生第一屈服前时斜率kr(±)的范围为P1，超过P1时将向第二屈服点移动(Rule:17)。

               其中，

 β：计算卸载刚度的幂阶( β=0.4，Default)

图7.2.8-3  变形D初次超过D2(±)时的路径移动规则

④ 超过恢复力为0的点时将向反向最大变形点移动(Rule:18)；

在向反向最大变形点移动时卸载，则开始进入内环(Rule:20)；

在内环中到恢复力为0的点之前按照斜率为Kun(-)、Kun(+)的直线卸载，超过恢复力为0的点后将向反向的之前卸载点移动(Rule:21)

图7.2.8-4  超过恢复力为0的点时的路径移动规则