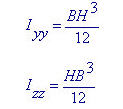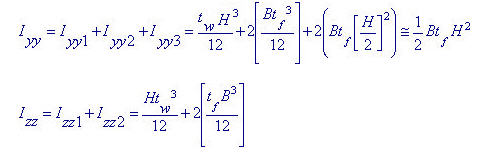Section
|
|
|
|
|
|
Enter section properties for line elements (Truss, Tension-only, Compression-only, Cable, Gap, Hook, Beam Element). |
|
|
|
|
|
|
|
From the Main Menu select Model > Properties > Section.
Select Geometry > Properties > Section in the Menu tab of the Tree Menu.
Click |
|
|
|
|
|
Properties (Section) dialog box
Click
Select the section to be modified from the
list in the Section dialog box and click
Select the section to be deleted from the
list in the Section dialog box and click
Select the section to be copied from the
list in the Section dialog box and click
Click Section List Selected
List Note Numbering
Type Keep
ID New
ID
Select the section property numbers to be
renumbered from the list in the Properties dialog box and modify the related
data followed by clicking
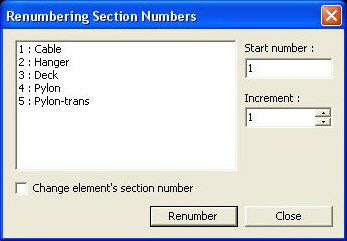
Renumbering Section Number dialog box
Start
number Increment Change
element's material number
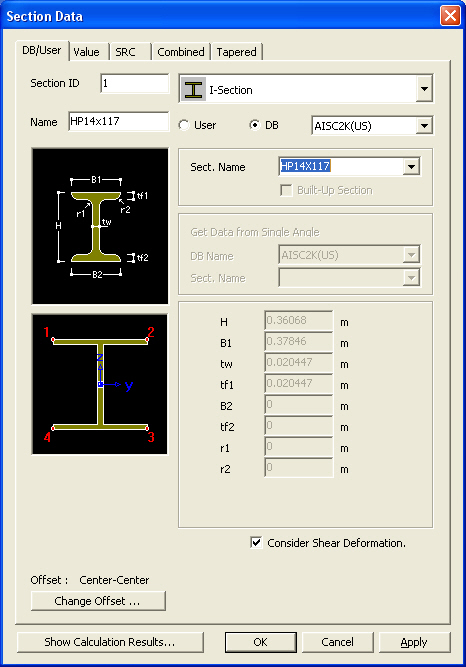
Section Data Dialog
Section ID
Section number (Auto-set to the last section number +1)
Note Up to 999999 Section ID's can be assigned.
Name
Section name (Sect. Name by default if not specified)
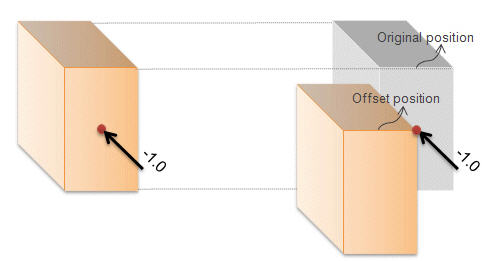
OffsetDisplay the section Offset currently set.
Location of the Centroid of a section is set as default. Click
Change Offset dialog box
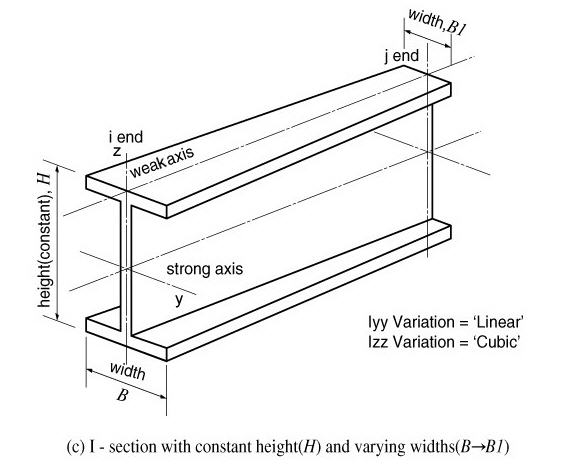
Offset: Specify the section Offset from the location options shown in the figure below.
Horizontal Offset: Specify the Offset in the transverse direction. "to Extreme Fiber" assigns the offset to the outer-most point. For a specific location of Offset, select 'User"and enter the distance from the "Centroid" to the desired Offset location. Unless the Offset is "Center-Center" the Horizontal Offset can be entered as the "User" type. For a tapered (non-prismatic) section, data input for the J-end also becomes activated.
Vertical Offset: Specify the Offset in the vertical direction. "to Extreme Fiber" assigns the offset to the outer-most point. For a specific location of Offset, select "User" and enter the distance from "Centroid" to the desired Offset location. Unless the Offset is "Center-Center" the Vertical Offset can be entered as the "User" type. For a tapered (non-prismatic) section, data input for the J-end also becomes activated.
Note 1 When Offset distance is specified, a positive (+) sign applies to Center-to-outward for Centroid reference and Extreme-to-inward for Extreme Fiber reference.
User Offset Reference: When section offset distance is specified as the "User" type, define the reference location.
Centroid: Specify the offset distance relative to the centroid of the section.
Extreme Fiber(s): Specify the offset distance relative to Left/Right & Top/Bottom.
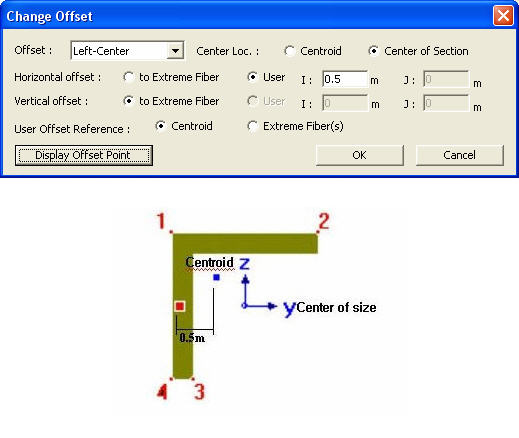
Note 2 When User type is specified, the Offset distance and direction are entered relative to Centroid irrespective of the Center option (Centroid or Center of Section). For example, specifying "Offset: Left-Center", "Center Loc.: Center of Section" and "Horizontal offset: 0.5 " User type" will result in an Offset 0.5" to the left of the Centroid. And if the Offset option is "Left-Center" and the Center option is Center of Section the User type for Horizontal offset becomes activated and the User type for Vertical offset becomes inactivated. The Horizontal offset defined as User type here becomes the Centroid, and the Vertical offset fixed to Center becomes the "Center of Section"
Note 3 When FCM Wizard is used, and "Apply the Centroid of Pier Table Section Option" is selected, the node locations of the girder will be changed as follows: Offset: Center-Top User Offset Reference: Extreme Fiber(s) Vertical Offset: User, Offset Distance (i & j) = Pier Table section height-Centroid of Pier Table section
Note 4 Usage tip of Section Offset
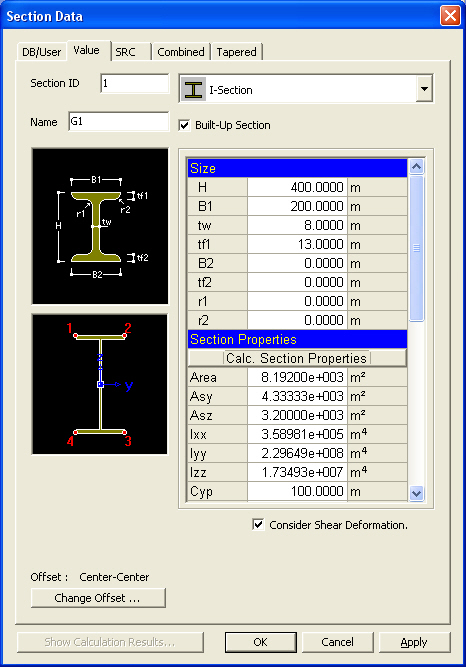
Consider Shear Deformation
Select whether to consider shear deformation.
This option will be applicable for structural analysis, but will not affect
the effective shear areas that appear by clicking
Section Properties
Click Area: Cross sectional area
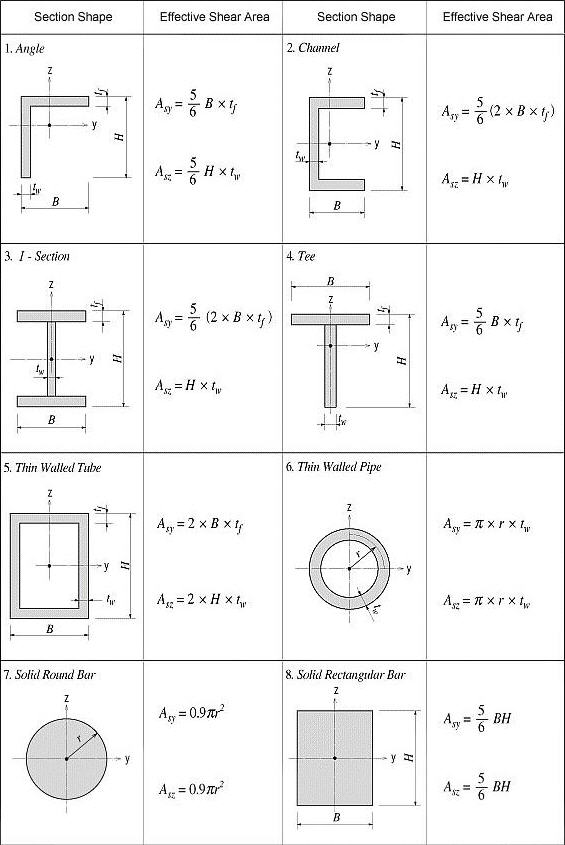
Asy: Effective Shear Area for shear force in the element's local y-direction It becomes inactive when Shear Deformation is not considered.
Asz: Effective Shear Area for shear force in the element's local z-direction It becomes inactive when Shear Deformation is not considered.
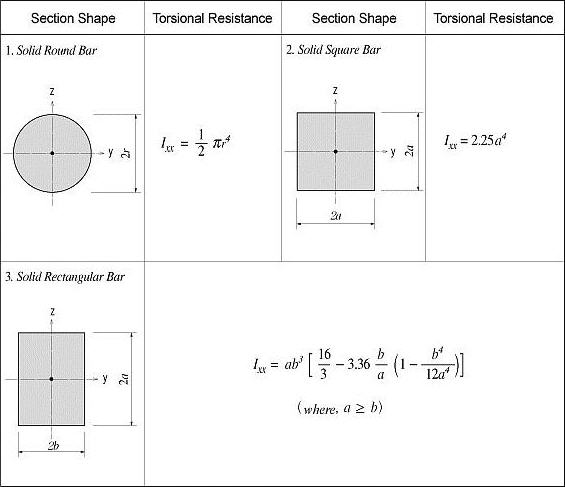
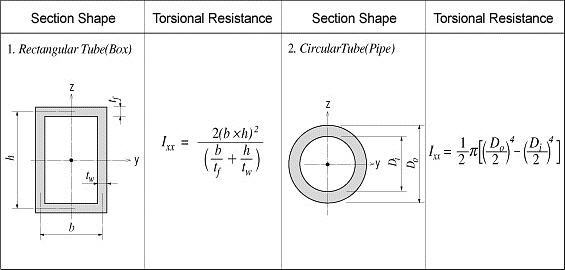
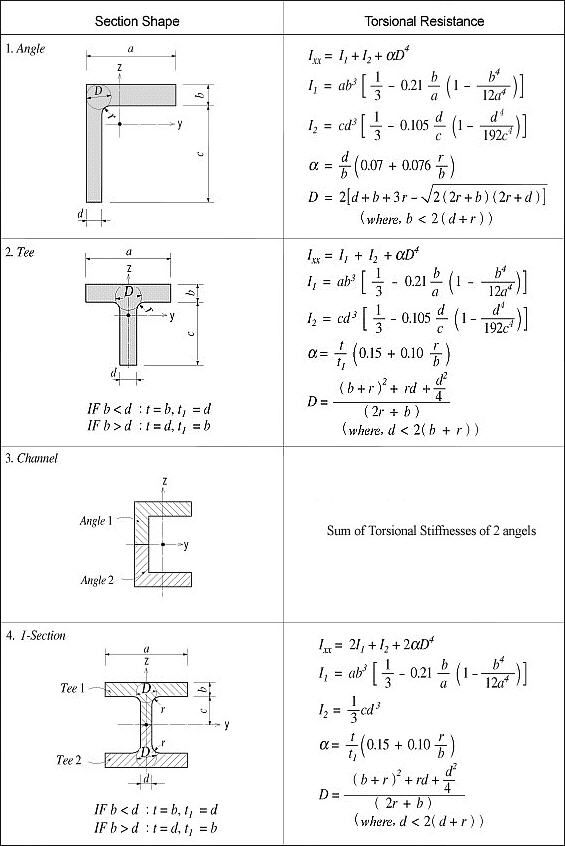
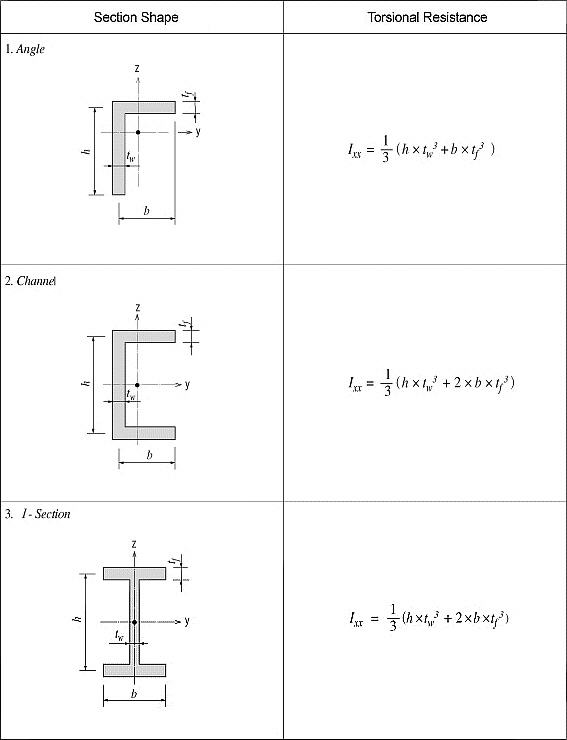
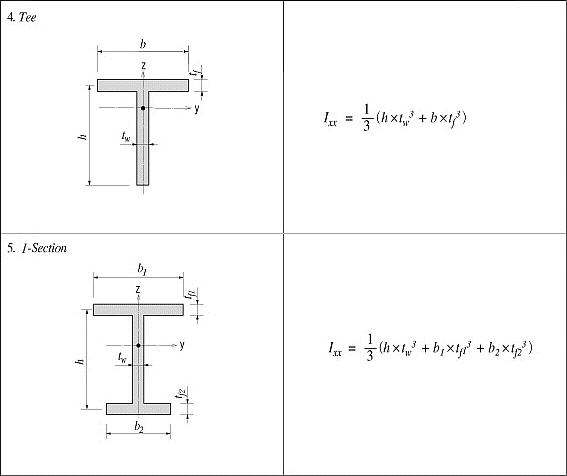
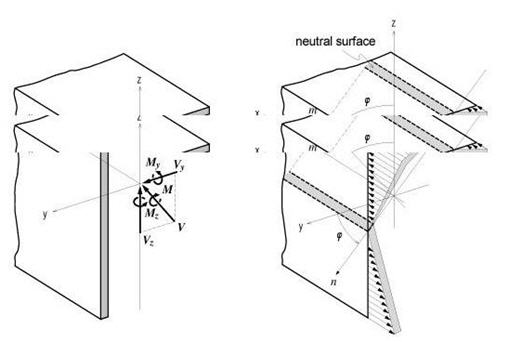
Ixx: Torsional Resistance about the element's local x-axis
Iyy: Moment of Inertia about the element's local y-direction
Izz: Moment of Inertia about the element's local z-direction
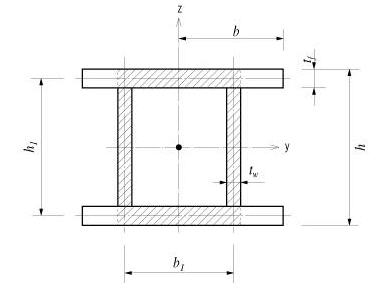
Cyp: Distance from the section's neutral axis to the extreme fiber of the element in the local (+)y-direction
Cym: Distance from the section's neutral axis to the extreme fiber of the element in the local (-)y-direction
Czp: Distance from the section's neutral axis to the extreme fiber of the element in the local (+)z-direction
Czm: Distance from the section's neutral axis to the extreme fiber of the element in the local (-)z-direction
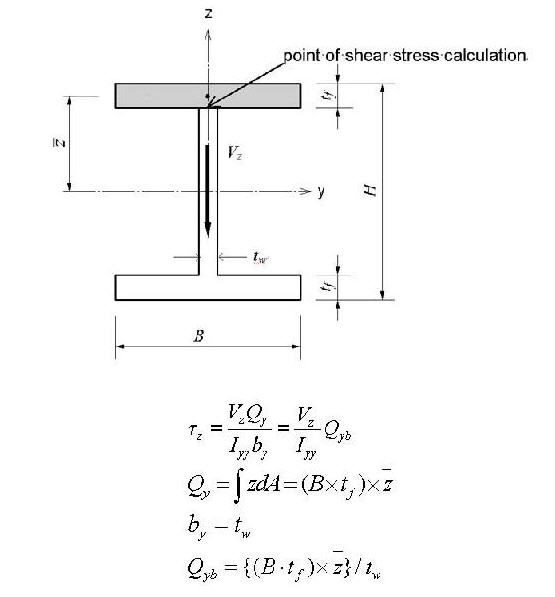
Qyb: Shear Coefficient for the shear force applied in the element's local z-direction
Qzb: Shear Coefficient for the shear force applied in the element's local y-direction
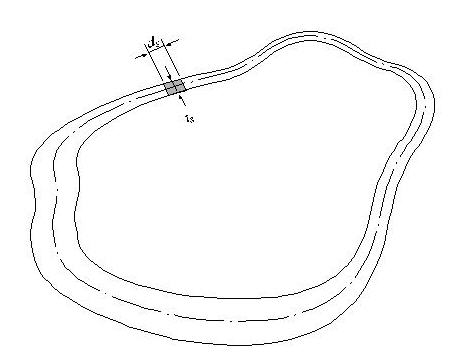
Peri: O: Total perimeter of the section
Peri: I: Inside perimeter length of a hollow section
y1, z1: Distance from the section's neutral axis to the Location 1 (used for computing combined stress)
y2, z2: Distance from the section's neutral axis to the Location 2 (used for computing combined stress)
y3, z3: Distance from the section's neutral axis to the Location 3 (used for computing combined stress)
y4, z4: Distance from the section's neutral axis to the Location 4 (used for computing combined stress)
Zyy: Plastic Section Modulus about the element local y-direction
Zzz: Plastic Section Modulus about the element local z-direction
Note 1 All the above section property data except for Area and Peri are required for beam elements.
Note 2 The shear deformations are neglected if the effective shear areas are not specified. Cyp, Cym, Czp and Czm are used to calculate the bending stresses. Qyb and Qzb are used to calculate the shear stresses. Peri is used to calculate the Painting Area.
Note 3 Zyy and Zzz are used to calculate the strength for pushover analysis when Value Type Steel Section has been assigned Design > Pushover Analysis > Define Hinge Properties.
Note
4 Sections can be defined by the stiffness data entries even if the section dimensions (H, B1, ... , etc.) are not entered.
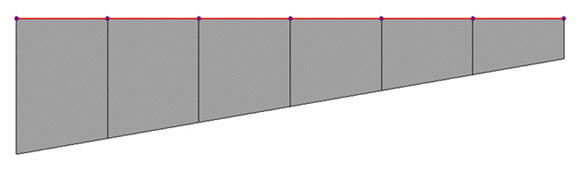
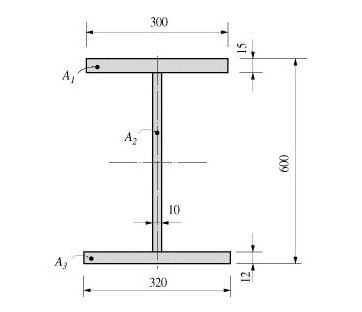
Note 5 Determining the positions of y1~4, z1~4 of a section imported from SPC [Details] 1. Divide the section into four quadrants.
2. Assign the positions furthermost from the centroid in each quadrant for checking stresses.
If the webs of a section are extensively sloped as in the above diagram, the points furthermost from the centroid may not be the lowest points of the section. Use caution that the stress checking positions of quadrants 3 & 4 may be selected differently from the expectation.
Section Type
Revision of V.7.6.1
Section - DB/User dialog box
Section - Value dialog box
Section - SRC dialog box
Section - Combined dialog box
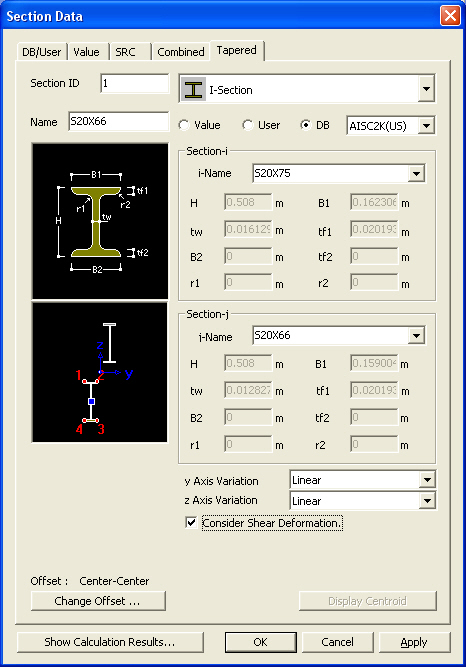
Section - Tapered dialog box
|
|
|
 Section
Section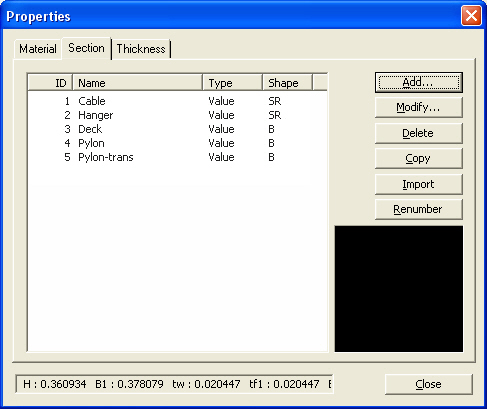
 in the Properties
dialog box and enter the following: Enter the section properties by entry
types.
in the Properties
dialog box and enter the following: Enter the section properties by entry
types. to modify the
related data.
to modify the
related data. .
. .
. and select the MCB
file containing the section data or specify a file name then click
and select the MCB
file containing the section data or specify a file name then click  .
. .
. 
 to
specify a section Offset away from the Centroid. Use
to
specify a section Offset away from the Centroid. Use  Hidden
to verify the input.
Hidden
to verify the input. 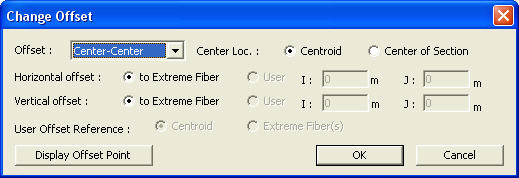

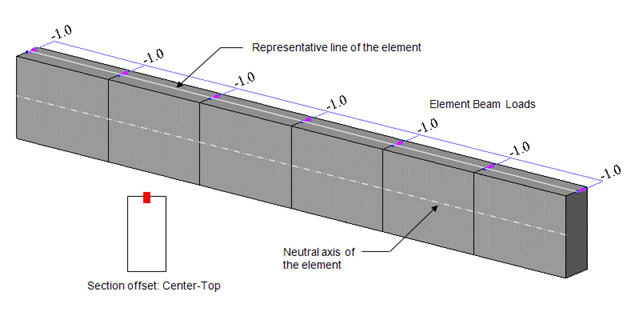
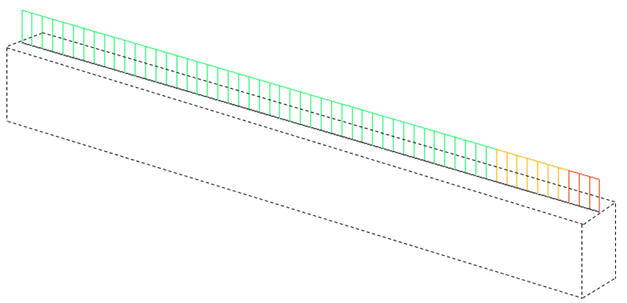
 : Display the Offset specified from the Change Offset dialog
box in the guide diagram of Section Data window.
: Display the Offset specified from the Change Offset dialog
box in the guide diagram of Section Data window.  .
. 
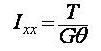
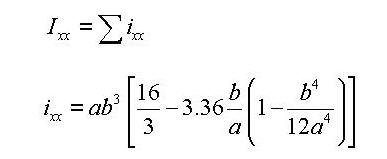
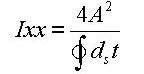
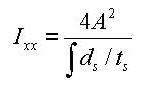
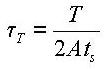
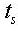
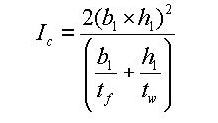

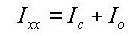
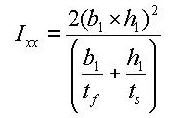

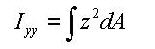
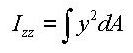
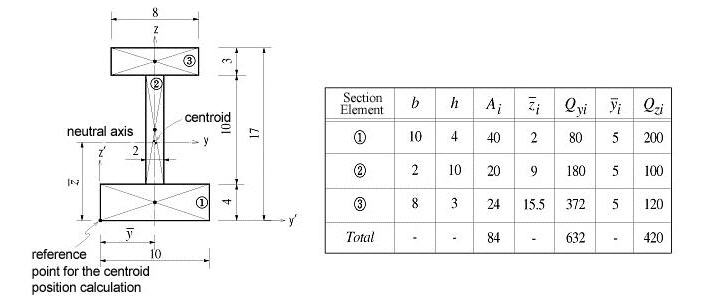
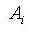 : area
: area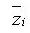 : distance from the reference
point to the centroid of the section element in the z-axis direction
: distance from the reference
point to the centroid of the section element in the z-axis direction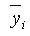 : distance from the reference
point to the centroid of the section element in the y-axis direction
: distance from the reference
point to the centroid of the section element in the y-axis direction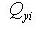 : first moment of area
relative to the reference point in the y-axis direction
: first moment of area
relative to the reference point in the y-axis direction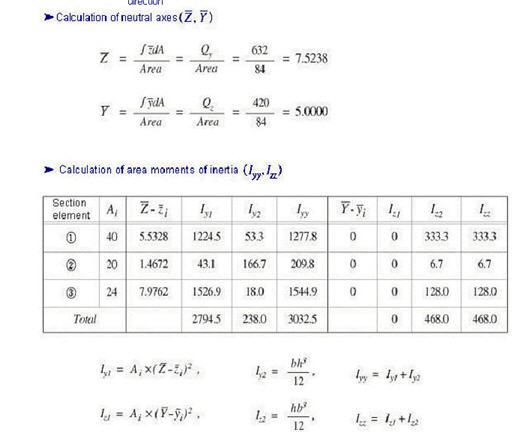
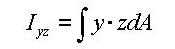
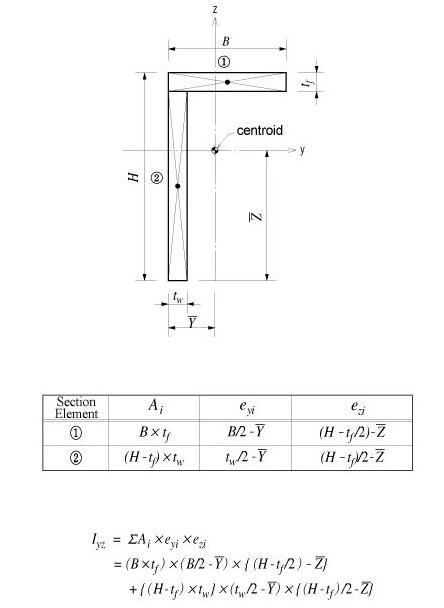
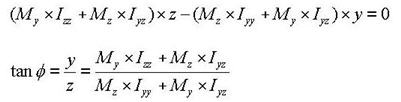
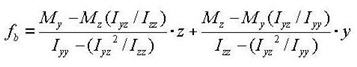
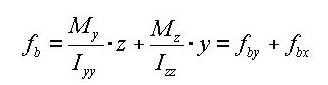
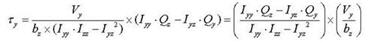
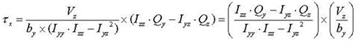
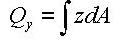
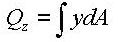
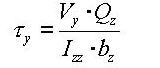
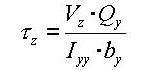
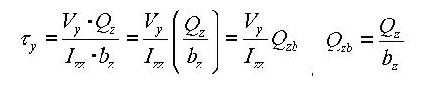

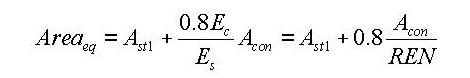
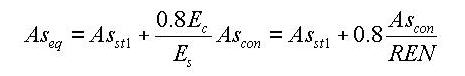
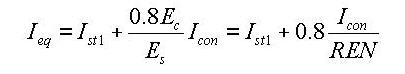
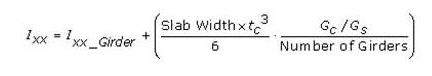


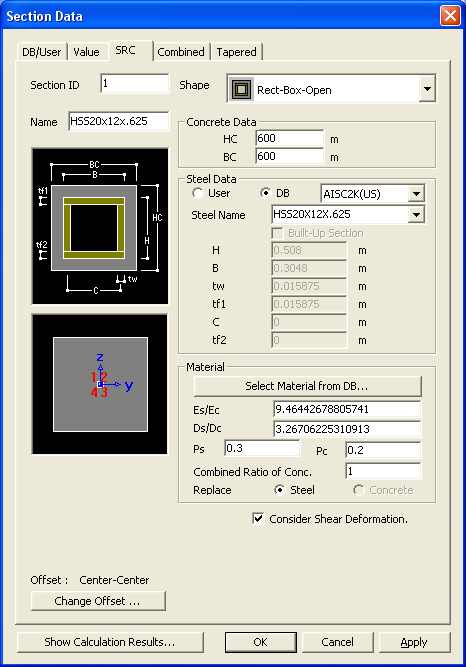
 to select the material
properties for steel and concrete stored in the DB for a country. The
following items are automatically entered:
to select the material
properties for steel and concrete stored in the DB for a country. The
following items are automatically entered: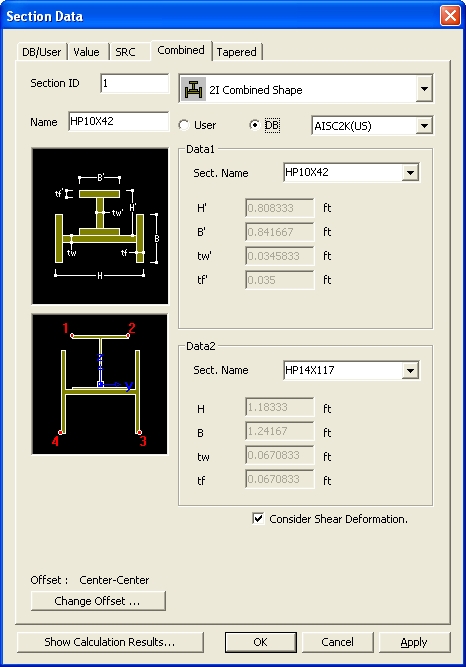



 . Then, the user may modify the
auto-calculated stiffness data or directly enter the stiffness data without
entering the section dimensions.
. Then, the user may modify the
auto-calculated stiffness data or directly enter the stiffness data without
entering the section dimensions.