Revision of Ver.7.4.1

Nonlinear Analysis Control

Specify the iteration method and convergence conditions for performing a nonlinear analysis reflecting large displacement and material nonlinear analysis . The large displacement analysis can be applied to both general static analysis and construction stage analysis. Material nonlinear analysis can only be applied to static analysis. Prior to an analysis, specify the sequence of applying loads in Loading Sequence for Nonlinear Analysis, and define the convergence criteria for nonlinear analysis in Nonlinear Analysis Control. Specified loading sequence is effective only when Newton-Raphson is selected as the Iteration Method. Large displacement analysis and material nonlinear analysis can be performed on Truss, Plate, Plane Stress, Plane Strain, Axisymmetric, and Solid elements.

Note

Tension-only/Compression-only element will be changed to Truss element in Eigenvalue Analysis.

From the Main Menu select Analysis > Nonlinear Analysis Control.

Nonlinear Analysis Control dialog box

 

Nonlinear Type

Select a type of nonlinear analysis

Geometry Nonlinear: Geometric large displacement nonlinear analysis

Material Nonlinear: Material plasticity static analysis

Revision of Ver.7.4.1

 

Note 1

Following elements can be used in geometry nonlinear analysis and/or material nonlinear analysis

 

Element

Geometry Nonlinear

Geometry Nonlinear

(Initial Force for Geometric Stiffness)

Material Nonlinear

Truss

O

O

O

Tension only

O

O

O

Hook

O

O

O

Cable

O

O

ツ

Compression only

O

O

O

Gap

O

O

O

Beam

O

O

ツ

Plate – Thick

O

ツ

O

Plate – Thin

ツ(Considered as Thick Plate)

ツ

ツ (Considered as Thick Plate)

Plane Stress

O

ツ

O

Plane Strain

O

ツ

O

Axisymmetry

O

ツ

O

Solid

O

ツ

O

 

(O : Analysis can be performed. / X : Analysis cannot be performed. / ≠ : Corresponding elements are considered as linear elements and then analysis can be performed.)

 

Note 2

Geometry nonlinear analysis and/or material nonlinear analysis cannot be performed for the items marked ／.

 

 

Limitation

Geometry Nonlinear

Material Nonlinear

Material + Geometry Nonlinear

Remark

Beam End Release

x

O*

x

 

Plate End Release

x

O*

x

 

Pretension Load

O

x

x

 

Prestress Load

O

x

x

 

CInitial Forces for Geometric Stiffness

O

x

x

 

Temperature Loads

O

x

x

 

Material=SRC

x

x

x

 

 

 

 

In case of Beam End Release and Plate End Release, the material nonlinear analysis cannot be performed for the following case:

 

1) When Load > Nonlinear Analysis > Loading Sequence for Nonlinear Analysis is used

 

Note 3

Analysis result is produced only at both I & J ends of elements in geometry nonlinear analysis.

Iteration Method

Select the method of iteration.

If Newton-Raphson is selected

Number of Load Steps
Divide the total load into the number of Load Steps and apply the loads by each step.
 

Maximum Number of Iterations/Load Step
Maximum number of iterations of analysis per Load Step.

If Arc-Length is selected

Number of Increment Steps

Maximum Number of Iterations/Increment Step
Maximum number of iterations of analysis per Increment Step.

Maximum Displacement Boundary
Magnitude of maximum displacement

Initial Force Ratio for Unit Arc-Length (%)

Ratio of the Initial Force per Unit Arc-Length

 

Note

Real number (decimal) can be input

If Displacement-Control is selected

Number of Displacement Steps
Divide the total displacement into the number of Displacement Steps and apply the incremental displacement by each step.

Maximum Number of Iterations/Increment Step
Maximum number of iterations of analysis per Increment Step

Master Node
A reference node for displacement control

Direction
Direction of the displacement control

Maximum Displacement
The magnitude of maximum displacement to be applied to analysis

 

Convergence Criteria

Specify the basis on which to assess the convergence.

Energy Norm
Assess the convergence on the basis of Energy (Member force x displacement) Norm.

Displacement Norm
Assess the convergence on the basis of Displacement.

Force Norm
Assess the convergence on the basis of Member Force Norm.

Note
The selection of the convergence criteria for repeating or ending the analysis must be based on the condition to reflect the effects of various degrees of freedom. For example, in the case of Displacement Norm, if the displacement resulting from the corresponding analysis step is {D1}, and the total displacement accumulated from each step is {D2}, the Norm is expressed as . If this value is smaller than the specified value, a convergence is considered to have occurred and the program stops the iterative analysis.

 

: Remove the conditions for a nonlinear analysis.

 

Load Case Specific Nonlinear Analysis Control Data

The above defined Iteration Method is applied individually by load cases. If the same iteration method is applied to all the load cases, this dialog box need not be used.

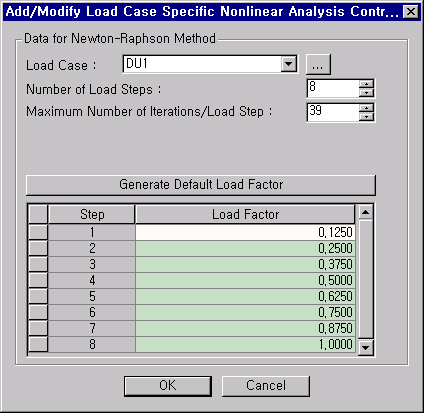
Load Case Specific Nonlinear Analysis Control Data dialog box

Data for Newton-Raphson/Arch-Length/Displacement-Control Method
Title of Iteration Method specified

Step: Number of Load Steps entered

Load Factor: load factors for each increment, which can be user-defined or auto-generated by clicking on the Generation button.

8 steps are generated in the Dialog box above in accordance with the Number of Load Steps entered.

Load Factors can be user-difined, or auto-generated by clicking on the button.

Note

When Arc-Length Method (ALM) is used to solve the nonlinear equilibrium equation, a real number can be inputted into the “Initial Force Ratio for Unit Arc-Length (%)” text box in Nonlinear Analysis Control.