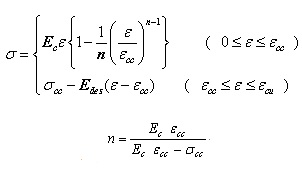ファイバー要素の材料の定義
ファイバー用を用いた非弾性時刻歴解析を行うために鉄筋とコンクリートの応力-ひずみ関係を定義します。
各モデルは提案者の示方規定によって異なります。
リボンメニュー : モデル > 材料 & 断面 > 非線形特性 > ファイバー要素の材料
ツリーメニュー : メニュータブ > モデリング > 材料&断面 > ファイバー要素の材料
 ファイバー要素の材料の定義
ファイバー要素の材料の定義
梁要素の断面を小さなファイバーに分割して各ファイバーセルが特定の応力-ひずみ関係を持つようにします。
ファイバー材料に対する特性を定義します。
 名称
名称
ファイバー要素の名前
 材料タイプ
材料タイプ
履歴モデルを定義する材料を選択します
 履歴ループタイプ
履歴ループタイプ
履歴モデルを定義する材料を選択します。
 参照材料
参照材料
各モデルによる挿図を参考し、材料の履歴挙動に関するスケルトン曲線の特性値を入力します。
■ コンクリート
 Kent & Park モデル
Kent & Park モデル
Modified Kent & Park Concrete モデルで、横拘束効果(Confinement Effect)等を考慮できます。
Kent and Park(1973)の基本モデルをScott et al.(1982)などが修正したモデルであり、
正確な解析ができるモデルとして良い評価をされている。
f'c : コンクリート圧縮強度
K : 拘束効果による圧縮強度の増加効果を表現する係数
ε_cu : 圧縮Crushing発生時のひずみ
ε_c0 : 最大圧縮強度発現時のひずみ
Z : 圧縮降伏以後、コンクリートの軟化区間の剛性を表すための係数
 コンクリート標準示方書モデル
コンクリート標準示方書モデル
日本コンクリート標準示方書[耐震性能調査編, p23]のモデルで最大応力点を超えた軟化領域と残留塑性変形、
除荷再載荷時の剛性低下効果を反映しています。
fc' : コンクリートの最大圧縮強度
ε'_peak : 最大圧縮強度発現時のひずみ
Note
 日本道示V(H14/24)モデル
日本道示V(H14/24)モデル
日本道路橋示方書同解説、V耐震設計編[鉄筋拘束コンクリート、p.161]のモデルです。
地震動の種類により応力‐ひずみの関係が異なります。
本モデルは地震動と拘束鉄筋による影響、断面形状などの影響を反映しています。
地震タイプ Ⅰ 地震タイプⅡ
地震 タイプ I : 極限ひずみと最大圧縮強度時のひずみが同じになって下降勾配(Edes)区間を持っていません。
つまり、圧縮ひずみが最大圧縮強度に達つと、すぐにCrushingが生じると見なせます。
地震タイプ II : 極限ひずみは示方規定式によって算定され、下降勾配(Edes)区間を持ちます。
Ec : コンクリートのヤング係数
σ_ck : コンクリートの設計基準強度
σ_sy : 横拘束鉄筋の降伏点
α, β : 断面補正係数
Note
円形断面の場合にはα=1.0, β=1.0
梯形断面、中空円形断面及び中空梯形断面ではα=0.2, β=0.4
A_h : 横拘束鉄筋1本当たりの断面積
s : 横拘束の間隔
d : 横拘束の拘束長で、帯筋や中間帯筋によって分割拘束された内部コンクリートの辺の中で一番長い辺の長さにする。
σ_bt : コンクリートの引張強度
σ_cc : 横拘束鉄筋で拘束されたコンクリートの強度
 名古屋高速公社モデル
名古屋高速公社モデル
名古屋高速公社(名高社)のモデルとして、[コンクリートを部分的に充填した剛性橋脚の耐震性能調査(案) p.7]のモデルです。
σ_ck : コンクリートの圧縮強度
ε_cc : コンクリートの圧縮強度到達時のひずみ
K : 圧縮強度増加を反映するための係数
ε_cu : コンクリートの極限圧縮ひずみ
ε_t0 : コンクリートの最大引張強度発現しのひずみ
ε_t1 : コンクリート引張破壊発生時のひずみ
ε_tu : コンクリートの極限引張ひずみ
 トリリニアモデル
トリリニアモデル
引張部と圧縮部両方を定義できるモデルであり、圧縮部はトリリニア履歴を持ちます。トリリニア履歴を定義するための
応力-ひずみで入力する方式と応力-剛性低減率で入力する方式の2つの方式があります。
応力‐ひずみ 定義方式 応力‐剛性低減率 定義方式
σ_c1 : コンクリートの1次圧縮降伏強度
σ_c2 : コンクリートの2次圧縮降伏強度
σ_c3 : コンクリートの2次圧縮降伏以後の強度(K3算定時に必要)
ε : コンクリートの最大引張強度発現時のひずみ
ε_t1 : コンクリート引張破壊発生時のひずみ
ε_tu : コンクリートの極限引張ひずみ
ε_c1 : コンクリートの1次圧縮降伏ひずみ
ε_c2 : コンクリートの2次圧縮降伏ひずみ
ε_c3 : コンクリートの2次圧縮降伏以後のひずみ(K3算定時に必要)
ε_cu : コンクリートの3次圧縮降伏ひずみ
K1 : コンクリートの初期剛性
K2/K1 : コンクリートの1次降伏後の剛性と初期剛性の比
K3/K1 : コンクリートの2次降伏後の剛性と初期剛性の比
ε_cu : コンクリートの3次圧縮降伏ひずみ
引張強度を超えた後、下降区間での剛性で実際履歴の傾きを用いる方式もあります。
しかし、この値は負数のため、極限状態で修練効率性を落とす可能性があるので、E=1.d-15で設定されています。
Note
'σ - ε'入力方式で、ε_c1~ε_c3を入力した状態で、'σ - α'入力方式を選択すると自動で
剛性K1, K2/K1, K3/K1を計算してくれます。その逆も自動で計算されます。
 Mander モデル
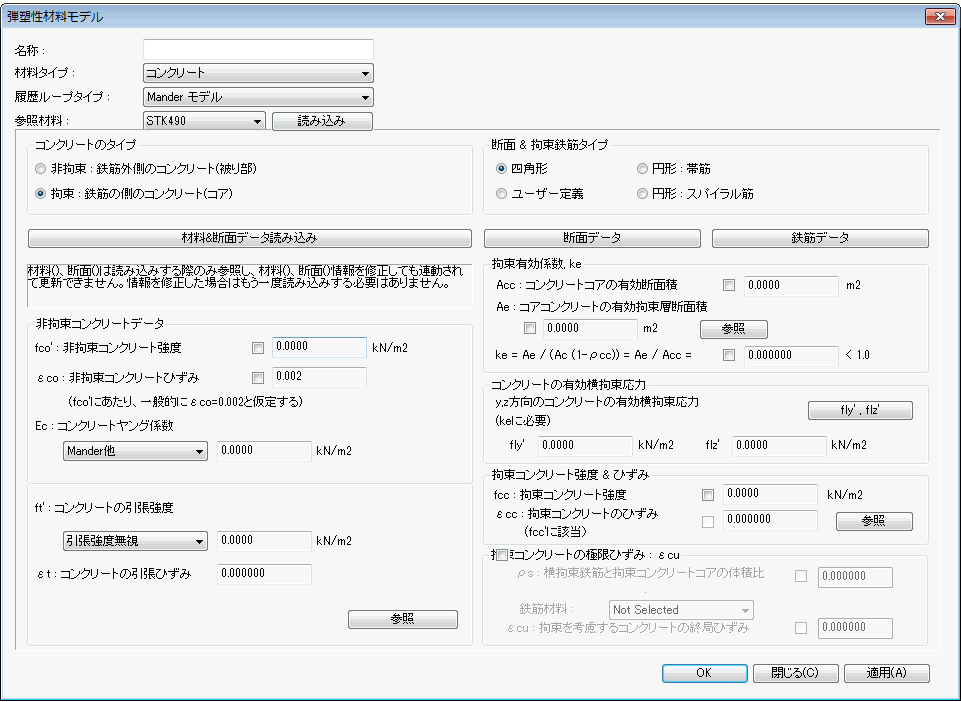
Mander モデル
特徴
横拘束鉄筋により拘束された圧縮コンクリートについてMander(1988)が提案してモデルです。
横拘束鉄筋はコンクリートの拘束効果のみではなく、主筋の座屈を防止し、せん断破壊を防止します。
横拘束鉄筋により拘束された圧縮コンクリートは横拘束効果により強度と粘性を大きく増加させる効果があります。
Manderモデルは拘束された圧縮コンクリートの応力度‐変形度の関係を提案したモデルであり、コンクリートの断面形状に構わず適用できます。
更に、縦方向鉄筋及び拘束鉄筋の量、拘束鉄筋の降伏強度と配筋形態を考慮してコンクリートの拘束力である有効拘束応力を算定できます。
ManderモデルはPopovic(1973)が提案した1軸応力度‐変形度関係を用いるが、
多軸の効果を考慮した有効拘束力を同価の1軸応力‐ひずみ関係で取り替える方法を使用しています。
制限事項
Mander Modelはコンクリートの断面形状に構わず適用できます。ただし、材料データと断面データのImportによる強度自動算定は円形、
四角形断面のみ支援し、円形、四角形断面以外の断面については強度児童計算に必要な情報をユーザーが入力すれば自動計算による
強度が得られます。
■ Steel
 Menegotto-Pintoモデル
Menegotto-Pintoモデル
Menegotto and PintoのSteelモデルをFilippouなどが修正したモデルです。
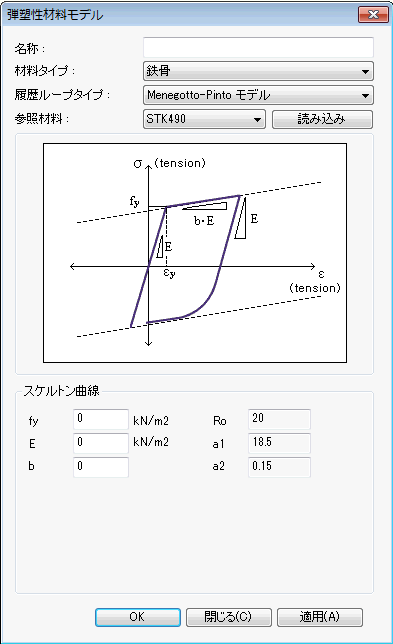
f_y : 鉄筋の降伏強度
E : 鉄筋の初期剛性
b : 降伏後、鉄筋の剛性と初期剛性の比
R0, a1, a2 : 降伏後、鉄筋の応力-ひずみ曲線挙動状態を定義する常数
 バイリニアモデル
バイリニアモデル
一般的な対称バイリニア(Bilinear)鉄筋モデルです。
f_y : 鉄筋の降伏強度
E1 : 鉄筋の初期剛性
E2/E1: 降伏後の鉄筋の剛性と初期剛性の比
下の図のよう、降伏後の除荷(Unloading)、再載荷(Reloading)時には弾性剛性で挙動します。
![]() バイリニアモデル(バウシンガー効果考慮)
バイリニアモデル(バウシンガー効果考慮)
一般的なバイリニア型鉄筋モデルを発展させたモデルとして、降伏後の鉄筋の剛性を任意で定義できるし、
鉄筋の座屈と破断などを考慮できます。
σ_y : 引張側圧縮強度
σ_cy : 圧縮側圧縮強度
ε1 : 鉄筋の圧縮座屈発生時のひずみ
ε2 : 引張降伏後の鉄筋破断発生時のひずみ
E1 : 鉄筋の初期剛性
E2 : 引張降伏後の鉄筋の剛性
E3 : 載荷時に鉄筋の降伏以後の剛性
E4 : 圧縮降伏以後の鉄筋の剛性(?-?値を指定すると負勾配を考慮することができます。)
E5 : 圧縮降伏が発生した鉄筋の座屈以後の剛性
 トリリニアモデル
トリリニアモデル
3つの勾配を持つトリリニアモデルとして、履歴入力を応力-ひずみの座標で入力する方式と剛性の低減率で
入力する方式の2つがあります。
除荷、再載荷時の弾性剛性を基に挙動します。
σ1y : 引張側1次降伏強度
σ2y : 引張側2次降伏強度
σ3y : 引張側2次降伏後強度(K3算定時に必要)
σ'1y : 圧縮側1次降伏強度
σ'2y : 圧縮側2次降伏強度
σ'3y : 圧縮側2次降伏後強度(K5算定時に必要)
ε1y : 引張側1次降伏ひずみ
ε2y : 引張側2次降伏ひずみ
ε3y : 引張側2次降伏後ひずみ(K3算定時に必要)
ε'1y : 圧縮側1次降伏ひずみ
ε'2y : 圧縮側2次降伏ひずみ
ε'3y : 圧縮側2次降伏後ひずみ(K5算定時に必要)
K : 鉄筋の初期剛性
K2/K1 : 1次引張降伏後の鉄筋の剛性と初期剛性の比
K3/K1 : 2次引張降伏後の鉄筋の剛性と初期剛性の比
K4/K1 : 1次圧縮降伏後の鉄筋の剛性と初期剛性の比
K5/K1 : 2次圧縮降伏後の鉄筋の剛性と初期剛性の比
Note
'σ - ε'入力方式で、ε1y~ε'3yを入力した状態で、'σ - α'入力方式に変換すると自動でそのひずみに該当する
剛性K1, K2/K1, K3/K1を計算してくれます。その逆も自動で計算されます。
 Parkモデル
Parkモデル
Kent & Park(1973)により行われた反復荷重を与えられる軟鋼の弾性区間、塑性区間と変形度‐硬化(Strain Hardening)区間の模写が可能であり、
Ramberg-Osgood式によるBauschinger Effectを詳しく表して実験的な結果と高い一致性が得られるモデルです。
fy:鉄骨の降伏強度
fu:鉄骨の終局強度
Es:鉄骨のヤング係数
εy:鉄骨の降伏ひずみ
εsh:ひずみ硬化開始点ひずみ
εsu:鋼材の破断ひずみ