|
Sekiguchi-Ohta 재료 모델의 Viscid 타입은 지반의 크리프(creep) 거동을 모사하기 위한 다양한 점소성 이론 중에서, 비정상성 흐름면 이론(nonstationary flow surface theory) 을 따르는 모델입니다. 비정상성 흐름면 이론의 모델은 기본적으로 소성 모델에 근간을 두고 있지만, 시간 종속(time dependent)성을 지닌 함수를 포함하고 있다는 차이점이 있습니다. Viscid 타입에서, 초기 상태의 지반은 하중이 적용되기 이전에 일정한 응력 상태로 크리프(creep)이 진행되고 있다는 가정을 따릅니다.
비선형 파라미터는 Inviscid 와 동일하고, 시간종속 파라미터를 추가로 입력 받습니다. Viscid 타입의 흐름 함수(flow function)은 다음과 같이 표현됩니다.
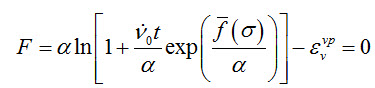
여기서
|
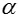 : :
|
: 과압밀선 기울기
|
|
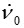
|
: 한계상태선 기울기
|
|
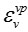
|
: 정규압밀 응력비
|
[주요 파라미터]]
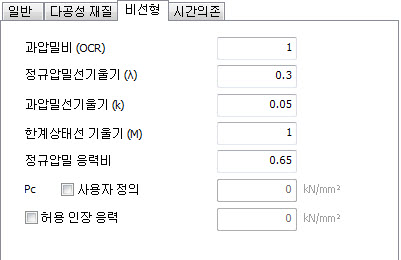
|
기호
|
항목
|
설명
|
|
비선형
|
|
λ
|
정규압밀선의 기울기
|
Cc / 2.303
|
|
κ
|
과압밀선 기울기
|
Cs / 2.303
(Cc/5 개략적인 추정값)
|
|
M
|
한계상태선 기울기
|
6 x sinФ’ / (3-sinФ’)
(Ф’ : 내부마찰각)
|
|
KOnc
|
정규압밀 응력비
|
1-sinФ’ (<1)
|
|
캡 항복면
|
|
OCR/Pc
|
과압밀비/선행압밀하중
|
두 개의 값을 동시에 입력하는 경우, Pc 값이 우선 고려됩니다.
|
|
Tallow
|
허용인장응력
|
참고
|
|
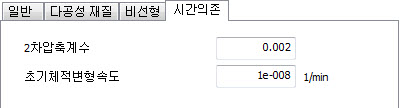
시간의존
|
|
a
|
2차 압축계수
|
Cc/20 (개략적인 추정값)
|
|
V0
|
초기체적 변형속도
|
참고
|
|
t0
|
1차압밀 종료시간
|
참고
|
참고 : Sekiguchi - Ohta 모델의 파괴기준은 인장응력의 발생을 허용하지 않습니다. 하지만, 다양한 조건에서 인장응력이 발현될 수 있기 때문에(예 : 성토로 인해 발생하는 인접 지반의 융기)이러한 재료모델의 한계를 극복하기 위해 ‘허용 인장응력’의 범위를 설정할 수 있습니다.
적절한 ‘허용 인장응력’의 값을 얻기 위해서는 반복해석을 통해, 성토하중이나 지반 파괴로 인해 발생하는 인장응력 값 보다 큰 값을 입력해야 합니다. 하지만, 선행압밀하중을 고려하는 경우, 허용 인장응력은 선행압밀하중 값을 초과할 수 없습니다. 선행압밀하중 값은 OCR 값으로부터 자동 계산되며 초기에 입력된 허용인장응력 값을 고려하여 계산됩니다.
참고 : 시간의존
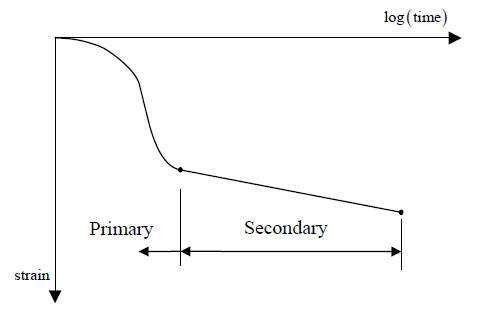 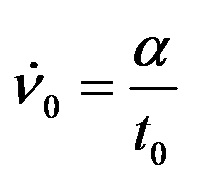
<로그 시간에 따른 1차, 2차 압밀 곡선>
|


