Story Shear Force Ratio
▒ 기능
|
" Model > Building > Control Data"에서 "Story Shear Force Ratio" 의 “Consider Story Module”을 Check On을 했을 경우 중복층의 전단력에 대한 정확한 결과를 얻을 수 있습니다. Results > Result Tables > Story > Define Module에서 모듈을 정의한 경우에 테이블의 첫 번째 Column에 Module이 생성됩니다. 본기능은 " Model > Building > Control Data"에서 "Story Shear Force Ratio" 를 반드시 Check 해야하며 Default값으로 Check 되어 있습니다. Note 분배율은 기둥 부재(Frame_Beam)와 브레이스 부재(Frame_Truss), 전단벽부재(Wall)가 저항하는 비율로 표현됩니다. Note
|
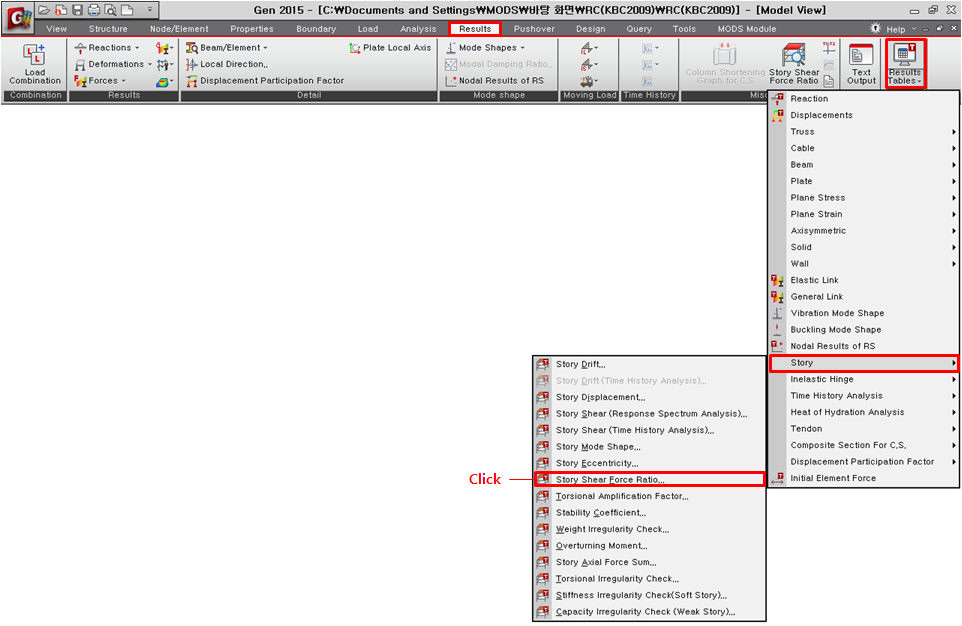
▒ 호출
|
|
▒ 입력
|
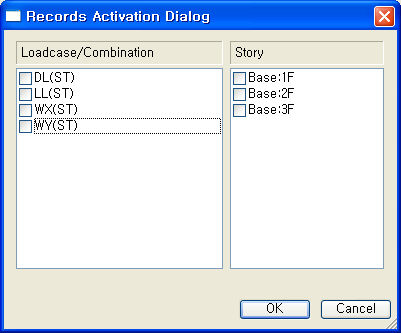
Active Dialog에서 층전단력의 확인을 원하는 시간이력 하중조건을 선택합니다.
Record Activation 대화상자
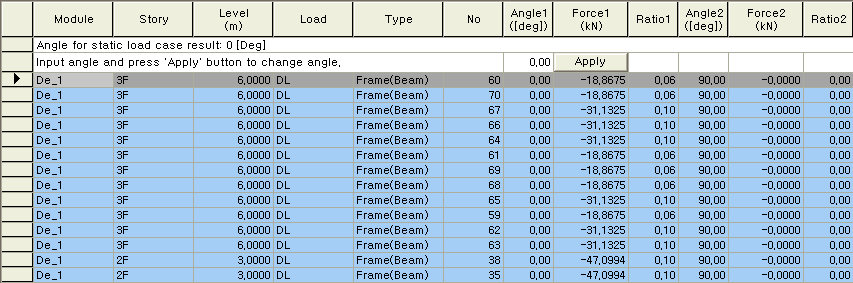
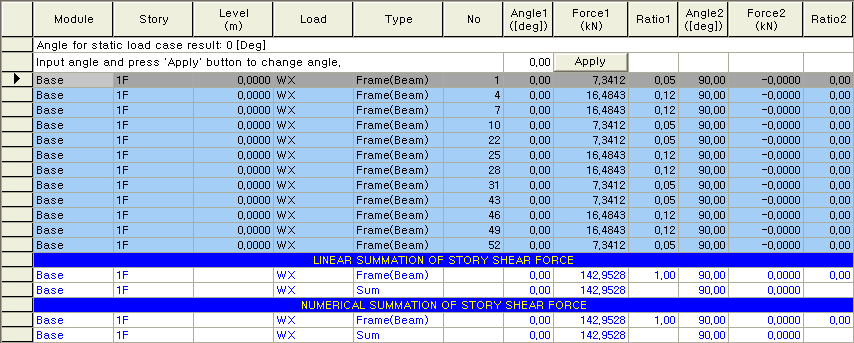
Story : 층 이름 Level : 층 높이 Load : 정적수평하중(정적지진하중, 풍하중) Type : 요소 종류 Frame(Beam) : 기둥부재 Frame(Truss) : 브레이스부재 Wall : 전단벽부재 Note 해당됩니다. No : 요소 번호 Angle1([deg]) : 요소별 전단력 계산의 기준각도 Force1(tonf) : 해당 요소가 Angle1 방향으로 분담하는 전단력 Ratio1 : Angle1 방향으로 층전단력에 대한 해당 요소가 분담하는 전단력의 비율 Angle2([deg]) : Angle1 + 90도 Force2(tonf) : 해당 요소가 Angle2 방향으로 분담하는 전단력 Ratio2 : Angle2 방향으로 층전단력에 대한 해당 요소가 분담하는 전단력의 비율 Input angle and press 'Apply' button to change angle : 해당 요소가 분담하는 전단력의 각도(Angle1)를 입력한후, LINEAR SUMMATION OF STORY SHEAR FORCE : 해당 각 층에 대하여 Frame, Wall 각각에 대한 전단력을 단순하게 더한 결과를 출력 NUMERICAL SUMMATION OF STORY SHEAR FORCE : 모든 요소의 전단력을 모드별로 더한 후 조합한 결과를 출력 Note 하중과 층전단력이 일치하게 되며, 그 때의 각 부재별 전단력 분담 비율을 확인할 수 있다.
Note - LINEAR SUMMATION 과 NUMERICAL SUMMATION의 차이와 활용 전단력을 더한 후 각각의 비율을 출력하는 테이블이다. 따라서, 응답스펙트럼 해석에 대한 밑면전단력은 요소에 대한 전단력을 모드별로 조합한 결과이므로 따라서 최하층의 전단력을 밑면전단력으로 사용할 수 없다. 해당 층의 Frame(F)과 Wall(W)부재들의 전단력 합과 해당 층의 전단력합(F+W)의 비율을 출력, 이때 부재별 전단력은 응답스펙트럼 모드별 조합을 수행한 후의 값을 사용한다. 따라서, 응답스펙트럼 해석에 대한 밑면전단력은 요소에 대한 전단력을 모드별로 조합한 결과이므로 Linear Summation에서 출력되는 출력되는 최하층의 전단력을 밑면전단력으로 사용할 수 없다.
b. NUMERICAL SUMMATION : 이 테이블은 각 층에 대한 Frame과 Wall의 전단력 비율을 출력함과 동시에 해당층에 대한 전단력을 출력하는 테이블이다. 따라서, 층전단력 비율이 1.0이 되지 않는 경우가 일반적이다. 따라서, 동적밑면전단력과 정적밑면전단력의 비(Scale Factor)를 구할 경우 이 테이블의 최하층에서 출력되는 전단력을 이용하여 계수를 산출할 수 있다. 해당 층의 Frame(F)과 Wall(W)부재들의 전단력 합과 해당 층의 전단력합(F+W)의 비율을 출력, 이때 해당 층의 Frame(F)과 Wall(W) 부재들의 전단력 합은 먼저 모드별로 계산하고 이를 응답스펙트럼의 조합방법에 따라 조합한 값을 사용한다. 따라서, 응답스펙트럼 해석에 대한 밑면전단력은 Numerical Summation에서 출력하는 값을 이용해야 한다.
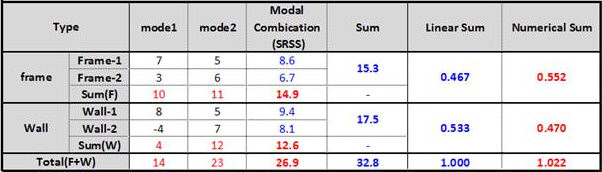
c. LINEAR SUMMATION와 NUMERICAL의 차이 : 아래 표를 통해 예를들면 다음과 같다. Linear Summation은 해당층의 부재들의 전단력의 합을 SRSS조합의 방법으로 구하고, 그 값들을 단순하게 합한 값에 대한 비율을 구한다. 즉, 표에서 해당층의 Frame1과 Frame2의 전단력의 합은 SRSS조합의 방법으로 구한 값으로 각각 8.6(√(7^2+5^2)), 6.7(√(3^2+6^2))이고 frame의 전단력의 합은 두 개를 단순히 더한 값인 15.3이다. Wall도 마찬가지로 Wall-1과 Wall-2의 전단력의 합은 각각 9.4((√(7^2+5^2)), 6.7(√(3^2+6^2))이고 Wall의 전단력의 합은 17.5이다. Frame과 Wall의 Sum의 값 15.3과 17.5를 단순하게 더한 값인 32.8(15.3+17.5)이 해당층의 모든 부재에 대한 Sum의 값으로 이에 대한 Frame과 Wall의 비율이 각각 0.467(15.3/32.8)과 0.533(17.5/32.8)이며 비율의 합은 항상 1이 된다. 이것이 Linear Summation이다. Numerical Summation은 모드별로 해당층의 부재들의 전단력의 값들을 단순하게 더한 값을 구하고, 그 값들을 SRSS조합의 방법으로 각각 계산하여 비율을 구한다. 즉, 표에서 해당층의 모드별(mode1과 mode2) frame 부재의 전단력의 단순합은 각각 10(7+3), 11(5+6)이고, SRSS조합의 방법으로 frame의 전단력의 합을 구하면 14.9(√(10^2+11^2))가 된다. Wall도 동일한 방법으로 구하면 mode1, mode2의 단순합은 각각 4(8-4), 12(5+7)이고, Wall의 전단력의 합은 12.6((√(4^2+12^2))이 된다. 여기서 해당층 모든 부재에 대한 총합은 단순히 14.9와 12.6을 더하는 것이 아니라 각 부재의 모드별 값을 더한 값에 대해 SRSS조합의 방법으로 구하는 것으로 모드별 frame과 Wall의 합인 14(10+4)와 23(11+13)을 SRSS조합의 방법으로 구한 26.9((√(14^2+23^2))가 된다. frame과 Wall의 비율은 각각 0.552(14.9/26.9) 와 0.470(12.6/26.9)이 된다. 이것이 Numerical Summation이다.
Module : 모듈 이름 Story : 층 이름 Level : 층 높이 Load : 정적수평하중(정적지진하중, 풍하중) Type : 요소 종류 Frame(Beam): 기둥부재 Frame(Truss): 브레이스부재 Wall : 전단벽부재 Note 해당됩니다. No : 요소 번호 Angle1([deg]) : 요소별 전단력 계산의 기준각도 Force1(tonf) : 해당 요소가 Angle1 방향으로 분담하는 전단력 Ratio1 : Angle1 방향으로 층전단력에 대한 해당 요소가 분담하는 전단력의 비율 Angle2([deg]) : Angle1 + 90도 Force2(tonf) : 해당 요소가 Angle2 방향으로 분담하는 전단력 Ratio2 : Angle2 방향으로 층전단력에 대한 해당 요소가 분담하는 전단력의 비율 Input angle and press 'Apply' button to change angle : 해당 요소가 분담하는 전단력의 각도(Angle1)를 입력한후, Note 하중과 층전단력이 일치하게 되며, 그 때의 각 부재별 전단력 분담 비율을 확인할 수 있다.
Note - LINEAR SUMMATION 과 NUMERICAL SUMMATION의 차이와 활용 전단력을 더한 후 각각의 비율을 출력하는 테이블이다. 따라서, 응답스펙트럼 해석에 대한 밑면전단력은 요소에 대한 전단력을 모드별로 조합한 결과이므로 따라서 최하층의 전단력을 밑면전단력으로 사용할 수 없다. 해당 층의 Frame(F)과 Wall(W)부재들의 전단력 합과 해당 층의 전단력합(F+W)의 비율을 출력, 이때 부재별 전단력은 응답스펙트럼 모드별 조합을 수행한 후의 값을 사용한다. 따라서, 응답스펙트럼 해석에 대한 밑면전단력은 요소에 대한 전단력을 모드별로 조합한 결과이므로 Linear Summation에서 출력되는 출력되는 최하층의 전단력을 밑면전단력으로 사용할 수 없다.
b. NUMERICAL SUMMATION : 이 테이블은 각 층에 대한 Frame과 Wall의 전단력 비율을 출력함과 동시에 해당층에 대한 전단력을 출력하는 테이블이다. 따라서, 층전단력 비율이 1.0이 되지 않는 경우가 일반적이다. 따라서, 동적밑면전단력과 정적밑면전단력의 비(Scale Factor)를 구할 경우 이 테이블의 최하층에서 출력되는 전단력을 이용하여 계수를 산출할 수 있다. 해당 층의 Frame(F)과 Wall(W)부재들의 전단력 합과 해당 층의 전단력합(F+W)의 비율을 출력, 이때 해당 층의 Frame(F)과 Wall(W) 부재들의 전단력 합은 먼저 모드별로 계산하고 이를 응답스펙트럼의 조합방법에 따라 조합한 값을 사용한다. 따라서, 응답스펙트럼 해석에 대한 밑면전단력은 Numerical Summation에서 출력하는 값을 이용해야 한다.
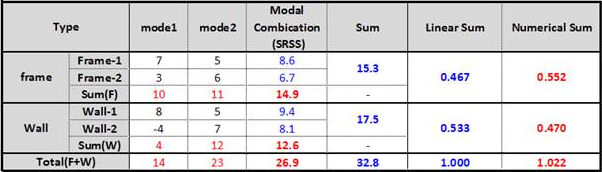
c. LINEAR SUMMATION와 NUMERICAL의 차이 : 아래 표를 통해 예를들면 다음과 같다. Linear Summation은 해당층의 부재들의 전단력의 합을 SRSS조합의 방법으로 구하고, 그 값들을 단순하게 합한 값에 대한 비율을 구한다. 즉, 표에서 해당층의 Frame1과 Frame2의 전단력의 합은 SRSS조합의 방법으로 구한 값으로 각각 8.6(√(7^2+5^2)), 6.7(√(3^2+6^2))이고 frame의 전단력의 합은 두 개를 단순히 더한 값인 15.3이다. Wall도 마찬가지로 Wall-1과 Wall-2의 전단력의 합은 각각 9.4((√(7^2+5^2)), 6.7(√(3^2+6^2))이고 Wall의 전단력의 합은 17.5이다. Frame과 Wall의 Sum의 값 15.3과 17.5를 단순하게 더한 값인 32.8(15.3+17.5)이 해당층의 모든 부재에 대한 Sum의 값으로 이에 대한 Frame과 Wall의 비율이 각각 0.467(15.3/32.8)과 0.533(17.5/32.8)이며 비율의 합은 항상 1이 된다. 이것이 Linear Summation이다. Numerical Summation은 모드별로 해당층의 부재들의 전단력의 값들을 단순하게 더한 값을 구하고, 그 값들을 SRSS조합의 방법으로 각각 계산하여 비율을 구한다. 즉, 표에서 해당층의 모드별(mode1과 mode2) frame 부재의 전단력의 단순합은 각각 10(7+3), 11(5+6)이고, SRSS조합의 방법으로 frame의 전단력의 합을 구하면 14.9(√(10^2+11^2))가 된다. Wall도 동일한 방법으로 구하면 mode1, mode2의 단순합은 각각 4(8-4), 12(5+7)이고, Wall의 전단력의 합은 12.6((√(4^2+12^2))이 된다. 여기서 해당층 모든 부재에 대한 총합은 단순히 14.9와 12.6을 더하는 것이 아니라 각 부재의 모드별 값을 더한 값에 대해 SRSS조합의 방법으로 구하는 것으로 모드별 frame과 Wall의 합인 14(10+4)와 23(11+13)을 SRSS조합의 방법으로 구한 26.9((√(14^2+23^2))가 된다. frame과 Wall의 비율은 각각 0.552(14.9/26.9) 와 0.470(12.6/26.9)이 된다. 이것이 Numerical Summation이다.
|
 버튼을 클릭합니다.
버튼을 클릭합니다.