| 功能说明 |
|
板单元具有单元平面内的三个平动自由度和绕x、y、z轴的三个旋转自由度。
平面板单元的各应变的刚度类型如下:
(1)
面内变形
三节点单元:使用等参单元(与平面应力单元相同),考虑绕z轴的旋转自由度;
四节点单元:使用等参单元(与平面应力单元相同),考虑绕z轴的旋转自由度。
(2)
面外变形:
三节点单元:DKMT
(Discrete Kirchhoff Mindlin Triangle)
四节点单元:DKMQ
(Discrete Kirchhoff Mindlin Quadrilateral)
板的面内刚度需要考虑沿x、y方向的平动位移u、v和绕z轴的旋转位移θz的影响。 |
|
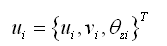 (2.6.2-1) (2.6.2-1) |
|
有N个节点的单元内任意坐标x、y和平动位移u、v使用形函数表示如下: |
|
|
|
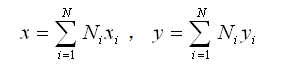 (2.6.2-2) (2.6.2-2) |
|
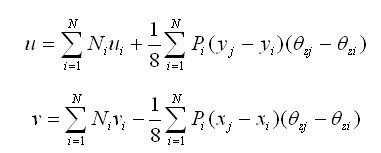
|
|
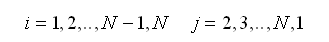 (2.6.2-3) (2.6.2-3) |
|
|
|
其中,θzi是节点上的旋转位移,三节点和四节点板单元的形函数如下:
三节点单元 |
|
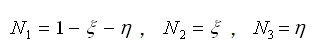 (2.6.2-4) (2.6.2-4) |
|
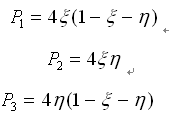 (2.6.2-5) (2.6.2-5) |
|
|
|
四节点单元 |
|
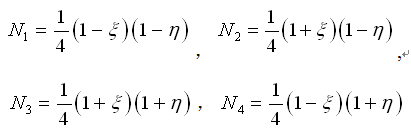 (2.6.2-6) (2.6.2-6)
|
|
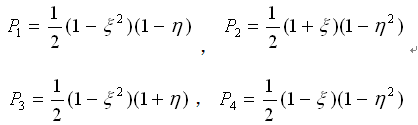 (2.6.2-7) (2.6.2-7)
|
|
|
|
节点位移u和面内应变ε的关系使用转换矩阵Bi表达如下: |
|
|
|
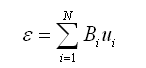 (2.6.2-8) (2.6.2-8) |
|
|
|
转换矩阵Bi用新函数的微分表示如下: |
|
|
|
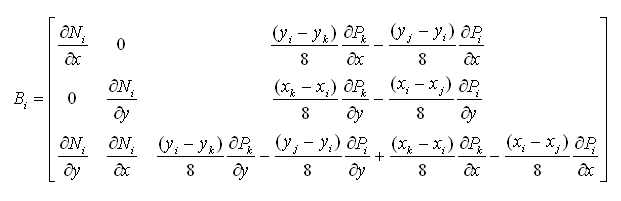
|
|
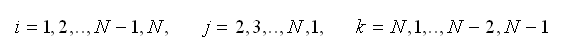 (2.6.2-9) (2.6.2-9)
|
|
|
|
面内变形单元刚度矩阵如下: |
|
|
|
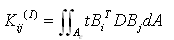 (2.6.2-10) (2.6.2-10) |
|
式中:
|
|
t
 厚度; 厚度;
Ae 面积。 面积。 |
|
各向同性材料的应力和应变关系矩阵D如下: |
|
|
|
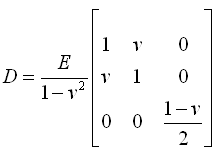 (2.6.2-11) (2.6.2-11) |
|
|
|
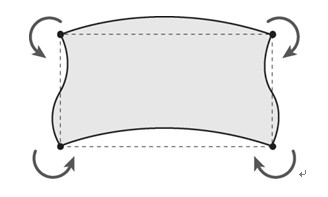
使用具有绕z轴旋转自由度的单元时,在单元的边上会产生附加的平动位移,附加平动位移形状采用二次内插函数,附加变形在节点上不产生剪切变形(见图2.6.2-1): |
|
|
|
|
|
图2.6.2-1 弯曲变形和旋转自由度的关系 |
|
|
|
计算面外刚度使用的DKMT(三节点)和DKMQ(四节点)单元考虑剪切变形的影响,剪切变形采用假想法。节点上的自由度有沿单元坐标系z方向的平动位移ω和绕x、y轴的旋转位移θx、θy:
|
|
|
|
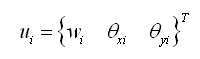 (2.6.2-12) (2.6.2-12) |
|
|
|
平动位移ωi和旋转位移θx、θy用形函数表示如下: |
|
|
|
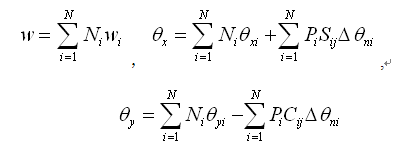 (2.6.2-13) (2.6.2-13)
|
|
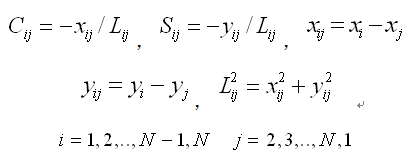
|
|
|
|
其中,形函数Ni 、Np见上面公式(2.6.2-4)~(2.6.2-7)。为了计算单元边上的假想旋转角Δθni使用下列假定:
在N个边上剪力和弯矩满足下列平衡条件: |
|
|
|
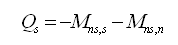 (2.6.2-14) (2.6.2-14) |
|
|
|
绕垂直于单元边的轴的旋转位移沿边长方向为二次函数,绕切线方向轴的旋转位移为一次函数: |
|
|
|
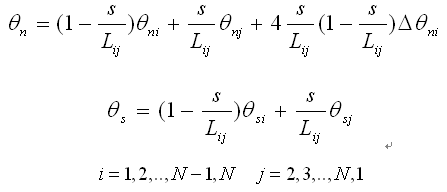 (2.6.2-15) (2.6.2-15)
|
|
|
|
利用式(2.6.2-14)计算的剪切应变γsx和用形函数计算的剪切应变γsx满足下面方程: |
|
|
|
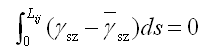 (2.6.2-16) (2.6.2-16) |
|
|
|
将通过上述假定计算的Δθni代入式(2.6.2-13)可得用ui表达的旋转位移θx、θy: |
|
|
|
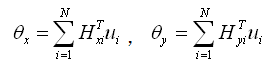 (2.6.2-17) (2.6.2-17) |
|
|
|
其中,Hxi、Hyi分别为: |
|
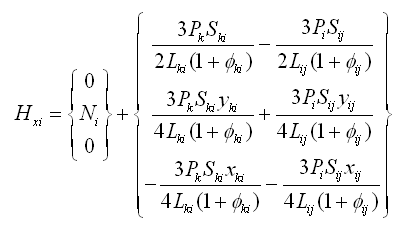 (2.6.2-18) (2.6.2-18)
|
|
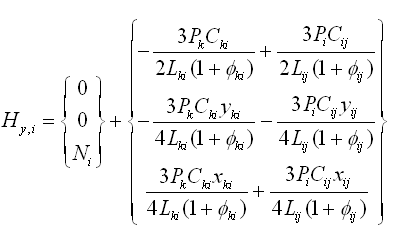 (2.6.2-19) (2.6.2-19)
|
|
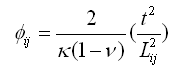 (各向同性材料) (各向同性材料)
|
|
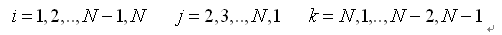
|
|
|
|
节点位移和曲率K的关系如下: |
|
|
|
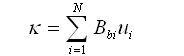 (2.6.2-20) (2.6.2-20) |
|
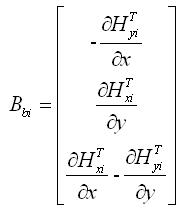 (2.6.2-21) (2.6.2-21) |
|
|
|
剪切变形γ可使用由(2.6.2-16)计算的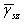 , , |
|
|
|
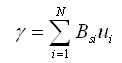 (2.6.2-22) (2.6.2-22) |
|
|
|
其中,剪切变形和节点位移的关系矩阵Bsi如下:
三节点单元: |
|
|
|
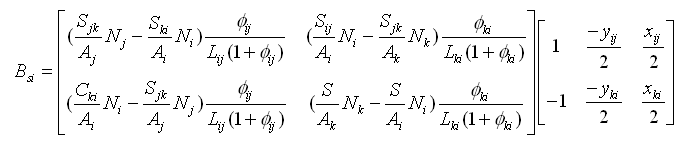
|
|
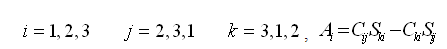 (2.6.2-23) (2.6.2-23)
|
|
|
|
四节点单元: |
|
|
|
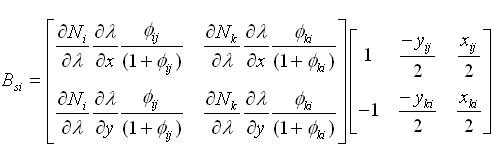 (2.6.2-24) (2.6.2-24)
|
|
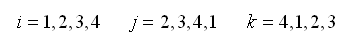
|
|
|
|
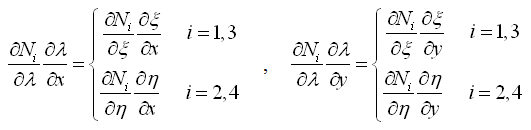 (2.6.2-25) (2.6.2-25)
|
|
|
|
由此可得与面外弯曲和剪切变形相关的刚度矩阵如下: |
|
|
|
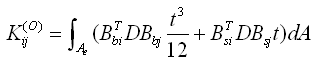 (2.6.2-26) (2.6.2-26) |
|
|
|
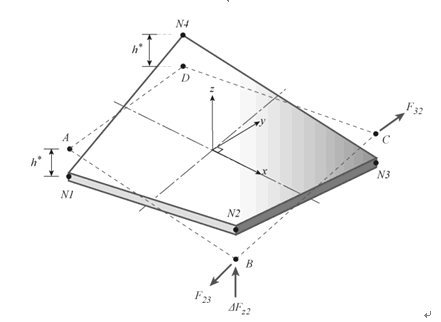
四节点平面板单元的四个节点不在同一个平面时,节点位移会不准确。为了解决这个问题程序使用了MacNeal
推荐的刚度修正法。如图2.6.2-2所示,将在A-B-C-D平面上计算的刚度矩阵Kp转换为实际节点位置N1-N2-N3-N4上的刚度K时使用了转换矩阵S: |
|
|
|
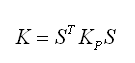 (2.6.2-27) (2.6.2-27) |
|
|
|
|
|
图2.6.2-2
四节点板单元的节点不在同一平面时 |
|
|
|
通过转换矩阵S将点(A-B-C-D)上的荷载Fp转换为点(1-2-3-4)上的荷载F: |
|
|
|
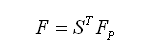 (2.6.2-28) (2.6.2-28) |
|
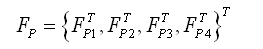 (2.6.2-29) (2.6.2-29) |
|
|
|
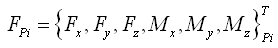 (2.6.2-30) (2.6.2-30) |
|
|
|
转换时由于两个平面的夹角引起的面外荷载和弯矩如下: |
|
|
|
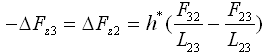 (2.6.2-31) (2.6.2-31) |
|
|
|
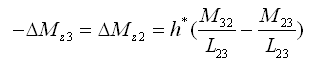 (2.6.2-32) (2.6.2-32) |
|
|
